§ 4.2. Проверка закона распределения.
Предварительный анализ статистических данных заключается в проверке соответствия их предположению о нормальном распределении параметров, для чего строится гистограмма и определяются выборочные числовые характеристики . Для построения гистограммы необходимо выполнить такую последовательность действий:
разместить на рабочем листе Excel статистические данные наблюдений (без выбросов);
Сервис – Анализ данных – Гистограмма (рис.1);
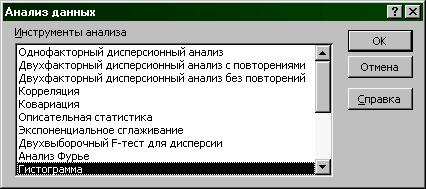
Рис.1.Выбор инструмента анализа.
в появившемся диалоговом окне Гистограмма ввести в поле Входные данные интервал (диапазон) ячеек, содержащий исходные данные, и отметить поле Метки , если таблица данных имеет заголовки;
ввести в поле Параметры выхода адрес ячейки, с которой должны размещаться выходные данные (выходной интервал) и щелкнуть пункт Вывод графика ;
OK.
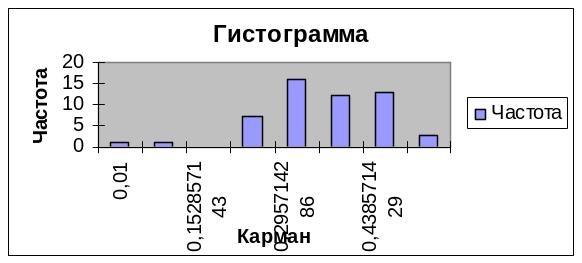
Гистограммы необходимо построить для всех признаков статистических данных и сравнить их с кривой нормального распределения с целью убедиться, что закон распределения каждого признака близок к нормальному, как на приведенной гистограмме.
Числовые характеристики для всех признаков оцениваются по выборке с помощью инструмента анализа Описательная статистика., вызов которого осуществляется аналогично (см. рис.1 ). В появившемся диалоговом окне Описательная статистика необходимо ввести таким же образом Входные данные и Параметры вывода , только вместо пункта Вывод графика следует отметить пункт Итоговая статистика .
Результаты применения инструмента Описательная статистика к данным наблюдений по результативному признаку Y2 и выбранным факторным признакам приведены ниже (Рис.2).
|
Y2 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
|
|
|
|
|
|
Среднее |
86,76959 |
0,316531 |
0,730612 |
0,299592 |
1,321224 |
0,984286 |
Стандартная ошибка |
8,947579 |
0,013529 |
0,007339 |
0,022097 |
0,0173 |
0,066061 |
Медиана |
68,6 |
0,31 |
0,73 |
0,3 |
1,35 |
0,88 |
Мода |
#Н/Д |
0,31 |
0,78 |
0,2 |
1,35 |
0,67 |
Стандартное отклонение |
62,63305 |
0,094705 |
0,051373 |
0,154677 |
0,1211 |
0,46243 |
Дисперсия выборки |
3922,899 |
0,008969 |
0,002639 |
0,023925 |
0,014665 |
0,213842 |
Эксцесс |
0,972081 |
0,898188 |
-0,63168 |
-0,11908 |
-0,62273 |
0,452437 |
Асимметричность |
1,343112 |
-0,25034 |
-0,26748 |
0,228867 |
-0,07536 |
0,622524 |
Интервал |
251,2 |
0,49 |
0,21 |
0,66 |
0,52 |
2,17 |
Минимум |
13,6 |
0,02 |
0,62 |
0,02 |
1,09 |
0,03 |
Максимум |
264,8 |
0,51 |
0,83 |
0,68 |
1,61 |
2,2 |
Сумма |
4251,71 |
15,51 |
35,8 |
14,68 |
64,74 |
48,23 |
Счет |
49 |
49 |
49 |
49 |
49 |
49 |
Рис.2. Описательная статистика
Как видно, результаты Описательной статистики дают возможность оценить справедливость предположения о нормальном распределении признаков: эксцесс и асимметричность невелики, хотя и отличаются от 0. Нормальный закон распределения факторных признаков подтверждается еще и тем, что значения медианы и моды у них совпадают или близки.