§ 3.2. Множественная корреляция

Корреляционная связь между несколькими признаками при k > 2 называется множественной. Простейшим случаем является трехмерная модель. Трехмерная случайная величина (X,Y,Z), распределенная по нормальному закону, характеризуется девятью параметрами:

– математическими ожиданиями Mx, My, Mz ;

– дисперсией Dx, Dy, Dz;

– парными коэффициентами корреляции ρ_xy, ρ_xz, ρ_yz .

Через эти параметры выражаются частные коэффициенты корреляции, которые определяются при фиксированных значениях остальных случайных величин:

Аналогично определяются частные коэффициенты корреляции ρ_xz/y и ρ_yz/x.

Для нормального распределения частный коэффициент корреляции ρ_xy/z совпадает с парным коэффициентом корреляции между X и Y при фиксированном Z в двумерном условном распределении (X,Y)/Z и обладает всеми его свойствами. Частный коэффициент корреляции служит показателем линейной связи между двумя переменными случайными величинами независимо от влияния остальных случайных величин. Для оценки тесноты связи используют и коэффициент детерминации, равный квадрату коэффициента корреляции.

Если частный коэффициент детерминации меньше, чем соответствующий парный коэффициент детерминации, то взаимосвязь между двумя величинами обусловлена частично ( или целиком при равенстве нулю частного коэффициента детерминации ) воздействием на эту пару остальных, фиксируемых, случайных величин. Если же, наоборот, частный коэффициент детерминации больше соответствующего парного коэффициента детерминации, то фиксируемые величины ослабляют связь.

Множественный коэффициент корреляции между одной величиной Z и двумя другими величинами (X,Y) определяется по формуле:

и является мерой связи между одной случайной величиной и двумя остальными. Множественный коэффициент детерминации, равный , показывает долю дисперсии случайной величины Z , обусловленную изменением случайных величин (X,Y).

Значения множественного коэффициента корреляции заключены между 0 и 1: 0 ≤ ρ_z≤ 1. При ρ_z = 1 связь между Z и (X,Y) является функциональной. Точки (x,y,z) расположены в плоскости регрессии Z на (X,Y) . Если ρ_z = 0 , то одномерная случайная величина Z и двумерная случайная ве личина (X,Y) являются независимыми ( в силу нормальности их распределения). При этом .

В случае многомерной модели случайной величины особое значение имеют условные распределения. Для трехмерной модели это – условное распределение при фиксированном z и условное распределение при заданном (x,y).

При заданном z получаем двумерное распределение (x,y)/z, которое определяется при нормальном распределении пятью параметрами: двумя условными математическими ожиданиями μ_x/z и μ_y/z ; двумя условными дисперсиями σ²_x/z и σ²_y/z ; условным коэффициентом корреляции ρ_xy/z.

Распределение z/(x,y) является одномерным и определяется своими условным математическим ожиданием Mz/(x,y) и условной дисперсией Dz/(x,y) = σ²_z/xy. Если точку (x,y) менять, то получим плоскость регрессии z на (x,y)

Mz/(x,y) – μ_z = β_zx/y(x – μ_x) + β_zy/x(y – μ_y)

и остаточную дисперсию относительно плоскости регрессии, совпадающую с условной дисперсией

σ²_z/xy = σ²_z/x(1 – ρ²_zx/y) = σ²_z/x(1 – ρ²_yz/x) .

β_zx/y и β_zy/x – коэффициенты множественной регрессии. Множественный коэффициент корреляции ρ_z можно вычислить в силу линейности регрессии и как корреляционное отношение z на (x,y):

Точечные оценки частных и множественных коэффициентов корреляции вычисляются по выборке и выражаются через оценки основных числовых характеристик. Оценками математических ожиданий служат выборочные средние :

Оценки дисперсий – выборочные дисперсии:

,

где S_x , S_y , S_z – оценки средних квадратических отклонений.

Оценки парных коэффициентов корреляции :

r_xz и r_yz определяются аналогично.

Оценка частного коэффициента корреляции:

( аналогично для всех остальных).

Оценки условных средних квадратических отклонений :

Оценки множественных коэффициентов корреляции:

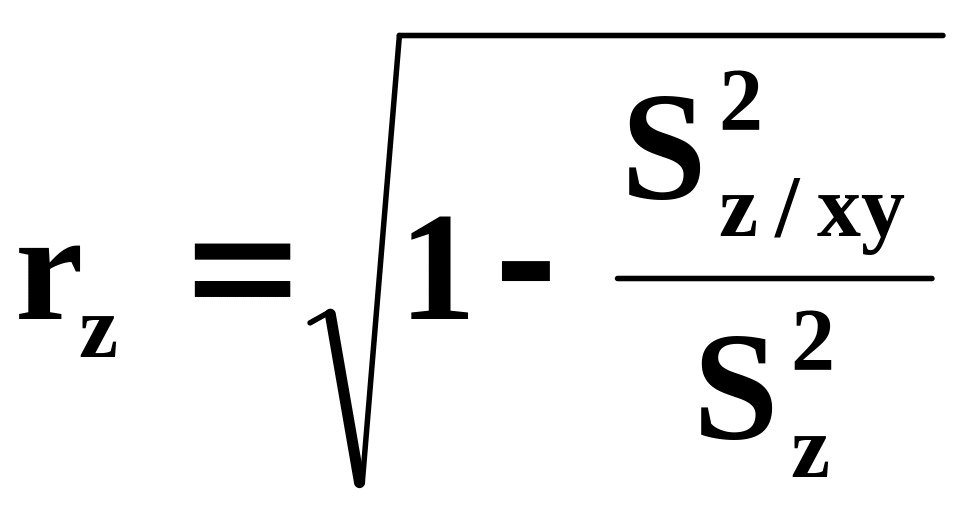
Проверка значимости множественного коэффициента детерминации ρ_z² осуществляется с помощью F-распределения. Вычисляется

F_набл =

Затем с уровнем значимости α и числами степеней свободы ν₁=2 (числителя ) и ν₂ = n – 3 (знаменателя) находят F_кр. Если F_набл > F_кр , гипотеза H₀ : ρ_z² = 0 отвергается с вероятностью ошибки α, т.е. ρ_z² значимо отличается от 0. В противном случае, если коэффициент ρ_z незначим, связь между случайной величиной Z и случайной величиной (X,Y) отсутствует.

Для значимых множественных коэффициентов корреляции можно получить оценки уравнения регрессии. Так, если ρ_z значимо отличается от нуля, оценкой соответствующего уравнения регрессии будет

.

При этом коэффициенты регрессии вычисляются по формулам:

и является оценкой Mz/(x,y).

Для значимых параметров связи можно найти интервальную оценку с надежностью γ = 1 – α с помощью Z–преобразования Фишера.