1.8.4 Момент пары сил относительно оси

         Момент пары, как вектор, направлен перпендикулярно плоскости действия пары в ту сторону, откуда вращение тела парой сил представляется происходящим против направления вращения часовой стрелки.

Рисунок 1.17 Момент пары сил

Так как пару сил можно переносить в ее плоскости действия и в любую другую плоскость, ей параллельную, то ее момент не имеет определенной точки приложения и является свободным вектором. Такие векторы можно переносить параллельно самим себе в любую точку тела.

Модуль момента пары сил равен произведению модуля одной из сил пары на ее плечо. Значение момента пары сил можно также находить как момент одной из сил пары относительно точки приложения другой силы.

При определении момента пары сил относительно какой-либо оси достаточно найти проекцию вектора-момента этой пары на данную ось. На рисунке момент пары сил относительно осей будет равен:

 

М_1х = 0;  М_1у = М₁;  М_1z = 0;

1.8.5 Порядок решения задач на произвольную пространственную систему сил

В заданиях к расчетно-графической работе на данную тему, как правило, требуется определить реакции опор. Задачи такого типа можно решать в следующей последовательности.

1. Устанавливаем тело, равновесие которого будем рассматривать.

2. Определяем виды связей, наложенных на тело и их реакции.

3. Составляем расчетную схему, на которой связи заменяем реакциями, а также показываем все заданные силы и геометрические размеры.

4. Составляем шесть уравнений равновесия и, решая их, находим неизвестные величины.

1.8.6 Пример выполнения расчетно-графической работы «Определение реакций опор твердого тела»

Квадратная плита (рис. 1.18) весом 200 Н горизонтально крепится к стене в точках А и В, а снизу опирается на стержень СD. На плиту действует пара сил.

Рисунок 1.18

Известно, что F=180 Н, KL=KN=0,6м; =70; a=0,8м; b=1м; c=0,4 м; F || x, LN  x. Определить реакции опор конструкции.

Дано: P=200 Н, F=180 Н, KL=KN=0,6м; =70; a=0,8м; b=1м; c=0,4 м; F || x, LNx

Найти X_A, Y_A, Z_A, Z_B, X_B, S

Решение.

Рассмотрим равновесие данной конструкции. Конструкция находится в равновесии под действием приложенных сил – веса P, пары сил и реакций связей. Пару сил можно показать на расчетной схеме в виде вектора момента M, модуль которого будет равен М= F∙h = F∙LN =180∙1.2=216 Нм.

На конструкцию наложены следующие связи: в точке А – сферический шарнир, в точке В – цилиндрический шарнир и в точке С – стержень. Составим расчетную схему, на которой покажем заданные силы: вес плиты P, пару сил с моментом М. Освободимся от связей, заменив их на расчетной схеме реакциями: сферический шарнир в точке А заменим составляющими реакции шарнира X_A, Y_A, Z_A, цилиндрический шарнир В – составляющими Z_B, X_B, реакцию стержня S направим вдоль стержня вниз, предполагая, что стержень растянут. Реакцию стержня S представим в виде проекций на координатные оси:

S_X= -S∙cos30, S_Z= -S∙sin30

При определении момента пары сил относительно какой-либо оси достаточно найти проекцию вектора-момента этой пары на данную ось:

М_Z=M∙sin20=216∙sin20=73,88 Нм,

М_Y=M∙cos20=216∙cos20=202,97 Нм

Рисунок 1.19 – Расчетная схема к задаче

Чтобы было удобно составлять уравнения равновесия, можно составить для каждой из трех плоскостей (ZX, ZY, XY) свою расчетную схему. При составлении расчетной схемы для каждой плоскости взгляд направляем со стороны положительного отсчета каждой оси.

Построим расчетную схему для плоскости ZY. При построении смотрим с конца оси x. На расчетной схеме вначале изображаем координатные оси z и y. Затем, в точках А и В показываем реакции Y_A, Z_A, Z_B. По центру плиты изображаем вес Р. В точке С показываем проекцию силы S на ось z. Пара сил относительно оси x момента не создает, так как F||x, реакции X_A, X_B на плоскость ZY проецируются в точку, поэтому на схеме их не показываем.

Рисунок 1.20 – Расчетная схема в плоскости ZY

Условия равновесия для полученной пространственной системы сил состоят из шести уравнений равновесия. По данной расчетной схеме можно составить три уравнения равновесия:

(1.17)

(1.18)

(1.19)

Рассмотрим плоскость XY. Составим расчетную схему, смотрим со стороны оси z. Покажем силы, которые проецируются на плоскость XY.

Рисунок 1.21 – Расчетная схема в плоскости XY

Момент пары сил М_z покажем дуговой стрелкой. Составим два уравнения равновесия.

(1.20)

(1.21)

Рассмотрим плоскость ZX. Составим расчетную схему и запишем уравнение равновесия.

Рисунок 1.22 – Расчетная схема в плоскости ZX

(1.22)

Определим неизвестные величины. Из уравнения (1.22) найдем реакцию стержня S.

Знак «минус» означает, что стержень СD сжат.

Из уравнения (1.21) найдем реакцию X_B.

Из уравнения (1.20) найдем реакцию X_А.

Из уравнения (1.19) найдем Z_В.

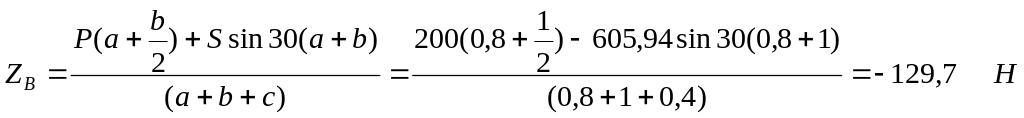
Из уравнения (1.18) найдем Z_А.

Из уравнения (1.17) следует, что Y_A=0.

Знак «минус», стоящий перед реакциями X_A, Z_B, X_B, означает, что реакции направлены в противоположную сторону.

Чтобы убедиться, что реакции найдены правильно, выполним проверку. Составим уравнение моментов относительно оси, проходящей через точку О на рисунке 1.23. Положение точки О выбираем так, чтобы в уравнении моментов присутствовали моменты от всех найденных неизвестных реакций. Размер d назначим произвольно и примем его равным 0,5 м.

Рисунок 1.23 – Расчетная схема для выполнения проверки

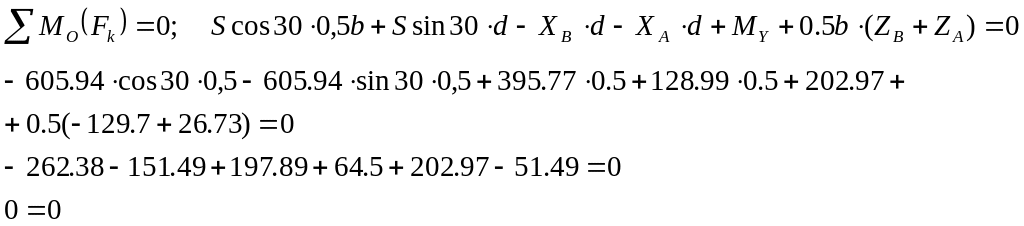Равенство выполняется, значит, реакции определены, верно.

Ответ: X_A=-128,99 Н, Y_A= 0 Н, Z_A=26,73 Н, Z_B=-129,7 Н, X_B=-395,77 Н,

S=-605,94 Н.