1.6 Условие равновесия произвольной плоской системы сил

Произвольной плоской системой сил называется система сил, линии действия которых лежат в одной плоскости и не пересекаются в одной точке.

Очевидно, что для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и её главный момент относительно любого центра А были равны нулю:

(1.6)

Векторные уравнения (1.6) можно записать тремя системами уравнений равновесия произвольной плоской системы сил:

; ;

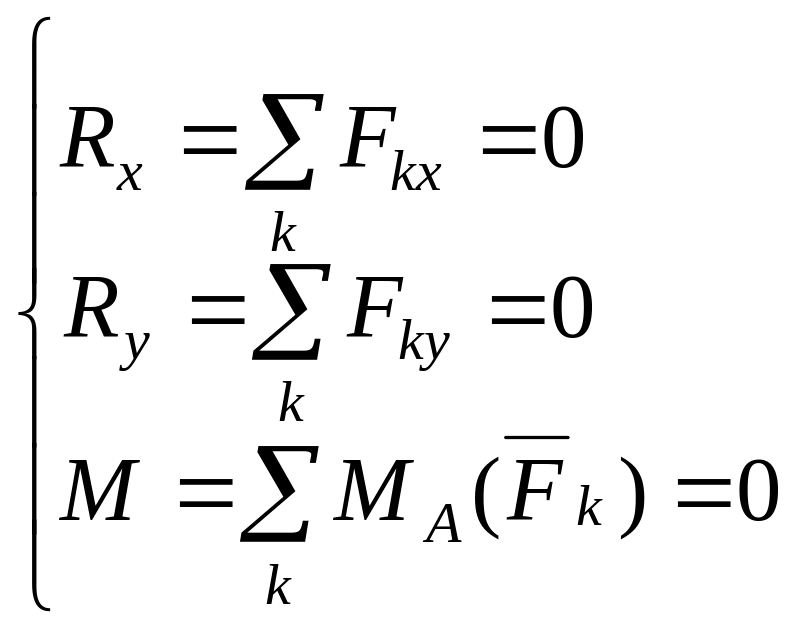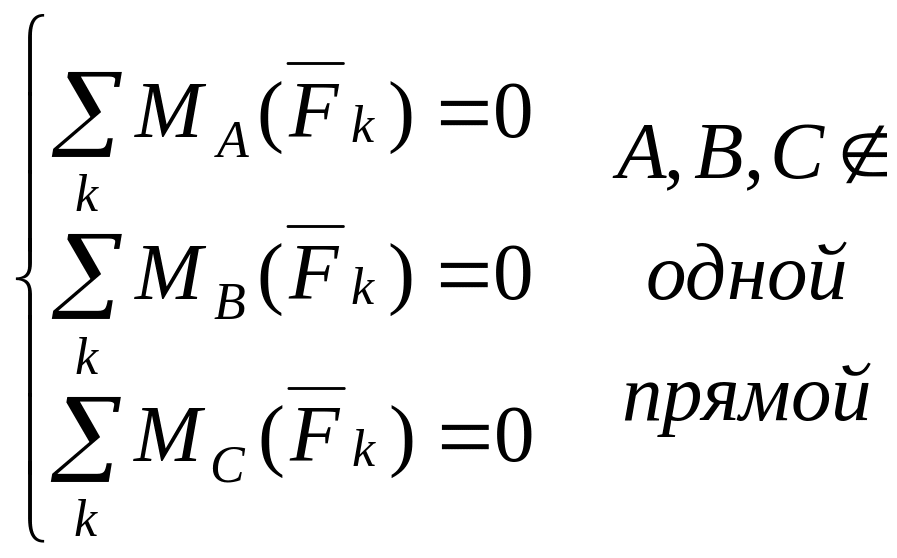
1.7 Пример выполнения расчетно-графической работы «Определение реакций опор составной конструкции»

Дано: F₁ =10 кН, М =30 кНм, q=5 кН/м.

Определить реакции опор в точках А и В, реакцию соединения в точке С.

Рисунок 1.9 – Схема конструкции

Решение.

1. Шарнирное соединение в точке С.

Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня СВ, к которому приложено наименьшее число неизвестных сил. Составим расчетную схему стержня, на которой покажем заданную силу F₁, момент М и реакции связей. Проведем оси координат хy. Силу F₁ спроецируем на координатные оси и покажем ее проекции на схеме. Реакцию шарнира С покажем в виде двух составляющих Х_С и Y_С. Подвижный шарнир в точке В заменим реакцией R_B, которую направим вверх. Для полученной произвольной плоской системы сил (рис. 1.10) составим три уравнения равновесия:

Рисунок 1.10 – Расчетная схема стержня СВ

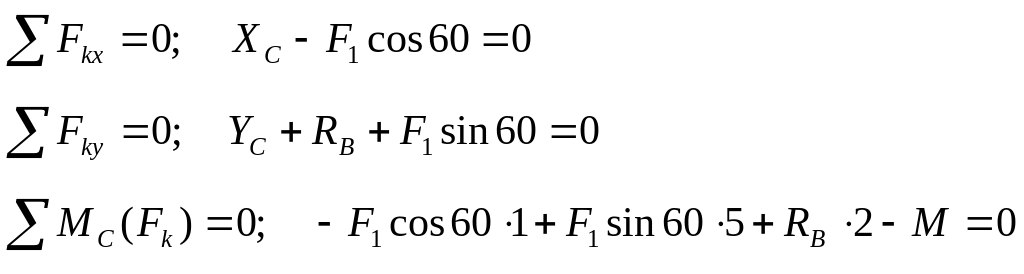
Подставив, в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

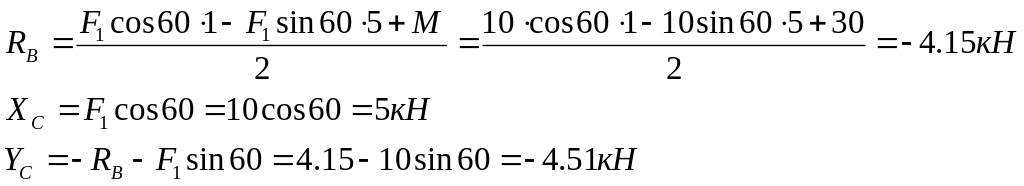
Для определения реакций в точке А рассмотрим равновесие всей конструкции в целом. Составим расчетную схему, на которой покажем заданные силы и реакции связей. Распределенную нагрузку интесивностью q заменим сосредоточенной силой Q, модуль которой определим по формуле . Силу приложим по центру участка. Реакцию жесткой заделки в точке А покажем двумя составляющими Х_А и Y_А, здесь же покажем момент М_А.

Рисунок 1.11 – Расчетная схема конструкции

Для полученной произвольной плоской системы сил (рис. 1.11) составим три уравнения равновесия:

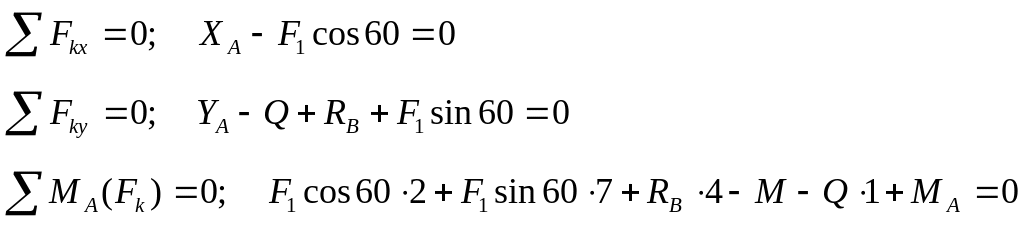
Подставив, в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

Для проверки найденных реакций составим уравнение моментов для всей конструкции (рис.4) относительно точки С.

Равенство выполняется, значит, реакции найдены, верно.

2. Скользящая заделка в точке С

Рисунок 1.12 – Схема конструкции

Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня СВ, к которому приложено наименьшее число неизвестных сил. Составим расчетную схему стержня, на которой покажем заданную силу F₁, момент М и реакции связей. Проведем оси координат хy. Силу F₁ спроецируем на координатные оси и покажем ее проекции на схеме. Реакцию Х_С скользящей заделки С направим горизонтально. Подвижный шарнир в точке В заменим реакцией R_B, которую направим вверх. Для полученной произвольной плоской системы сил (рис. 1.13) составим уравнения равновесия:

Рисунок 1.13 – Расчетная схема стержня СВ

Подставив, в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

Для определения реакций в точке А рассмотрим равновесие всей конструкции в целом. Составим расчетную схему, на которой покажем заданные силы и реакции связей. Распределенную нагрузку интенсивностью q заменим сосредоточенной силой Q, модуль которой определим по формуле . Силу приложим по центру участка. Реакцию жесткой заделки в точке А покажем двумя составляющими Х_А и Y_А, здесь же покажем момент М_А.

Рисунок 1.14 – Расчетная схема конструкции

Для полученной произвольной плоской системы сил (рис. 1.14) останутся в силе уравнения к рисунку 1.11:

Подставив, в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

Для проверки найденных реакций составим уравнение моментов для всей конструкции (рис. 1.14) относительно точки С.

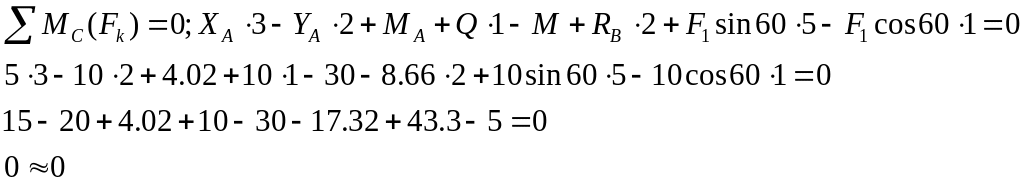
Равенство выполняется, значит, реакции найдены, верно.

Результаты расчета приведены в таблице 1.

Таблица 1.1

Тип соединения	Реакции, кН					Моменты, кНм
	ХА	YA	RB	XC	YC	МА	МС
Соединение шарниром	5	5,49	-4,15	5	-4,51	-14,02	-
Соединение скользящей заделкой	5	10	-8,66	5	-	4,02	9,02