2.3 Определение ускорений точек тела при плоскопараллельном движении

Для определения ускорения точки М воспользуемся формулой (2.4). Выберем за полюс точку А тела и будем определять ускорение произвольной точки М:

.

Продифференцируем это равенство по времени:

. (2.10)

(2.11)

Ускорение - это ускорение точки М при вращении тела вокруг полюса А с угловой скоростью ω и угловым ускорением ε. Оно определяется согласно теории вращательного движения тела по формуле:

, где , . (2.12)

Модуль вектора определяется по формуле

=МА . (2.13)

Угол μ (рисунок 2.11) между направлением и прямой МА определяется по формуле

tgμ = ε/ω². (2.14)

Вектор направлен из точки М к полюсу А; вектор направлен перпендикулярно МА в сторону, согласованную с направлением углового ускорения тела ε.

Рисунок 2.11 – Определение ускорения произвольной точки М

Точка А, выбранная нами за полюс, в общем случае криволинейного движения имеет ускорение, определяющееся по двум составляющим:

. (2.15)

Таким образом, ускорение произвольной точки М можно определить, зная ускорение другой точки тела, выбираемой за полюс, по формуле:

. (2.16)

Ускорение точки М тела можно определить также и используя формулу (2.5): V_M = ωMP.

Продифференцируем равенство (2.5) по времени, получим:

. (2.17)

В этой формуле производная правой части определяется как производная от произведения функций, зависящих от времени, так как с течением времени меняется и угловая скорость и расстояние точки до мгновенного центра скоростей МР.

- угловое ускорение точки в данный момент времени;

- неизвестная величина, так как неизвестна функция изменения расстояния МР с течением времени. Таким образом, формула (2.17) имеет смысл, если = 0, то есть когда расстояние точки до мгновенного центра скоростей остается постоянным. Это происходит в случае качения диска по неподвижной поверхности, если точка М - центр диска. Тогда

(2.18)

- ускорение центра диска при его качении по прямолинейной поверхности (рис. 2.12,а ).

Рисунок 2.12 – Ускорение центра диска в случаях прямолинейного (а) и криволинейного (б) движения

В случае качения диска по криволинейной поверхности ускорение центра диска определяется по формулам (рис. 2.12,б):

, (2.19)

, где - радиус кривизны дуги, описываемой точкой М.

Аналогично понятию «мгновенный центр скоростей» на плоскости в каждый момент времени есть точка Q, называемая мгновенным центром ускорений, характеризуемая тем, что ее ускорение в данный момент времени равно нулю. Эту точку можно найти, если известно ускорение какой-либо точки А тела и величины углового ускорения ε и угловой скорости ω тела в данный момент времени.

Для построения точки Q надо (см. рис. 2.13):

1. найти значение угла μ из выражения ;

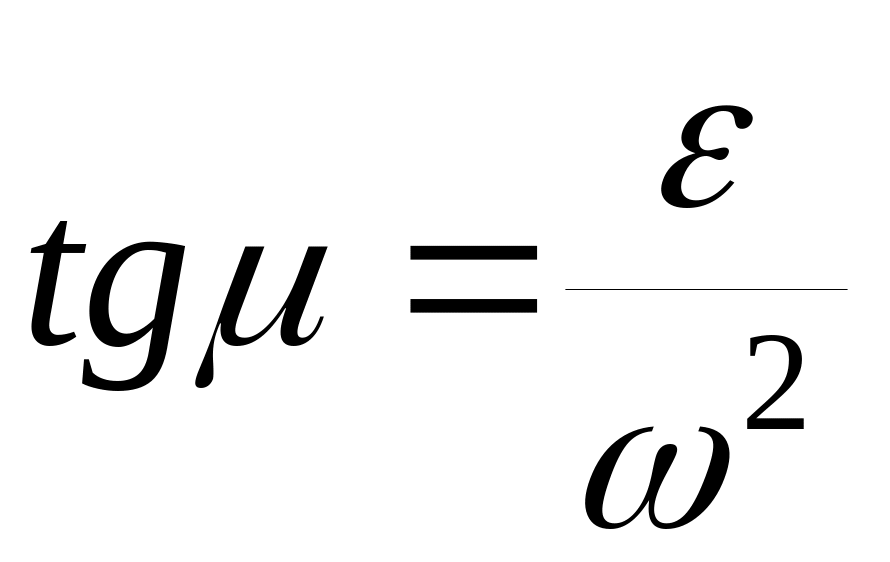2. начертить на плоскости известное ускорение и от точки А под углом μ, отклоненным от вектора в направлении ε, провести прямую АЕ;

3. отложить от точки А вдоль прямой АЕ отрезок АQ, равный

. (2.20)

Найденная таким образом точка Q и является мгновенным центром ускорения. Проверим это. Для проверки найдем ускорение точки Q, .

, где .

Рисунок 2.13 – Определение положения мгновенного центра ускорений

Вектор образует с прямой AQ угол μ (так как это ускорение точки Q вокруг полюса А, см. формулы 2.12-2.14), поэтому ║ . По направлению эти векторы противоположны. Тогда имеем:

.

Итак, утверждение доказано.

Если точку Q принять за полюс при определении ускорения какой-либо точки М или точки К, то

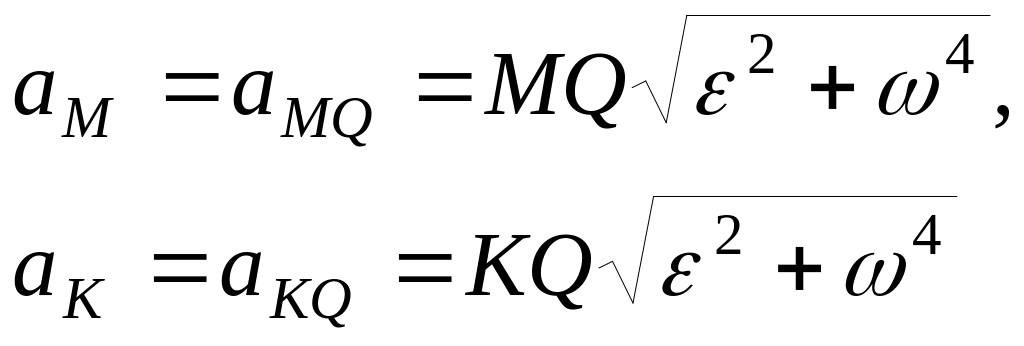(2.21)

Из полученных выражений следует, что

. (2.22)

Углы, образуемые векторами ускорений точек с отрезками, соединяющими точки с центром Q, равны μ. Поэтому ускорения всех точек фигуры в данный момент времени распределены так, как если бы тело вращалось вокруг центра Q как неподвижного (см. рис. 2.14).

Рисунок 2.14 – Распределение ускорений точек плоской фигуры относительно мгновенного центра ускорений

Следует помнить, что мгновенный центр скоростей Р и мгновенный центр ускорений Q – это две разные точки плоскости. Совпадают они только при вращении фигуры вокруг неподвижного центра, а в общем случае

(2.23)