Корпускулярно-хвильовий дуалізм нанооб'єктів

Як відомо, світло є одночасно частинкою і хвилею. У 1924 році французький вчений Шарль де Бройль запропонував принцип корпускулярно-хвильового дуалізму на всі мікрообєкти природи. Згідно де Бройлю, кожній частинці відповідає хвиля, довжина якої пов'язана з імпульсом цієї частинки. По де Брой-левській гіпотезі про загальність корпускулярно-хвильового дуалізму, не лише фотони, але і усі частки взагалі (електрони, протони і так далі) разом з корпускулярними мають також хвильові властивості. Останні, у свою чергу, повинні проявлятися в явищах дифракціі і інтерференції. Коли вивчають світло, спочатку впадають у вічі його хвильові властивості, а при детальнішому розгляді - корпускулярні. Відповідно до відомого співвідношення Айнштайна, фотону з енергією E = h∙v, відповідає енергія Е = mc²=h∙v, де с − швидкість світла; т − маса фотона; v − його частота. Звідси:

Враховуючи, що імпульс фотона p = m∙c, а частота світла пов'язана з довжиною хвилі λ співвідношенням: , отримаємо: . Це рівняння є ілюстрацією подвійної природи світла, оскільки об'єднує довжину хвилі світла λ, пов'язану з його хвильовою природою, і імпульс фотона р, що характеризує його як частинку. Заслуга де Бройля полягає в тому, що він розповсюдив цю фор-мулу на усі частки матерії, надавши їй універсальне значення

де p = m∙v - імпульс частки, m - маса частки, v - її швидкість. Гіпотеза де Бройля згодом була підтверджена экспериментально. Зокрема, в досвіді американських фізиків К. Девідсона і Л. Джермера в 1927 році виявлена дифракція елементарних частинок - електронів. Для цього вони використали відому електронно-променеву трубку, що застосовується в телевізорах, дисплеях і осцил-лографах. У цих трубках (чи електронних гарматах) електронні пучки, генеровані катодом і керовані електромагнітним полем, направляются у бік екрану, покритого люмінофором. При попаданні частки в екран на ньому виникає плямочка, що світиться, тобто на шляху від джерела до екрану електрони поводяться як класичні частки, і їх рух можна розрахувати засобами класичної фізики. Проте якщо на шляху електронів, що летять в трубці, поставити екран з щілиною, то після проходження їх через цю щілину на екрані спостерігається чергування темних і світлих смуг, аналогічне дифракційній картині світлових хвиль. Значить, електрони здатні до дифракції, тобто поводяться подібно до хвиль.

Пізніше вчений Тартаковский довів, що хвильові властивості властиві не лише пучкам електронів, але і кожному електрону окремо. А в 1999 році виявлена інтерференція фулеренів і біомолекул. Довжина хвилі де Бройля обернено пропорційна до імпульсу частинки. Фактично це означає, що для великих важких часток довжина хвилі, що виникає при їх русі, дуже мала, і хвильові властивості таких часток помітити практично неможливо. Це стосується усіх макрооб'єктів, для більш-менш точного опису яких, цілком вистачає класичної механіки.

Квантові межі точності вимірів

Однією з актуальних проблем сучасної нанотехнології є так звана ―проблема «товстих пальців», під якою мається на увазі складність маніпулювання мікро- і наночастинками.

Нільс Бор сформулював один із засадничих принципів квантової механіки - принцип доповненості, згідно якому неможливо точно виміряти одну фізичну величину мікрообєкта без втрати інформації про її додаткову величину.

Фактично суть таких взаємно додаткових величин описується і співвідношенням невизначеності Гейзенберга, яке твердить, що існують такі пари фізичних величин, одночасне і точне визначення яких неможливе. Прикладом такої пари величин є координати частки х і проекція її імпульсу р на вісь х. Кількісно співвідношенням невизначеності формулюється таким чином: якщо Δх-невизначеність координати частки, а Δр- невизначеність проекції імпульсу частки р на вісь x, то їх добуток має бути не менший постійної Планка h : .

Звідси витікає, що якщо точно визначити координату частки, то нічого не можна сказати про її імпульс і навпаки. Із співвідношення невизначеності виходить, що чим точніше встановлене значення однієї з величин, що входить в нього, тим менш точно визначене значення іншої. Інша пара величин, пов'язаних співвідношенням невизначеності, - це енергія системи Е і час t, впродовж якого система має це значення енергії. В цьому випадку співвідношення невизначеності виглядає так: ΔE∙Δt ~h. Звідси витікає, що якщо є можливість спостерігати динамічну систему впродовж часу Δt, то її енергія може бути визначена з точністю, не більше, ніж : .

Таким чином, принцип невизначеності встановлює фундаментальні, принципово непереборні межі точності вимірів.

Принцип невизначеності часто пояснюють впливом вимірювального приладу на частки. Із-за недосконалості вимірювальних приладів не можна точно вказати місце розташування частки в деякому об'ємі dV, а можна лише вказати вірогідність dP його місцезнаходження в тій або іншій частині об'єму dV. Ця вірогідність dP прямо пропорційна dV і пов'язана з нею наступним співвідношенням: .

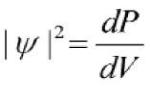Таким чином, вірогідність знаходження частки в деякий момент часу t в деякому об'ємі dV, тобто фактично місце її знаходження в точці з координатами x, y, z, визначає квадрат модуля деякої функції ψ (псі). Ця функція носить назву хвильової і саме вона описує рух елементарних часток, який носить імовірнісний характер. Щоб визначити хвильову функцію частки, фізики вирішують рівняння Шрьодінгера, яке враховує вплив електромагнітних сил на її рух. Воно є диференціальним рівнянням похідних другого порядку : .

У цьому рівнянні m - маса електрона, E і V - відповідно повна і потенційна енергії частки; псі - хвилева функція трьох просторових координат. Фізичний сенс величини псі - полягає в тому, що квадрат її характеризує вірогідність знаходження електрона в цій точці. Или, інакше: dV 2  є мірою електронної щільності в об'ємі dV. Найважливішою властивістю рівняння Шрьодінгера є те, що воно має розвязок тільки для ряду дискретних значень енергії E . Найбільш простий ряд таких значень рівняння Шрьодінгера дозволяє отримати для атома водню, що складається з одного протона і одного електрона.

Потенціальна енергія системи, що складається з одного протона із зарядом + e і одного електрона із зарядом, - е, що знаходиться від протона на відстані r, може бути представлена виразом .

Якщо підставити цей вираз в рівняння Шрьодінгера і вирішити його, то буде отриманий ряд значень енергії, який може бути представлений рівнянням: , де n так зване головне квантове число рівне I, 2, 3,...∞. Отриманий ряд значень енергії може бути представлений схематично у вигляді набору енергетичних рівнів атома водню. Енергетичні переходи електрона з одного рівня енергії на іншій відповідають тим або іншим спектральним лініям атомарного водню, спостережуваним експериментально, в ультрафіолетовій видимій або інфрачервоній областях випромінювання; довжина хвилі спектральних ліній може бути вичислена по формулі Планка : .

Квантові розмірні ефекти

На ввідній лекції було дано поняття ультрадисперсності і показано, що зі зменшенням розміру часток якої-небудь речовини його фізичні і хімічні властивості можуть істотно мінятися. Це відбувається через те, що хід фізичних процесів залежить не тільки від властивостей самої речовини, але і від геометрії тієї області простору, в якій вони протікають, тобто від ―розмірів цієї області. Для наочної ілюстрації цієї ідеї приведемо наступну аналогію: уявимо, що у вузькому провулку треба розгорнутися якомусь транспортному засобу. Очевидно, що мотоциклістові це буде зробити легше, ніж водієві тяжѐлоготипу КАМАЗа.

Розмірні ефекти в твердих тілах - це явище, яке спостерігається при умовах, коли геометричні розміри об'єкту порівнянні з тією або іншою з довжин, що визначають протікання фізичних процесів (наприклад, завдовжки вільного пробігу носія заряду, завдовжки хвилі де Бройля і так далі). Залежно від розмірів досліджуваного зразка розрізняють класичні і квантові розмірні ефекти, які можуть впливати практично на будь-які властивості речовини. Зрозуміло, що для нанометрових об'єктів, де розміри часток співмірні з де Бройлівской довжиною хвилі електрона, характерні саме кван-товые розмірні ефекти, визначальні такі властивості речовини, як теплоємність, електропровідність деякі оптичні свойст-ва і тому подібне. Найяскравішим представником квантових розмірних ефектів є тунельний ефект - явище, що відіграє важливу роль в нанотехнології. Суть тунельного ефекту була розглянута раніше. Це явище чисто квантове, адже класична частка не може знаходитися усередині потенційного бар'єру висоти V, якщо її енергія E<V, оскільки кінетична енергія частки стає при цьому негативною, а її імпульс - уявною величиною.

Рис.2.1 Умовна схема тунельного переходу

Проте для мікрочастки це виведення не справедливе: внаслідок співвідношення невизначеності фіксація частки усередині бар'єру робить невизначеним її імпульс. Оскільки потенційна енергія частки однозначно визначається її координатою, кінетична енергія − імпульсом, а в силу співвідношення невизначеності, одночасно і точно координату і імпульс частки визначити неможливо, те розділення енергії на кінетичну і потенційну в квантовій фізиці безглуздо. Відповідно, з'являється вірогідність проходження частки крізь потенційний бар'єр. Феномен туннелювання відкрив в 1928 році Г. А. Гамов, уперше отримавши розвязок рівняння Шрьодінгера, яке описує можливість подолання, частинкою енергетичного бар'єру, навіть якщо її енергія менша за висоту бар'єру. Знайдений розвязок пояснив багато процесів, що спостерігалися експериментально, і дозволив зрозуміти велике коло явищ, що відбуваються при вильоті частинки з ядра - основи атомної науки і техніки. І лише через тридцять років після відкриття Гамова з'явилися перші прилади на основі тунельного ефекту: тунельні діоди, тран-зисторы, датчики, термометри для виміру наднизьких темпера-тур, і, нарешті, скануючі тунельні мікроскопи, що започаткували сучасну нанотехнологію.

У квантовій механіці широко використовується принцип суперпозиції. Це означає, що результат дії двох або більше хвиль може бути отриманий сумованням окремих хвиль. Відповідно до цього припущення, якщо квантово-механічна система може знаходитися в декількох станах, що описуються, відповідно, хвилевими функціями ψ1, ψ2, ψ3. ψn, то фізично допустимою буде і суперпозиція (підсумовування, аддитивність) цих станів, тобто стан, що зображується хвилевою функцією .

де c1, c2, c3.,cn - вірогідність знаходження системи в станах ψ1, ψ2, ψ3. ψn відповідно. Таким чином, будь-яка складна хвильова функція може бути представлена у вигляді сукупності декількох простіших функцій. Можливість станів, в яких ця фізична ве-личина не має певного значення, а визначається суперпози-цией вірогідних станів цієї величини, є характерною рисою квантової механіки, яка принципово відрізняється її від класичної меха-ники. Описати такий ―змішаний стан однієї час-тинки на мові класичної механіки неможливо, тому помилково розглядати (навіть теоретично) фізичні системи, в яких формально об'єднані як класичні, так і квантові объ-екты, оскільки такі системи некоректні для дослідження - в них виявляються протиріччя, які не можливо розвізати.

Квантові точки, дроти і площини

Одне з промислових застосувань нанотехнологій пов'язане з квантовими точками і площинами.

Квантова площина - це багатошарова твердотіла струк-тура з тонких плівок різних речовин завтовшки в один атом, складених одна на одну. Із-за малої товщини плівок в таких структурах починають проявлятися квантові ефекти, які дуже сильно впливають на поведінку електронів усередині квантової площини, що дозволяє довільним чином міняти физичні і хімічні властивості таких речовин.

Перший етап нового напряму, що відкриває широкі пер-спективы. Квантові точки - це крихітні пірамідки в 50-100 атомів одного матеріалу, розміщених на монокристалі іншого матеріалу.

Рис.2.2 Квантова точка

Піонером в області створення приладів на таких структурах був російський учений, академік Жорес Іванович Алферов, що став в 2002 році Нобелівським лауреатом. Услід за Нобелівською премією Алфе-ров отримав і державну. Його робота ―Фундаментальні ис-следования процесів формування і властивостей гетероструктур з квантовими точками і створення лазерів на їх основі ознаменувала розмір однієї квантової точки складає одиниці-десятки нанометрів. Електронний спектр ідеальної квантової точки відповідає електронному спектру поодинокого атома, хоча реальний квантовий об'єкт при цьому може складатися з сотень тисяч атомів. Саме з цієї причини квантові точки називають також ―штучними атомами.

Зважаючи на малу величину квантової точки, на її основі можна будувати різні напівпровідникові пристрої, що використовують у своїй роботі квантові розмірні ефекти. Лазери нового покоління, грунтовані на гетероструктурах з квантовими точками, прекрасно працюють, підтверджуючи стару істину, що в науці немає непорушних догм. Адже довгий час вважалося, що виростити кристал з шматочками іншого матеріалу усередині без дефектів неможливо. Те, що зробили співробітники лабораторії Ж.И. Алферова, можна сміливо назвати революцією в лазерній фізиці. Якщо раніше вчені, вирощуючи кристали для лазерів, вимушені були повністю управляти процесом, то тепер ситуація інша - потрібна структура росте сама. Вступ

Коли носії заряду і збудження обмежені у всіх трьох вимірах, система називається „квантовою точкою”. Це досить довільно, оскільки, наприклад, кластери, які складаються з кількох атомів необов’язково розглядаються як квантові точки. Хоча кластери менші, ніж довжина хвилі де Бройля, їх властивості критично залежать від точного числа атомів. Великі кластери мають добре визначену решітку і їх властивості вже критично не залежать від точного числа атомів. Для таких систем ми будемо використовувати термін „квантові точки” [1].

У квантовій точці рух електронів обмежений у всіх трьох вимірах і є тільки дискретні -стани у просторі. Кожний індивідуальний стан у просторі може бути представлений точкою. Тільки дискретні рівні енергій є дозволеними, вони показані дельта-піками у розподілі . Як ми можемо бачити, енергетичні зони конвертують у атомоподібні енергетичні стани з силою осцилятору, стиснутою в декілька переходів.

Ця зміна найбільш виражена на краях смуг і впливає на напівпровідники більше, ніж на метали. У напівпровідниках електронні властивості сильно пов’язані з переходами між краями валентної зони та зони провідності. На додаток до дискретності рівнів енергії необхідно також підкреслити наявність певної нульової енергії. У точці, навіть у основному стані, електрони мають енергії більші, ніж електрони у масивному твердому тілі на краю зони провідності [2].

Отже, розкриття даної теми є не лише актуальним, але й сучасним, оскільки застосування квантових точок є досить перспективним у різних галузях техніки.

У розкритті даної теми мені допомогло використання великої кількості літературних джерел.

Дана курсова робота складається з вступу, чотирьох розділів, висновків і списку використаної літератури. В першому розділі описуються квантові точки з погляду наносвіту, в другому розділі мова йде про методи отримання квантових точок, в третьому розділі – оптичні властивості квантових точок, в четвертому розділі – можливості застосування.