6.2.1 Определение потерь предварительного напряжения арматуры

Первые потери:

- от релаксации напряжений проволочной арматуры:

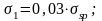
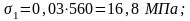
- от температурного перепада:

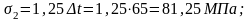
где Δt — разность между температурой нагреваемой арматуры и неподвижных упоров (вне зоны нагрева), воспринимающих усилие натяжения, ºС.

- от деформации анкеров, расположенных у натяжных устройств:

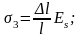
где Δl — смещение стержней в инвентарных зажимах, определяемое по формуле

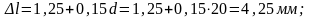
d — диаметр стержня, мм;

l — длина натягиваемого стержня, мм;

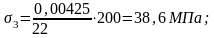
Определение усилия обжатия балки преднапряженной арматурой:

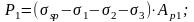
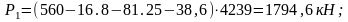
Определение эксцентриситета действия силы P₁:

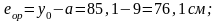
Определение расчётного изгибающего момента в середине балки от собственной массы в период ее распалубки:

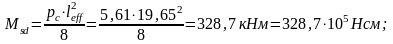
Нормативный момент:

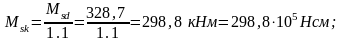
Определяем напряжения в бетоне балки на уровне центра тяжести сечения от действия собственной массы балки и усилия обжатия Р₁:

;

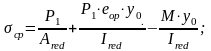
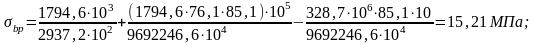
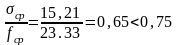- от быстронатекающей ползучести:

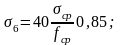
где 0,85 — коэффициент, учитывающий термообработку.

Определяем полные первые потери:

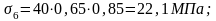
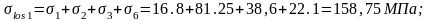
Вторые потери:

- от усадки бетона:

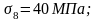
- от ползучести бетона:

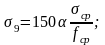
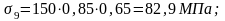
α —коэффициент, учитывающий тепловую обработку бетона, принимаемый равный 0,85.

Определение вторых потерь:

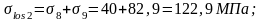
Определяем суммарные потери:

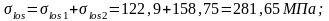
Величина обжатия балки с учетом полных потерь:

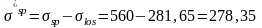
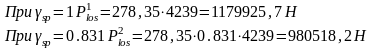
6.3 Расчет прочности балки по нормальному сечению

Определяем положение нейтральной линии из условия:

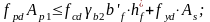
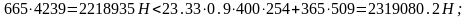
Следовательно, нейтральная ось проходит в полке.

Граничная высота сжатой зоны бетона равна:

,

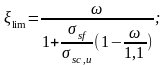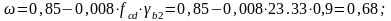
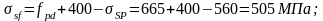
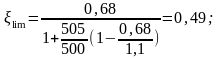
Высоту сжатой зоны находят по формуле:

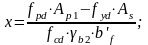
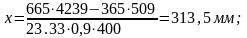
отношение х/d=31,35/151=0,21<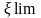 =0,49.

Изгибающий момент, воспринимаемый сечением в середине балки определяем:

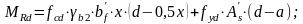
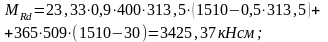
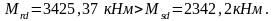
6.4 Расчет прочности сечений, наклонных к продольной оси по поперечной силе

Максимальная поперечная сила у грани опоры V_sd=432,7кН. Размеры балки у опоры: h=85см, d=85-12=73см, b=10см .

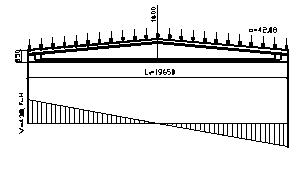
Рисунок 6.2 – К расчету балки на действие поперечных усилий

Вычисляем проекцию расчетного наклонного сечения на продольную ось. Коэффициент, учитывающий влияние свесов сжатой полки определим по формуле:

;

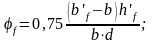
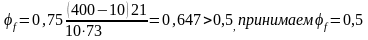влияние продольного усилия обжатия

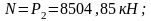
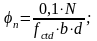
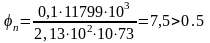принимаем φ=0,5

Параметр 1 + _f + _n 1 + 0,5 + 0,5 2> 1,5, следовательно, принимаем 1,5.

В расчетном сечении:

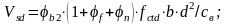
На приопорном участке принимаем хомуты 10мм из арматуры класса S400, А_sw=0,785cм². По конструктивным требованиям шаг поперечных стержней s должен быть не более 1/3h м; s=888/3=296мм, принимаем предварительно на приопорных участках s=100мм.

Усилие, воспринимаемое хомутами у опоры на единицу длины балки:

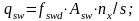
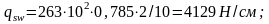
f_swd =263МПа для арматуры класса S400;

n_x=2 – число поперечных стержней в одном сечении;

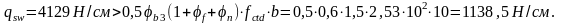
Длина проекции опасной наклонной трещины:

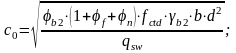
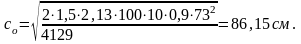
Поперечное усилие V_sw = q_swс₀ = 412986,15=353кН.< V_sd=432,7кН, следовательно, прочность сечения на действие поперечной силы не обеспечена и поэтому принимаем хомуты 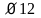мм из арматуры S500.

S=100<h/3=888/3=296мм

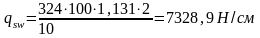
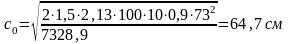
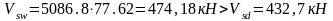,следовательно, прочность обеспечена.

Для средней половины пролета при h_о=101,7см и шаге хомутов 50см:

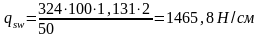
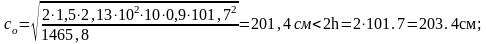
принимаем С_о= 201,4см;

Поперечное усилие

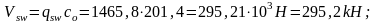
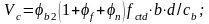
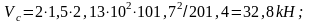
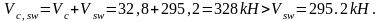
Для сечения в 1/8 пролета при h=93,35см. и шаге хомутов 15см.

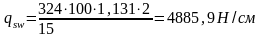
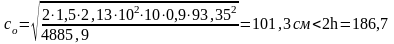принимаем с₀=101,3см.

Поперечное усилие

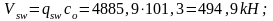
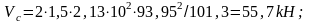
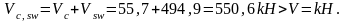
Условия выполняются во всех сечениях.