1. Статическая балансировка загрузки методом равномерной декомпозиции параллелепипеда п

В сделанных предположениях при использовании балансировки загрузки методом равномерной декомпозиции параллелепипеда П время решения задачи на процессоре можно оценить величиной

, (2.6)

время параллельного решения всей задачи - величиной

, (2.7)

а время решения задачи на одном процессоре - величиной

. (2.8)

Таким образом, схема алгоритма для аналитической оценки эффективности рассматриваемого метода балансировки загрузки имеет следующий вид:

• в квадрате строим равномерную по каждому из измерений сетку ;

• прямыми, параллельными одной из осей координат , разбиваем квадрат на одинаковых подобластей , ;

• для всех подобластей , находим количества узлов ;

• по формуле (2.6) вычисляем значение величины ;

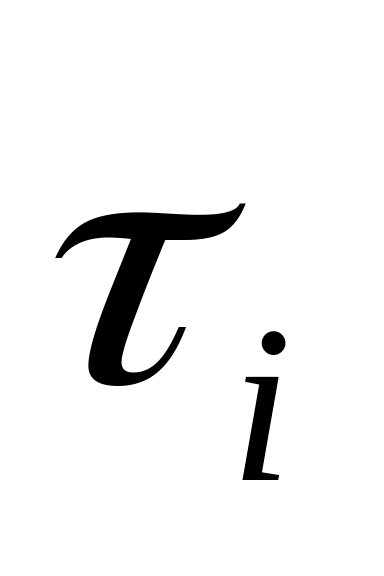• по формуле (2.7) находим величину ;

• по формуле (2.8) определяем значение величины ;

• по формуле 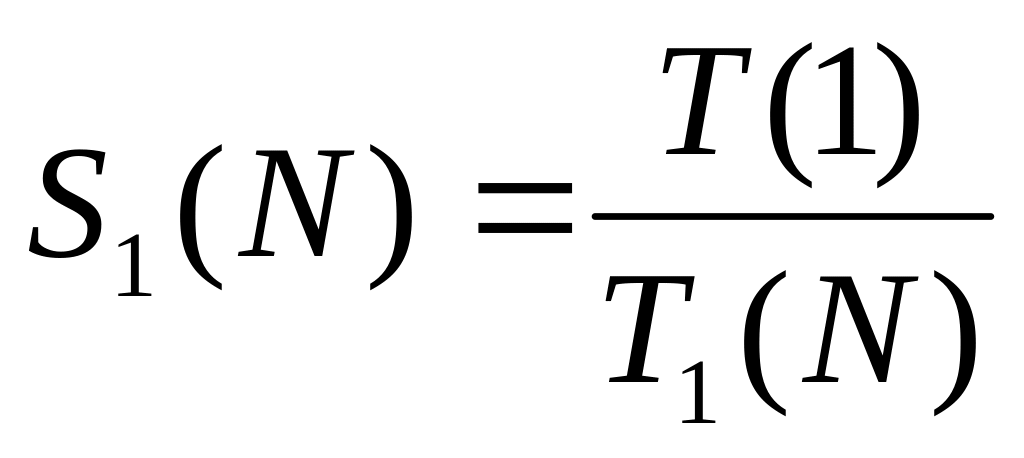находим оценку ускорения.

Поясним способ определения количеств узлов . Рассмотрим узел сетки . Положим, что квадрат разбит на подобласти , прямыми, параллельными оси , так что границы этой подобласти по оси есть точки . Тогда признаком принадлежности узла подобласти является выполнение условия (в последнем неравенстве при следует использовать знак « »). Аналогично, признаком принадлежности узла пересечению подобласти и множества является выполнение условия (в дополнение к приведенному выше условию). Таким образом, для определения количеств узлов следует последовательно рассмотреть все узлы сетки  и для каждого из них выполнить указанные выше проверки. После определения всех величин , определить величину .

Отметим, что при фиксированной величине увеличение параметра рано или поздно приведет к уменьшению площади множества и, как результат, к снижению эффективности балансировки методом равномерной декомпозиции параллелепипеда П.

Оценим асимптотическое ускорение метода при (рисунок 2.4).

Легко видеть, что в данном случае

,

откуда следует, что

.

Величина и в данном случае определяется выражением (2.8).

Таким образом, асимптотическое ускорение метода равно

. (2.9)

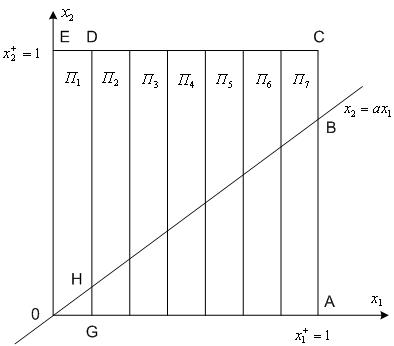
Рисунок 2.4 - К оценке асимптотического ускорения:

Положим, что количество узлов сетки кратно количеству процессоров МВС, так что , . Тогда количество узлов пропорционально части площади квадрата , принадлежащей множеству , т.е. площади трапеции . Аналогично, количество узлов пропорционально части площади прямоугольника , лежащей выше прямой , т.е. площади трапеции .

Поскольку и ,

.

Аналогично имеем , ,

.

Таким образом,

, .

Здесь учтено, что .

Окончательно, из формулы (2.9) имеем

.

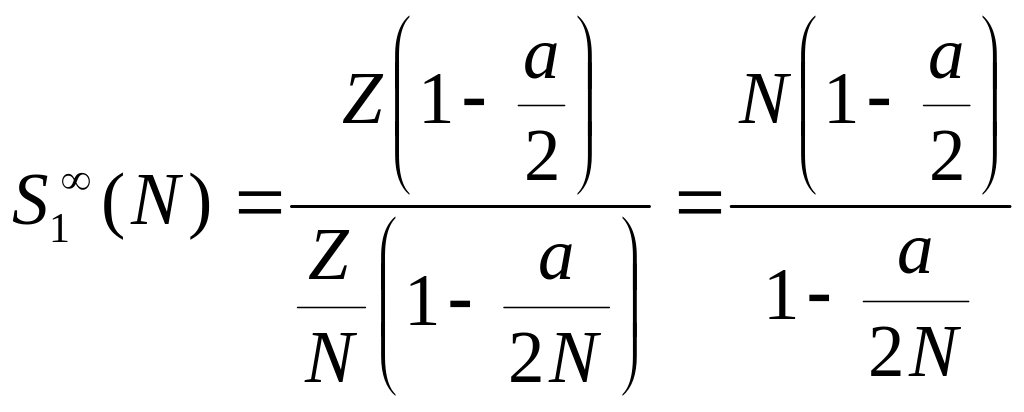2. Статическая балансировка загрузки методом равномерной декомпозиции расчетных узлов

Для данного метода балансировки загрузки время решения задачи на процессоре можно оценить величиной

, (2.10)

время параллельного решения всей задачи – величиной

, (2.11)

а время решения задачи на одном процессоре – величиной (2.8).

Таким образом, схема алгоритма для аналитической оценки эффективности балансировки загрузки методом равномерной декомпозиции расчетных узлов имеет следующий вид:

• в квадрате строим равномерную по каждому из измерений сетку ;

• находим количества узлов ;

• по формуле (2.10) вычисляем значение величины ;

• по формуле (2.11) находим величину ;

• по формуле (2.8) определяем значение величины ;

• по формуле находим оценку ускорения.

Поясним способ определения количеств узлов . Узел сетки принадлежит множеству , если выполняется неравенство . Таким образом, для определения количеств узлов следует последовательно рассмотреть все узлы сетки и для каждого из них выполнить указанную выше проверку. После этого, как указывалось выше, количество узлов определяется по формуле .

Очевидно, что и в данном случае при фиксированной величине увеличение параметра рано или поздно приведет к уменьшению площади множества . Однако на эффективность статической балансировки загрузки методом равномерной декомпозиции расчетных узлов это обстоятельство должно сказаться незначительно.