9.3.2. Загальний випадок розрахунку

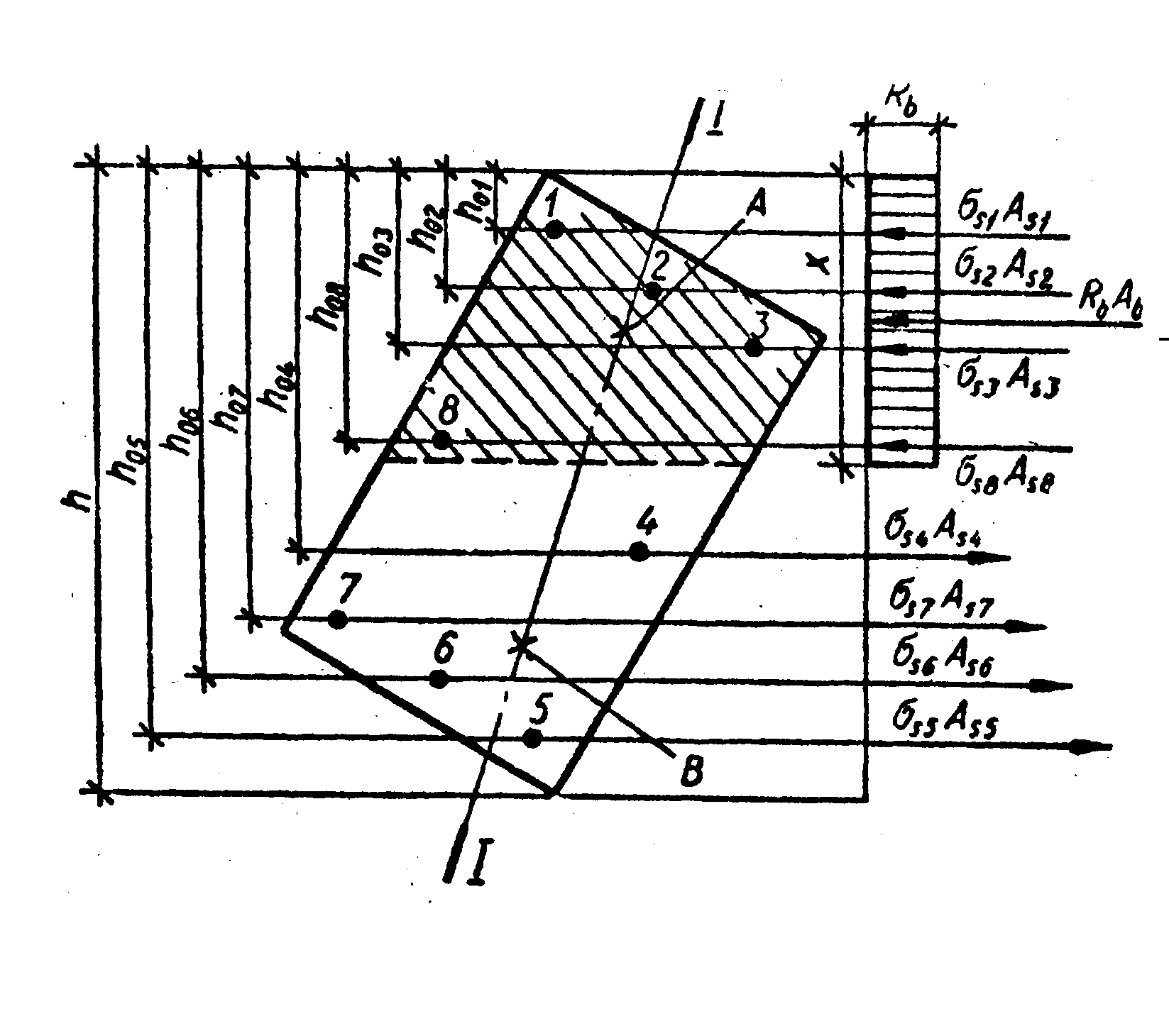
Рис. 9.3. Схема зусиль та епюра напружень у перерізі, нормальному до поздовжньої осі елемента, у загальному випадку розрахунку на міцність: І-І – площина, паралельна площині дії згинального моменту, або площина, що проходить через точки прикладання поздовжньої сили і рівнодійних внутрішніх зусиль стискання та розтягання; А – точка прикладання рівнодійних зусиль у стиснутій арматурі та бетоні стиснутої зони; В – точкаприкладання рівнодійної зусиль у розтягнутій арматурі

Умова міцності записується відносно осі ІІ-ІІ (рис. 9.3):

, (9,10)

де e – відстань від поздовжньої сили N до осі ІІ-ІІ, причому вісь ІІ-ІІ паралельна осі І-І (границя стиснутої зони); S_b – статичний момент площі стиснутої зони бетону відносно осі ІІ-ІІ; S_s – статичний момент усієї арматури відносно осі ІІ-ІІ; _si – напруження в і-тому стержні арматури.

Висоту стиснутої зони х та напруження в і-тому стержні арматури _si визначають зі спільного рішення рівнянь (9.11)...(9.14)

(9.11)

при (9.12) при ; (9.13)

при (9.14)

Для арматур класів А-І, А-ІІ, А-ІІІ та Вр-І використовують тільки рівняння (9.14), приймаючи _sp =0.

У формулах (9.11)...(9.14)  – коефіцієнт умов роботи високоміцної арматури; А_b – площа стиснутої зони бетону; А_si – площа перерізу і-того стержня арматури; – відносна висота стиснутої зони для і-того стержня; – відносні висоти стиснутої зони, що відповідають досягненню у і-тому стержні напружень R_si та R_si і визначаються за формулою для _R; обчислюючи приймають ( – коефіцієнт, що залежить від виду і способу напружування арматури); _si підставляють зі своїм знаком.

9.3.3. Елементи прямокутного поперечного перерізу при дії поздовжньої сили у площині симетрії Симетричне армування

При такому армуванні площі арматур А_s та , та рівні між собою. Умова міцності (рис. 9.4) визначається при відомій висоті стиснутої зони х

N = R_b bx – A_sp(_s6R_s – _sc) (9.15)

x = (9.16)

за формулою

х(h₀–x/2) , (9.17)

де (9.18)

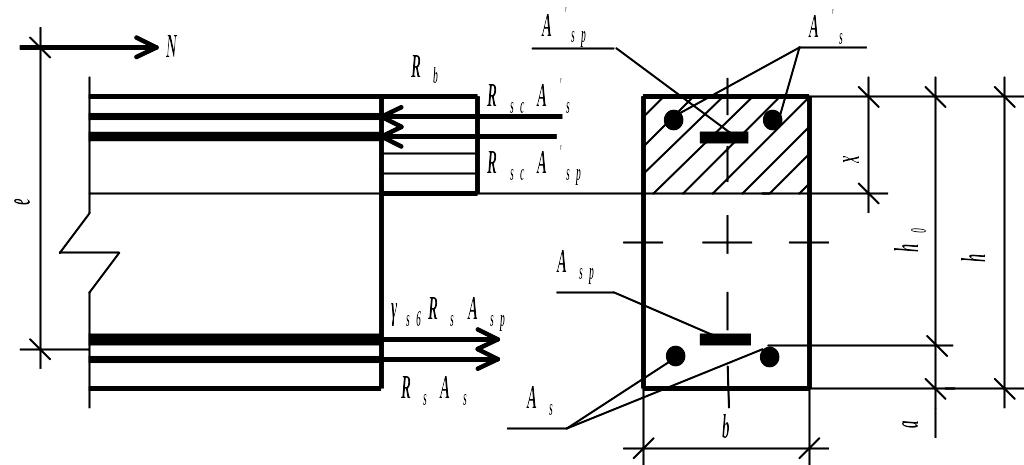
Рис. 9.4. Схема розподілу зусиль у прямокутному перерізі позацентрово стиснутого залізобетонного елемента

При цьому має виконуватися умова   _R.

Якщо елемент без попередньо напружуваної арматури, то

х = N/R_bb (9.19)

а умова міцності

Ne  R_bbx(h₀ – 0,5x) + R_sc , (9.20)

при   _R.

Якщо   _R або х > _Rh₀, то висоту стиснутої зони х визначають з рівняння

N = R_bbx + (R_s – _s)A_s, (9.21)

де (9.22)

при арматурі А-І...А-ІІІ, Вр-І і бетоні класу В30 і нижче.

Підставимо (9.22) у (9.21):

, (9.23)

де . (9.24)

При класі бетону вищому за В30

. (9.25)

Позначимо і, враховуючи (9.24), після підстановки (9.25) у (9.24) отримаємо квадратне рівняння

.

З цього рівняння визначають  і х = h₀ і перевіряють міцність перерізу за формулою (9.20).

Якщо треба підібрати площу арматури , то при х = h₀ і R_s=R_sc за (9.20) матимемо:

,

де  = а^//h₀.

Поділимо кожний член рівняння (9.21) на R_bb , позначивши

, (9.28)

. (9.29)

Потім залежно від _n (див. 9.21) визначають .

При _n  _R у (9.29) замість  підставляють _n і тоді

. (9.30)

При _n > _R

. (9.31)

У формулах (9.30) і (9.31)  визначають із (9.23) або із (9.26). Оскільки A_s невідоме, то для (9.23)

, (9.32)

а для (9.25) _s визначають за (9.32), замінивши на .

Коли ж а^/ < 0,15h₀, то площі арматур можна визначати за формулою

. (9.33)

Відмітимо, що у всіх випадках підбору площі арматури задача вирішується способом послідовних наближень (див. п. 9.2).