Зусилля попереднього обтискування бетону

Зусилля попереднього обтискування бетону приймають рівним рівнодійній зусиль в напружуваній і ненапружуваній арматурах:

,

а ексцентриситет цього зусилля відносно центра ваги зведеного перерізу визначають за умови рівності моментів рівнодійної та її складових (рис. 4.4):

(4.15)

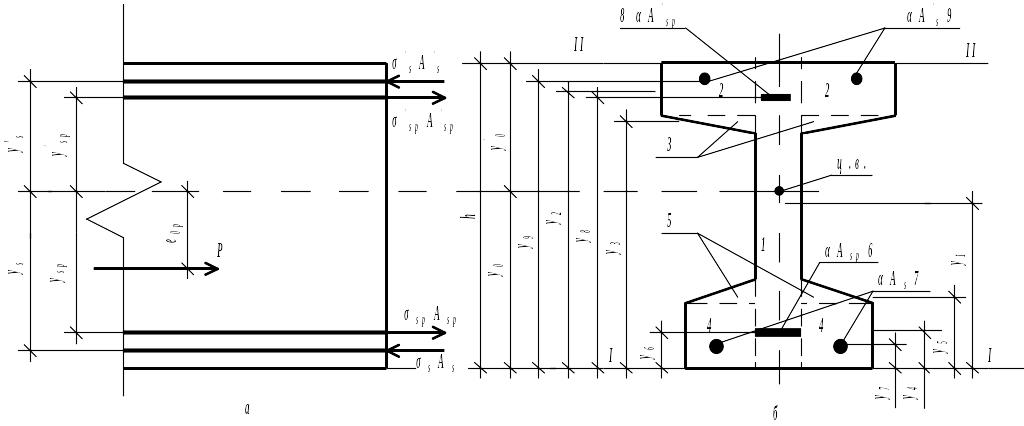
Рис. 4.4. До визначення зусилля попереднього обтискування бетону та геометричних характеристик зведеного перерізу

Зведений переріз

Зведеним називають переріз елемента, в якому площу перерізу арматури замінюють еквівалентною площею бетону. Як коефіцієнт зведення приймають відношення модулів пружності арматури та бетону

. (4.16)

Площа зведеного перерізу (див. рис. 4.4, б)

. (4.17)

Статичний момент перерізу відносно осі І-І

, (4.18)

де А_і – площа і-тої фігури перерізу; y_i – відстань від центра ваги і-тої фігури до осі І-І.

Відстань від центра ваги зведеного перерізу до осі І-І

. (4.19)

Момент інерції зведеного перерізу відносно осі, що проходить через центр ваги зведеного перерізу

, (4.20)

де І_і – момент інерції і-тої фігури відносно осі, що проходить через центр ваги фігури.

Відстань від верхньої та нижньої границі ядра перерізу до центра ваги зведеного перерізу

; . (4.21)

Напруження в бетоні при обтискуванні

Його визначають у припущенні пружної роботи перерізу та лінійної епюри напружень:

. (4.22)

Залежно від мети розрахунку напруження в бетоні визначають так.

Для встановлення контрольованого напруження в арматурі, яку натягують на бетон, напруження в бетоні визначають на рівні зусиль в напружуваній арматурі

, (4.23)

. (4.24)

При перевірці граничних напружень при обтискуванні напруження в бетоні визначають на рівні крайнього стиснутого волокна

. (4.25)

При визначенні втрат попереднього напруження від повзучості бетону _bp визначають за формулами (4.23) та (4.24).

Гранична висота стиснутої зони. Залежність напружень в арматурі від висоти стиснутої зони на стадії руйнування

В непереармованих залізобетонних елементах напруження в арматурі в стадії руйнування досягають своїх граничних значень. В розрахунках їх приймають рівними R_s (для розтягнутої арматури) і R_sc (для стиснутої арматури).

У переармованих елементах, що працюють на згинання, а також в позацентрово стиснутих при малих ексцентриситетах напруження в арматурі не досягають граничного значення, а дорівнюють величині _s. Ці напруження визначають з додаткового рівняння (крім двох рівнянь статики), що встановлює експериментальний зв’язок між напруженнями в арматурі і висотою стиснутої зони в момент руйнування.

Деформації арматури _s та відносна висота стиснутої зони =x/h₀ зв’язані між собою залежністю

, (4.26)

де _b,u– граничне вкорочування бетону при центральному стиску, яке приймають 0,002 або 0,0025; _sp–деформація арматури при її натягуванні з урахуванням втрат (для ненапружених конструкцій _sp=0); 1,1=h/h₀ – відношення висоти перерізу до його робочої висоти; =x/h₀ – відносна висота стиснутої зони при прямокутній епюрі для випадку, коли приріст деформацій в арматурі (і напружень) дорівнює нулю.

Для обчислення  використовують спрощену лінійну залежність, що враховує зв’язок деформативності та міцності бетону

, (4.27)

де  дорівнює 0,85 для важкого і 0,8 для легкого бетонів.

Величину  можна трактувати як коефіцієнт повноти фактичної епюри стискувальних напружень у бетоні або як характеристику деформативності стиснутої зони бетону. Із збільшенням міцності бетону епюра напружень змінюється від майже прямокутної до трикутної, а деформативність зменшується (рис. 4.5, а та б).

Одержане рівняння справедливе тільки в межах пружної роботи арматури.

Для елементів з ненапружуваною арматурою

(4.29)

Підставивши в рівняння (4.29) та , матимемо вираз для визначення граничної висоти стиснутої зони бетону _R, при якій напруження в арматурі досягають межі текучості сталі

(4.30)

Якщо праву та ліву частини рівняння (4.26) помножити на модуль пружності сталі E_s, то отримаємо

, (4.28)

де ; .

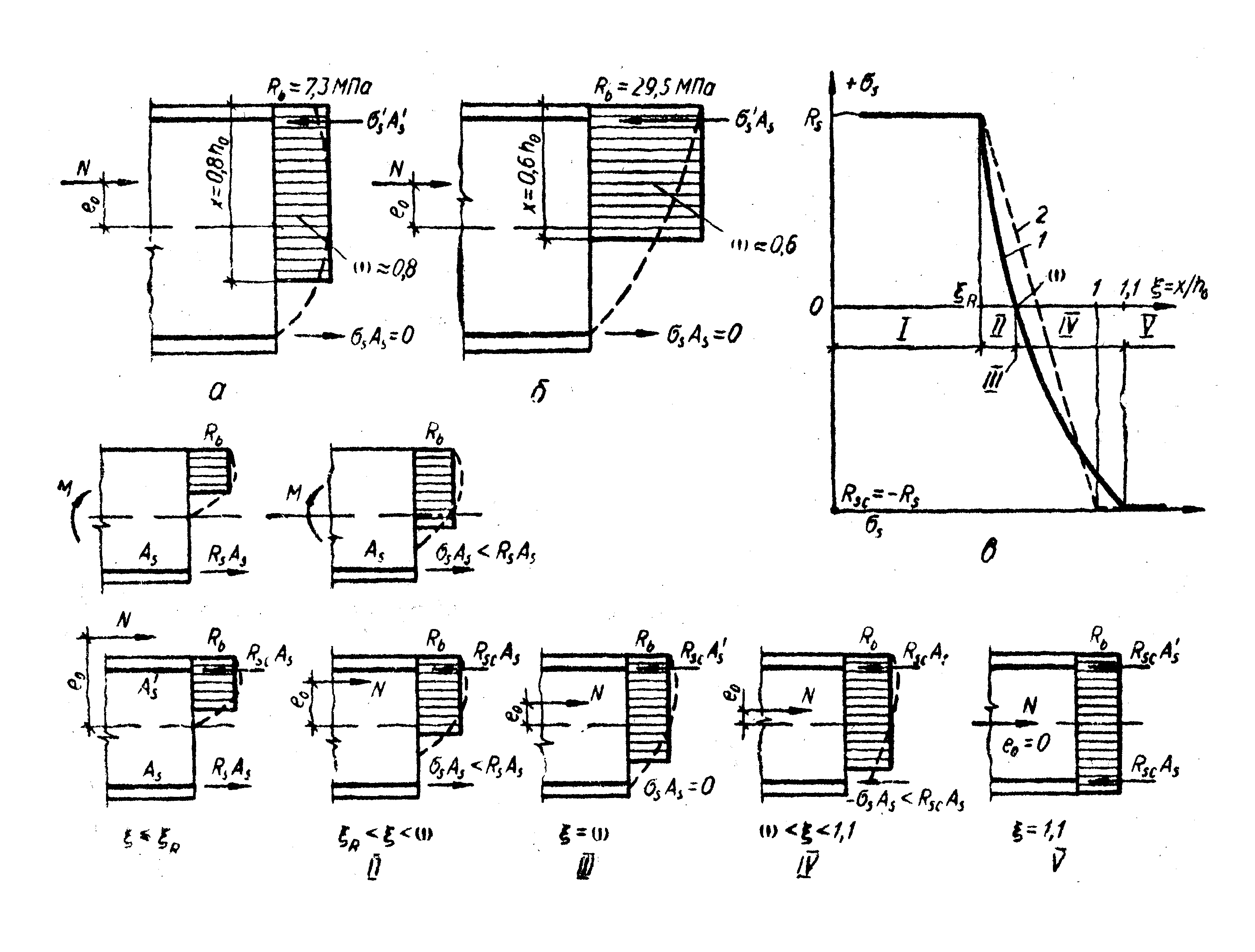
Рис. 4.5. Вплив висоти стиснутої зони бетону на напруження в арматурі: а  залежність між коефіцієнтом  та класом бетону В12,5; б  те саме, при В60; в  залежність між напруженнями в арматурі _s та відносною висотою стиснутої зони бетону на стадії руйнування елемента; г  напружений стан у перерізах елементів, що працюють на згинання та в позацентрово стиснутих на стадії руйнування; I…V  випадки напруженого стану перерізу; 1  залежність за формулою (4.29); 2  залежність за формулою (4.31)

Для елементів, виготовлених із бетонів класів В30 і нижче, армованих ненапружуваною арматурою класів Вр-І, А-І, А-ІІ і А-ІІІ, рекомендується використовувати спрощену лінійну залежність для напружень в інтервалі напружень від R_s до

(4.31)

На рис. 4.5,в наведено графіки залежності , побудовані за формулами (4.29) і (4.31). Штриховими лініями показано фактичні епюри напружень у бетоні стиснутої зони, суцільними – розрахункові при можливих випадках напруженого стану в стадії руйнування.

Випадок І.Характеризується відносною висотою _R і напруженнями в арматурі A_s, що дорівнюють _s=R_s. Такий напружений стан виникає в момент руйнування елементів, що згинаються, із звичайним або максимальним відсотком армування і в позацентрово стиснутих елементах у випадку великих ексцентриситетів (рис. 4.5, г, 1), що відповідає ділянці 1 на графіку (рис. 4.5, в).

Випадок 2. Відносна висота стиснутої зони бетону лежить в межах _R. Цей напружений стан характерний для переармованих елементів, що працюють на згинання, і позацентрово стиснутих при малих ексцентриситетах. Відповідає ділянці 2 на графіку (рис. 4.5, в). У розтягнутій арматурі A_s напруження _sR_s (рис. 4.5, г, ІІ).

Випадок 3. Відносна висота стиснутої зони бетону =. Фактична епюра напружень в бетоні проходить через арматуру A_s, а напруження _s дорівнюють нулю (точка ІІІ на графіку рис. 4.5, в). Розрахункова епюра прямокутна вкорочена, а тому <1 (рис. 4.5, г, ІІІ).

Випадок 4. Відносна висота стиснутої зони лежить у межах  1,1, що характерно для позацентрово стиснутих елементів при малих ексцентриситетах, і відповідає ділянці IV на графіку (рис. 4.5, в). Фактична епюра напружень в бетоні криволінійна, близька до трапецуватої, тому напруження в арматурі A_s стискувальне, але _s < R_sc (рис. 4.5, г, IV).

Випадок 5. Весь переріз рівномірно стиснутий,  = 1,1. Напруження в арматурі A_s досягають межі текучості при стисканні (точка V на графіку рис. 4.5, в). Напружений стан характерний для центрально стиснутих елементів, а фактична і розрахункова епюра напружень в бетоні збігаються (рис. 4.5, г, V).

Формули (4.28) і (4.29) справедливі лише для арматури класу Вр-І, А-І…А-ІІІ, які мають явно виражену площинку текучості. Для високоміцної арматуриА-IV…A-VII, В-ІІ і Вр-ІІ, що не має площинки текучості, ці формули використати не можна.

Універсальна формула для обчислення граничної висоти стиснутої зони при будь-якому армуванні має вигляд:

, (4.32)

де _sR – умовні напруження в розтягнутій арматурі:

; (4.33)

_sc,u – граничні напруження в арматурі стиснутої зони, які становлять 400 МПа при _в2=1 і 500 МПа при _в2=0,9.

При розрахунках на міцність розрахункові напруження високоміцної арматури мають помножуватися на коефіцієнт умов роботи

, (4.34)

де  – граничне значення коефіцієнта _s6, яке залежно від класу сталі приймають рівним: для A-IV – 1,2, для A-V, В-ІІ, Вр-ІІ, К-7 і К-19 – 1,15, для A-VI...A-VIII – 1,1.