ЛР.05 – Реалізація алгоритмів сортування масивів (обмінами, вибором)

Мета роботи: реалізувати алгоритми сортування масивів.

Зміст роботи: розробити блок-схему алгоритму та за допомогою пакету MS Visual Studio створити консольну програму, яка здійснює сортування елементів масиву за різними алгоритмами (обмінами, вибором). Правильність виконання завдання перевірити на тестових даних. Хід виконання та результати внести до звіту.

Структура звіту: Титульний аркуш (тема, назва лабораторної, П.І.Б. студента, П.І.Б. керівника), далі для кожного завдання: текст завдання, текстовий опис алгоритму виконання завдання, блок-схема алгоритму відповідно до ГОСТ 19.701-90, програмний код зі збереженням форматування, копії екрану виконання програми.

1. Теоретичні відомості

1. Сортування обмінами

Основна дія сортування обмінами - порівняння двох елементів і, якщо результат порівняння негативний, перестановка їх місцями:

Якщо при i < j має місце відношення a[i] > a[j], то необхідно переставити a[i] і a[j]. У найбільш простому варіанті порівнюються елементи, що розташовані поруч, тобто елементи a[j] і a[j+1].

Розв'язування.

Алгоритм сортування обмінами здійснює n-1 лінійний перегляд масиву А. У результаті кожного перегляду найбільший елемент переглянутої частини масиву «спливає» на останнє місце в результаті порівняння і перестановки, якщо потрібно, двох сусідніх елементів. Перший перегляд здійснюється у всьому масиві, а кожен наступний перегляд – у діапазоні, на одиницю меншому. Таким чином, права частина масиву поступово стає упорядкованою.

На рисунку 5.1. ці елементи – від a[k] до a[n] - заштриховані сірим кольором. На кожнім кроці перегляду порівнюються два елемента, що стоять поруч. На рисунку – це елементи a[i] і a[i+1]. Якщо вони розташовані неправильно (має місце відношення a[i] > a[i+1]), алгоритм переставляє їх місцями.

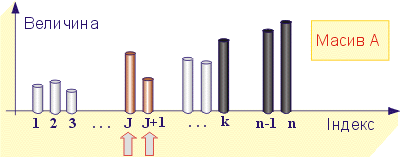
Рис 5.1. Алгоритм сортування обмінами.

Текст програми мовою Паскаль:

Program BublSort;

Const

n = 20;

Var

a : array[1..n] of Data;

I, j : Integer;

b : Data;

Begin

For i := n - 1 downto 1 do

For j := 1 to i do

If a[j] > a[j+1]

then begin

b := a[j+1];

a[j+1] := a[j];

a[j] := b

end;

End.

Аналіз алгоритму сортування обмінами.

Аналіз алгоритму полягає в обґрунтуванні його властивостей. Найважливішими властивостями алгоритму є: коректність (правильність одержання результату), оцінка складності за часом, обсяг пам'яті, що використовується, і інші властивості.

Для обґрунтування коректності алгоритму сортування необхідно показати, що алгоритм завжди (незалежно від вхідних даних) завершує свою роботу і його результат - упорядкований по зростанню масив.

Оцінка складності алгоритму за часом полягає в підрахуванні кількості порівнянь C(n) і кількості перестановок M(n) алгоритму в гіршому випадку (якщо приходиться переставляти кожну порівнювану пару елементів масиву) і в середньому випадку.

Даний алгоритм для сортування вихідного масиву не використовує додаткові масиви, тобто алгоритм сортує масив “на місці”. Тому його складність по пам'яті – константа (залежить від кількості елементів у масиві).

До інших властивостей алгоритму можна віднести властивість стійкості. Алгоритм сортування називається стійким, якщо він не переставляє місцями рівні елементи.

Здійснимо аналіз алгоритму сортування обмінами.

Завершеність і Коректність

Алгоритм BublSort завжди завершує свою роботу, оскільки він використовує лише цикли з параметром (for to do; for downto do), і в тілі циклів параметри ( змінні i та j ) примусово не змінюються.

Внутрішній цикл алгоритму (з параметром j) здійснює послідовний перегляд перших i елементів масиву. На кожному кроці перегляду порівнюються і, якщо це необхідно, переставляються два сусідніх елементи. Таким чином, найбільший серед перших i+1 елементів “спливає” на i+1-е місце. Тому після виконання оператора If має місце співвідношення:

a[j+1] = Max (a[1], ..., a[i], a[j+1])

а після завершення циклу (i = j) має місце співвідношення

a[i+1] = Max(a[1], ..., a[i], a[i+1])

Зовнішній цикл (з параметром i) керує довжиною частини масиву, що переглядається. Після кожного виконання тіла циклу довжина частини масиву для перегляду зменшується на 1. Тому після завершення внутрішнього циклу має місце співвідношення: a[i+1] ≤ a[i+2] ≤ ... ≤ a[n].

Після завершення зовнішнього циклу одержимо: а[1] ≤ a[2], a[2] ≤ a[3] ≤ ... ≤ a[n] тобто масив відсортований.

Ефективність за часом

Зовнішній цикл алгоритму виконується n-1 раз. Внутрішній цикл виконується і раз, де і приймає значення: і = n-1, n-2, ..., 1. Кожне виконання тіла внутрішнього циклу полягає в одному порівнянні і, можливо, в одній перестановці. Тому кількість порівнянь визначається формулою

C(n) = 1+2+ ... +n-1 = n*(n-1)/2,

А кількість перестановок - M(n)≤n*(n-1)/2

У гіршому випадку, коли елементи вихідного масиву розташовані в порядку спадання, ці формули приймають вид: C(n) ~ n², M(n) ~ n²