2.4. Площадь поверхности вращения
Пусть
непрерывно дифференцируемая на отрезке
функция. Площадь
поверхности, образованной при вращении
графика этой функции вокруг оси
равна
(18)
Пусть кривая задана
уравнениями
,
где
;
и
– непрерывно дифференцируемые на
функции. Площадь
поверхности, образованной при вращении
данной кривой вокруг оси
,
равна
.
(19)
При аналогичных условиях площадь поверхности, образованной при вращении кривой вокруг оси , соответственно равна
,
(20)
.
(21)
Площадь поверхности,
образованной при вращении вокруг
полярной оси кривой
,
равна
,
(22)
где
– непрерывно дифференцируемая на
функция. При этом же условии площадь
поверхности, образованной при вращении
вокруг луча
кривой
,
,
равна
.
Пример
41. Вычислить
площадь поверхности, образованной
вращением вокруг оси
кривой
,
.
Решение.
.
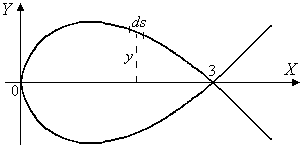
Пример 42. Найти
площадь поверхности, образованной
вращением вокруг оси
петли кривой
(рис. 21).
Рис. 21 |
Рис. 22 |
Решение. Для
верхней части кривой при
имеем:
.
Отсюда
.
На основании формулы (18) площадь
поверхности
.
Пример 43.
Найти площадь поверхности, образованной
вращением вокруг оси
дуги кривой
от
до
.
Решение. Площадь поверхности равна несобственному интегралу
.
Сделав подстановку
,
,
получим
,
при
при
,
отсюда
.
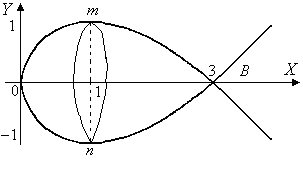
Пример
44. Вычислить
площадь поверхности, образованной
вращением вокруг оси
дуги кривой, заданной параметрически:
,
заключенной между точками пересечения
ее с осью
.
Решение.
Полагая
,
находим
и
откуда
и
.
Следовательно, кривая пересекает ось
в двух точках
и
.
При изменении знака параметра
функция
знака не меняет, а функция
меняет знак. Это означает, что кривая
симметрична относительно оси
(рис. 22).
Для нахождения
площади поверхности достаточно
ограничиться нижней частью кривой
,
соответствующей изменению параметра
от
до
.
,
,
.
Следовательно,
.
Пример
45. Вычислить
площадь поверхности, образованной
вращением циклоиды
(рис. 23).
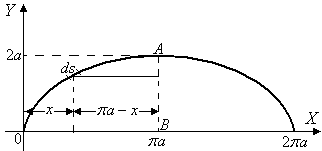
Рис. 23
1) вокруг оси ; 2) вокруг ее оси симметрии.
Решение. При вращении вокруг оси площадь поверхности находим по формуле (20)
.
Во втором случае
искомая поверхность образуется вращением
дуги циклоиды вокруг прямой
.
Принимая
за независимую переменную и учитывая,
что ось вращения сдвинута относительно
координатной оси
на расстояние
,
будем иметь:
.
Переходя к переменной , получим:
.
Пример 46. Вычислить площадь поверхности, образованной вращением лемнискаты
1) вокруг полярной оси; 2) вокруг прямой .
Решение.
Действительные значения для
получаются при
,
т.е. при
(правая ветвь лемнискаты) и при
(левая ветвь лемнискаты) (см. рис. 12).
При вращении вокруг полярной оси левая и правая ветви лемнискаты описывают одинаковые поверхности, поэтому будем считать удвоенную площадь поверхности, описываемой правой ветвью.
Надо иметь в виду,
что верхняя часть дуги при
и нижняя часть при
описывают одну и ту же поверхность,
поэтому площадь искомой поверхности
,
.
.
2) Площадь поверхности,
образованной вращением дуги
вокруг луча
вычисляется по формуле 
.
(23)
Поэтому
.