
- •Глава 1 определенный интеграл
- •1.1. Определенный интеграл как предел суммы
- •1.2. Вычисление определенных интегралов с помощью неопределенных
- •1.3. Несобственные интегралы
- •Глава 2 геометрические приложения
- •2.1. Площади плоских фигур
- •2.2. Длина дуги кривой
- •2.3. Объем тела вращения
- •2.4. Площадь поверхности вращения
- •Глава 3 задачи и ответы
- •3.1. Задачи
- •3.2. Ответы
2.2. Длина дуги кривой
![]() .
Длина дуги в прямоугольных координатах.
.
Длина дуги в прямоугольных координатах.
Длина
![]() дуги гладкой кривой
,
содержащейся между двумя точками с
абсциссами
и
дуги гладкой кривой
,
содержащейся между двумя точками с
абсциссами
и
![]() ,
равна
,
равна
 .
(9)
.
(9)
Пример 24. Найти
длину дуги полукубической параболы
![]() ,
заключенной между началом координат и
точкой
,
заключенной между началом координат и
точкой
![]() (рис. 14)
(рис. 14)
Решение.
Функция
![]() определена при
определена при
![]() ,
и так как точка
,
и так как точка
![]() лежит в первой четверти, то
лежит в первой четверти, то
![]() ,
следовательно,
,
следовательно,
![]() ,
,

 .
.
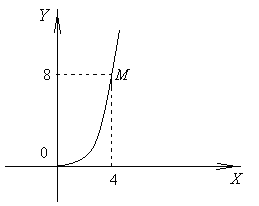
Рис. 14
 .
.
Пример 25. Найти
длину дуги кривой
 ,
заключенной между точками с ординатами
,
заключенной между точками с ординатами
![]() и
и
![]() .
.
Решение.
В этой задаче за независимую переменную
удобнее принять
![]() ,
тогда
,
тогда

и
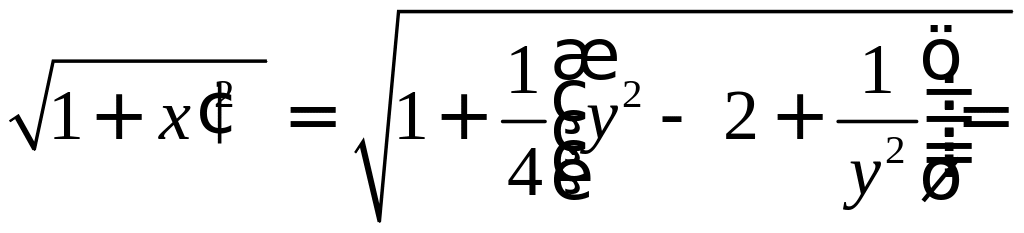
 .
.
Следовательно,

 .
.
. Длина дуги кривой, заданной параметрически.
Если кривая,
лежащая на плоскости, задана уравнениями
в параметрической форме
,
![]() ,
,
![]() ,
где
,
где
![]() – непрерывно дифференцируемые функции,
то длина
дуги кривой равна
– непрерывно дифференцируемые функции,
то длина
дуги кривой равна
 .
(10)
.
(10)
Если кривая в
пространстве задана параметрическими
уравнениями
,
,
![]() ,
где
и
,
где
и
![]() – непрерывно дифференцируемые функции,
то длина
кривой вычисляется по формуле
– непрерывно дифференцируемые функции,
то длина
кривой вычисляется по формуле
 .
.
Пример 26. Найти длину одной арки циклоиды (рис. 15)
![]() .
.
Решение.
Имеем
![]() и
и
![]() .
.
Поэтому

Пределы интегрирования
![]() и
и
![]() соответствуют крайним точкам арки
циклоиды.
соответствуют крайним точкам арки
циклоиды.
Рис. 15 |
Рис. 16
|
Пример
27. Найти
длину астроиды
![]() (рис. 16)
(рис. 16)
Решение.
Вычислить длину астроиды проще, если
задать ее в параметрическом виде:
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]() .
.
Так как кривая симметрична относительно обеих осей, то достаточно найти ее длину в первой четверти
 .
.
Пример 28. Найти длину дуги кривой
 .
.
Решение.
Так как
![]() ,
,
![]() ,
то
,
то
 .
.
Пример 29. Найти длину дуги кривой
![]() .
.
Решение.
Имеем
![]() ,
,
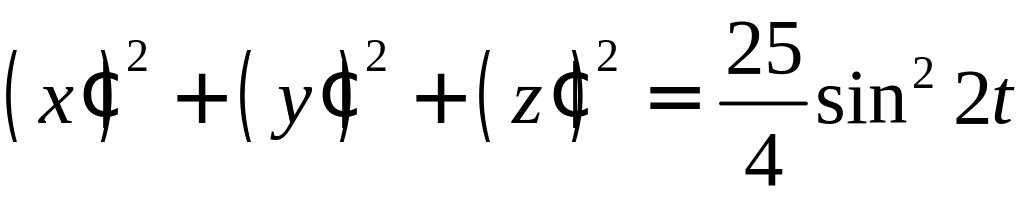 .
Тогда
.
Тогда
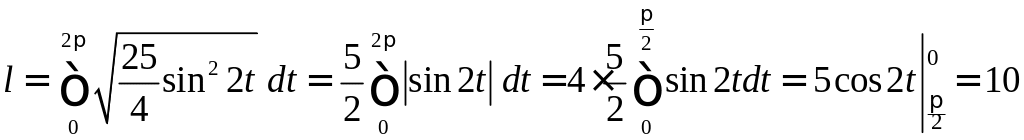 .
.
. Длина дуги кривой, заданной в полярных координатах.
Если гладкая
кривая задана уравнением
в полярных координатах
![]() и
,
то длина дуги
равна
и
,
то длина дуги
равна
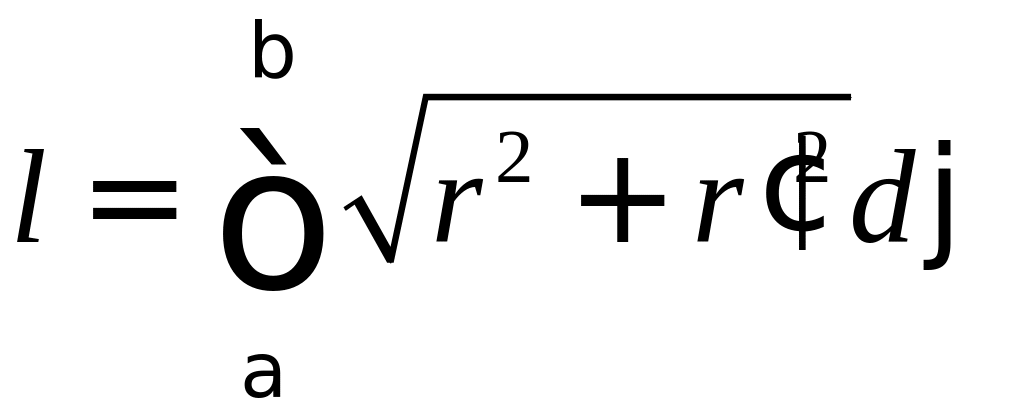 ,
(11)
,
(11)
где
![]() и
и
![]() – значение полярного угла в крайних
точках дуги
– значение полярного угла в крайних
точках дуги
![]() .
.
Если гладкая
кривая задана уравнением
![]() в полярных координатах
и
в полярных координатах
и
![]() ,
то длина дуги
находится по формуле
,
то длина дуги
находится по формуле
 ,
(12)
,
(12)
где
![]() и
и
![]() – значения полярного радиуса в крайних
точках дуги
– значения полярного радиуса в крайних
точках дуги
![]() .
.
Пример 30.
Найти длину всей кривой
Решение.
Имеем
|
|
 .
.
Пример 31.
Найти длину дуги кривой
 .
.
Решение.
 .
.
Следовательно,
 .
.
Пример 32.
Найти длину дуги
![]() .
.
Решение. Аналогично предыдущему примеру, получим

 .
.
2.3. Объем тела вращения
. Объем тела вращения в прямоугольных координатах.
Объемы
тел, образованных вращением криволинейной
трапеции, ограниченной кривой
,
осью
и двумя вертикалями
и
,
вокруг осей
и
![]() выражаются соответственно формулами:
выражаются соответственно формулами:
 (13)
(13)
 (14)
(14)
Пример 33.
Вычислить объемы тел, образованных
вращением фигуры:
![]() и
и
![]()
а) вокруг оси ;
б) вокруг оси
Решение.
а)

б)
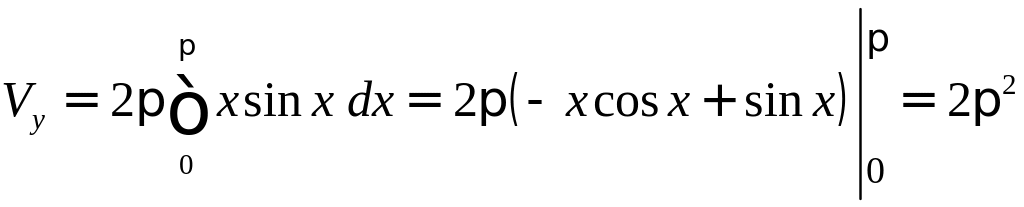 .
.
Объем тела,
образованного вращением около оси
фигуры, ограниченной кривой
![]() ,
осью
и двумя параллелями
,
осью
и двумя параллелями
![]() и
и
![]()
![]() ,
можно определить по формуле:
,
можно определить по формуле:
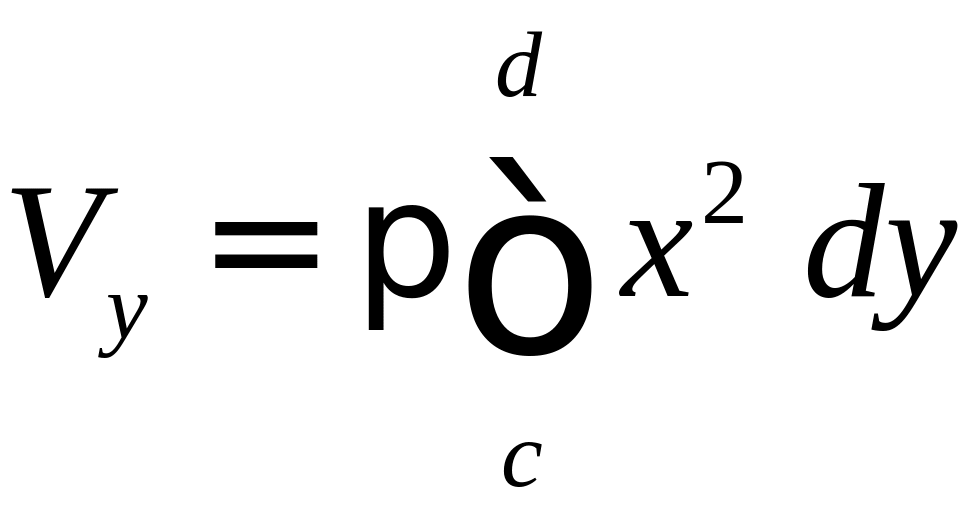 ,
(15)
,
(15)
получающейся из
приведенной выше формулы (13) путем
перестановки координат
![]() и
.
и
.
Пример
34. Вычислить
объем тела, полученного вращением вокруг
оси
фигуры, ограниченной линиями
![]() .
.
Решение. По формуле (15) имеем

 .
.
В более общем
случае объемы тел, образованных вращением
фигуры, ограниченной кривыми
![]() и
и
![]() (причем
(причем
![]() )
и прямыми
и
,
вокруг координатных осей
и
вычисляем
как разность двух объемов.
)
и прямыми
и
,
вокруг координатных осей
и
вычисляем
как разность двух объемов.
Пример
35. Вычислить
объем тела, полученного вращением вокруг
оси
фигуры, ограниченной параболами
![]() и
и
![]() .
.
Решение.
Очевидно, что
 на отрезке от начала координат до точки
пересечения парабол (рис. 18). Найдем
ординаты точек пересечения парабол,
исключив
из системы уравнений:
на отрезке от начала координат до точки
пересечения парабол (рис. 18). Найдем
ординаты точек пересечения парабол,
исключив
из системы уравнений:
 .
.
Получим
![]() .
Следовательно,
.
Следовательно,
 .
.

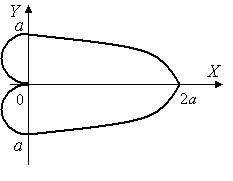
Рис. 18 Рис. 19
Пример
36. Найти
объем фигуры, образованной вращением
кривой
 (локон Аньези) вокруг оси
.
(локон Аньези) вокруг оси
.
Решение. Функция непрерывная на всей числовой оси и четная (рис. 6). Поэтому
![]()

 .
.
Второй интеграл возьмем по частям
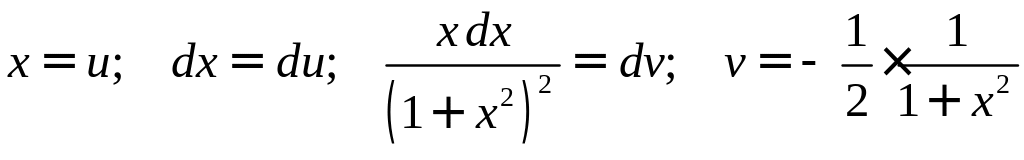 .
.
В результате получим
 .
.
![]() .
Объемы тел вращения, заданных
параметрически.
.
Объемы тел вращения, заданных
параметрически.
Если кривая задана
параметрически:
![]() ,
то объемы тел вращения вычисляются по
формулам, аналогичным формулам (13) и
(14):
,
то объемы тел вращения вычисляются по
формулам, аналогичным формулам (13) и
(14):
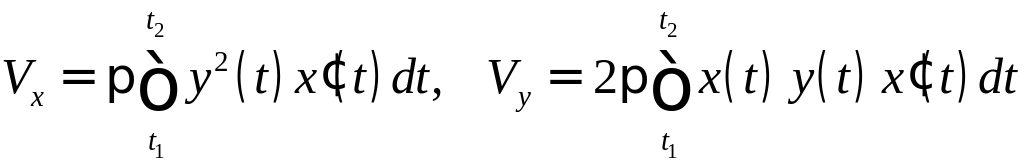 .
.
Пример 37. Найти объем тела, образованного вращением
фигуры:
![]() (см. рис. 15)
(см. рис. 15)
а) вокруг оси
![]() ,
б) вокруг оси
,
б) вокруг оси
![]() ,
в) вокруг прямой
,
в) вокруг прямой
![]() .
.
Решение.
, тогда
а)

 ,
,
так как
 равны нулю.
равны нулю.
б)


 ,
так как
,
так как

в) Перейдем к новой системе координат по формулам
![]() (рис. 20).
(рис. 20).

Рис. 20
Для нахождения
объема
![]() «воронки» ОАВСМ
применим формулу (13) в новой системе
координат.
«воронки» ОАВСМ
применим формулу (13) в новой системе
координат.
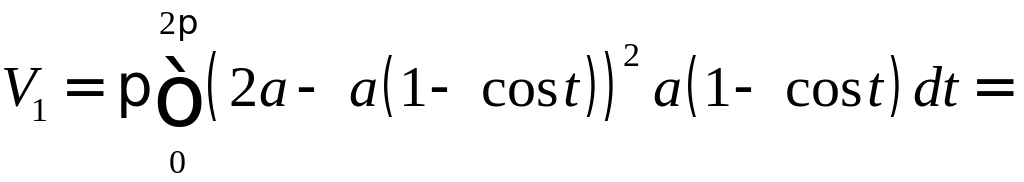

![]() .
.
Для нахождения
искомого объема надо от объема цилиндра
ОАВС
вычесть объем
![]() «воронки»
«воронки»
![]() .
.
Следовательно,
искомый объем
![]() равен
равен
![]() .
.
![]() .
Объем тела
вращения, заданного в полярных координатах.
.
Объем тела
вращения, заданного в полярных координатах.
Объем тела,
образованного вращением вокруг полярной
оси фигуры
![]() ,
где
,
где
![]() (
и
– полярные координаты), равен
(
и
– полярные координаты), равен
 .
(16)
.
(16)
Пример
38. Найти
объем тела, образованного вращением
кардиоиды
![]() вокруг полярной оси.
вокруг полярной оси.
Решение. Воспользуемся формулой (16). Полярная ось делит кардиоиду на две равные части (рис. 19), которые заметают один и тот же объем. Поэтому интегрируем от 0 до и получаем
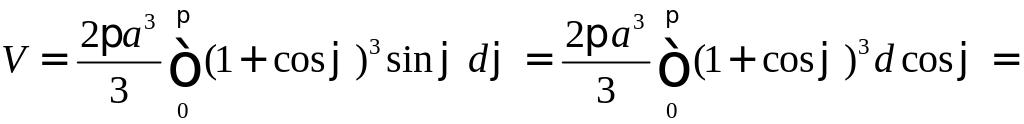
 .
.
Пример 39. Найти объем тела, образованного вращением
фигуры, ограниченной
линиями
![]() вокруг полярной оси.
вокруг полярной оси.
Решение.
При
![]() ,
поэтому, применяя формулу (16),
,
поэтому, применяя формулу (16),
получим
 .
.
(Последний интеграл берется по частям).
Объем тела,
образованного вращением вокруг луча
![]() фигуры
фигуры
![]() ,
вычисляется по формуле
,
вычисляется по формуле
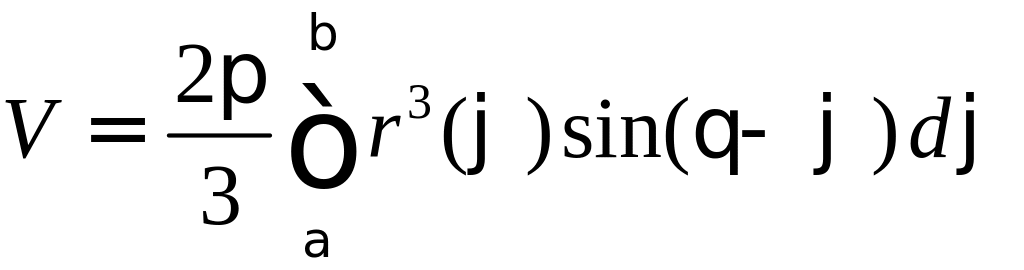 .
(17)
.
(17)
Пример
40. Найти
объем тела, образованного вращением
лемнискаты Бернулли
![]() (см. рис. 12)
(см. рис. 12)
вокруг оси ; 2) вокруг прямой
 .
.
В первом случае
угол
![]() и
и
![]() ,
поэтому объем
,
поэтому объем
тела вращения будем искать по формуле
 .
.
Так как лемниската симметрична относительно оси , то имеем
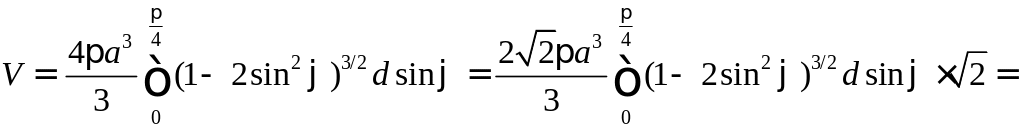
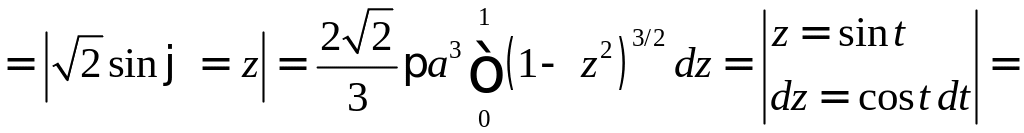
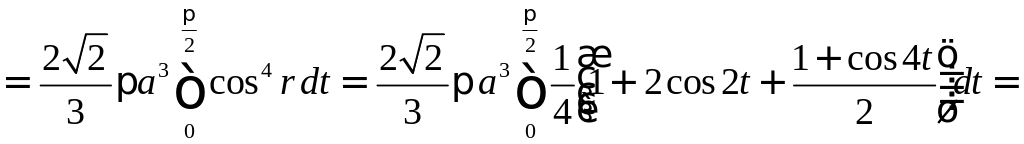
 .
.
Во втором случае
луч, вокруг которого происходит вращение,
идет под углом
![]() ,
поэтому
,
поэтому
![]() ,
и две ветви лемнискаты при вращении
создают одинаковые объемы, поэтому
,
и две ветви лемнискаты при вращении
создают одинаковые объемы, поэтому
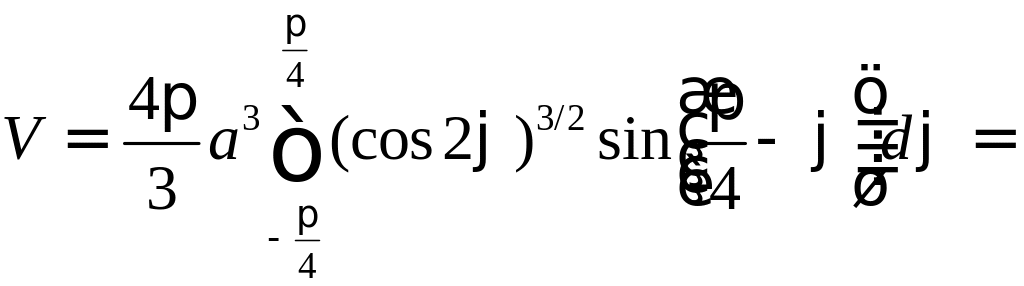

 .
.
Второй интеграл равен нулю, так как область интегрирования симметрична относительно , а подынтегральная функция нечетная, в первом интеграле подынтегральная функция четная, поэтому
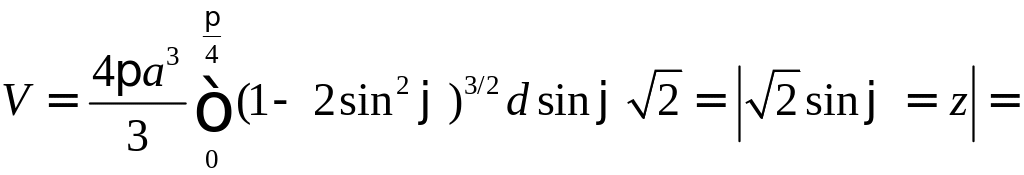
 .
.

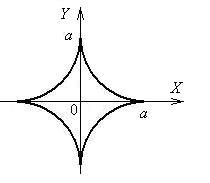
 (рис. 17). Вся кривая описывается точкой
(рис. 17). Вся кривая описывается точкой
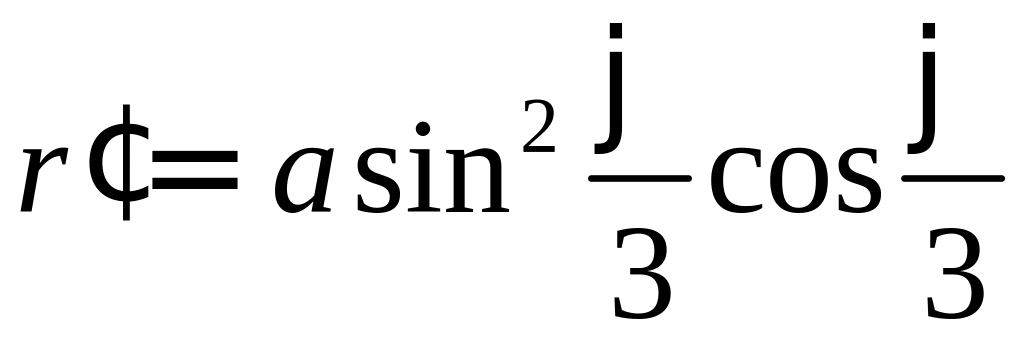 ,
поэтому длина всей кривой
,
поэтому длина всей кривой
 Рис.
17
Рис.
17