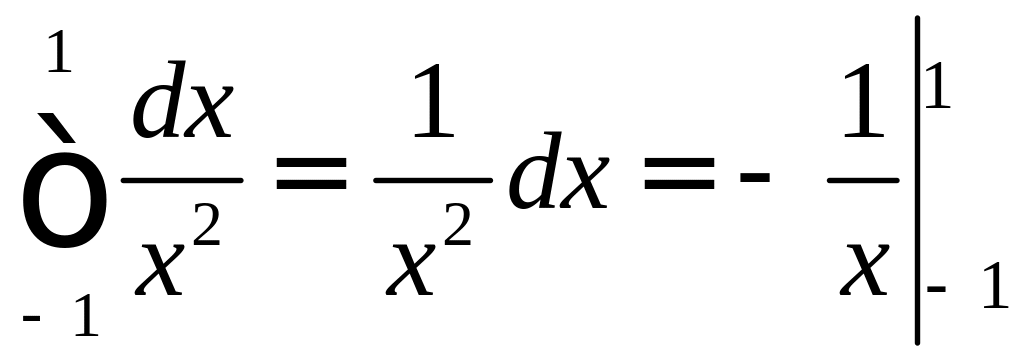Глава 1 определенный интеграл

1.1. Определенный интеграл как предел суммы

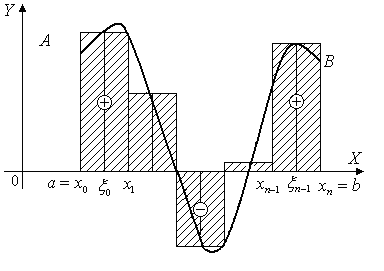
. Интегральная сумма. Пусть функция определена и непрерывна на отрезке , где – произвольное разбиение этого отрезка на частей (рис. 1). Сумма вида

, (1)

где

называется интегральной суммой функции на . Геометрически представляет собой алгебраическую сумму площадей соответствующих прямоугольников (рис. 1).

. Определенный интеграл. Предел суммы при условии,

что число разбиений стремится к бесконечности, а наибольшая из разностей – к нулю, называется определенным интегралом функции в пределах от до , т.е.

Рис. 1

. (2)

Если функция непрерывна на , то она интегрируема на , т.е. предел (2) существует и не зависит от способа разбиения промежутка интегрирования на частичные отрезки и от выбора точек на этих отрезках. Геометрически определенный интеграл (2) представляет собой алгебраическую сумму площадей фигур, составляющих криволинейную трапецию , в которой площади частей, расположенных выше оси , берутся со знаком плюс, а площади частей, расположенных ниже оси , – со знаком минус (рис. 1).

По определению .

1.2. Вычисление определенных интегралов с помощью неопределенных

. Определенный интеграл с переменным верхним пределом. Если функция непрерывна на отрезке , то функция

есть первообразная для функции , т.е.

при .

. Формула Ньютона-Лейбница. Если , то

.

Первообразная вычисляется путем нахождения неопределенного интеграла

.

Пример 1. Найти интеграл .

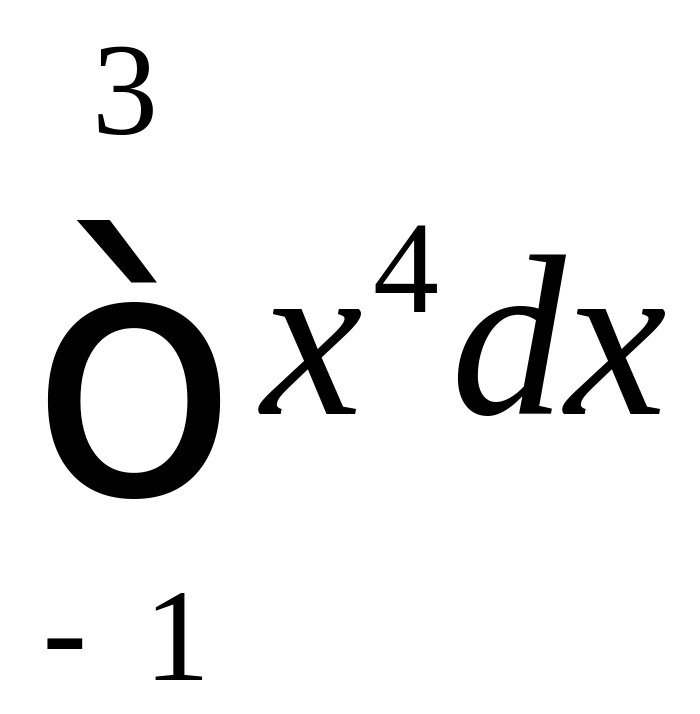Решение. .

. Замена переменной в определенном интеграле.

Если функция непрерывна на отрезке и – функция, непрерывная вместе со своей производной на отрезке где и , причем определена и непрерывна на отрезке , то

.

Пример 2. Найти

.

Решение. Положим

Тогда и, следовательно, можно принять

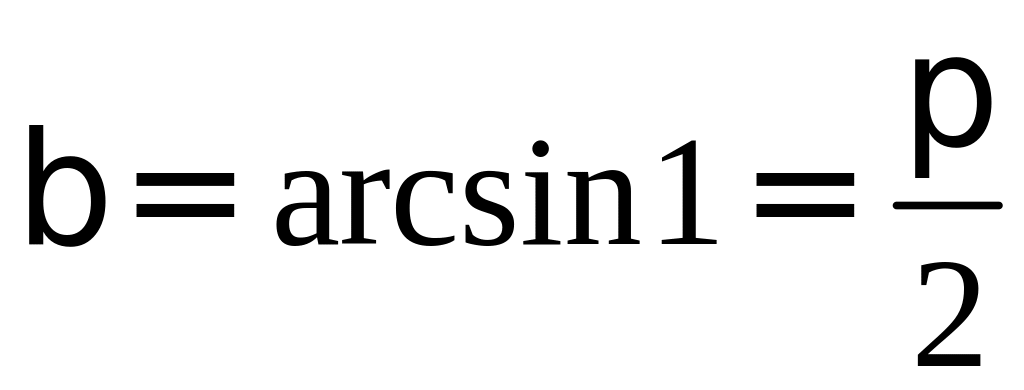, . Поэтому будем иметь:

Замечание.

При вычислении интегралов типа

.

особенно эффективны тригонометрические подстановки:

.

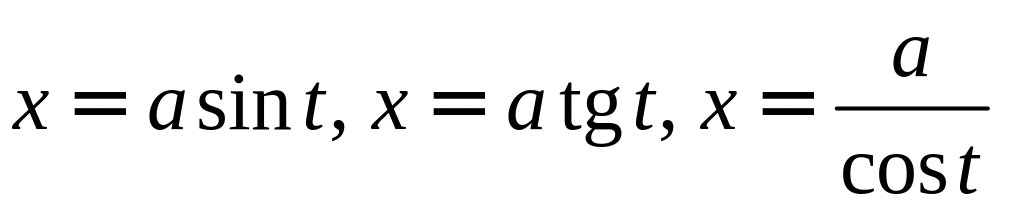. Интегрирование по частям.

Если функции и непрерывно дифференцируемы на отрезке , то

(3)

Пример 3. Найти .

Решение. Положим .

Тогда .

.

Пример 4. Найти .

Решение. Положим .

Тогда .

.

Опять интегрируем по частям:

,

.

1.3. Несобственные интегралы

. Интегралы с бесконечными пределами (несобственные интегралы первого рода).

Несобственные интегралы с бесконечными пределами определяются следующим образом:

, (4)

,

где произвольное число (обычно ).

Несобственные интегралы первого рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях равенства (4). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися.

Укажем некоторые признаки сходимости и расходимости несобственных интегралов первого рода:

1. Если на промежутке непрерывные функции и удовлетворяют условию , то из сходимости интеграла 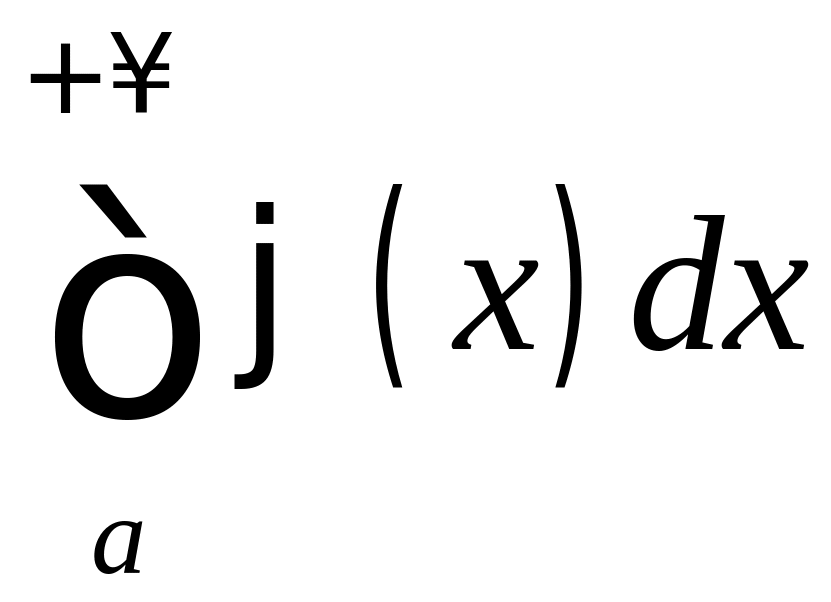следует сходимость интеграла , а из расходимости интеграла следует расходимость интеграла («признак сравнения»).

1. Если при и существует конечный предел , то интегралы и сходятся или расходятся одновременно, («предельный признак сравнения»).

Замечание.

Рассмотрим интеграл .

Если то

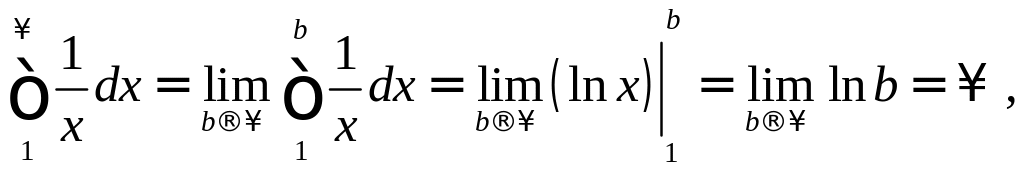
то есть при интеграл расходится.

Если тогда

Этот предел равен , если , и равен если .

Таким образом, сходится при и расходится при Поэтому в признаках сравнения в качестве функции удобно брать функцию

Пример 5. Исследовать на сходимость интеграл .

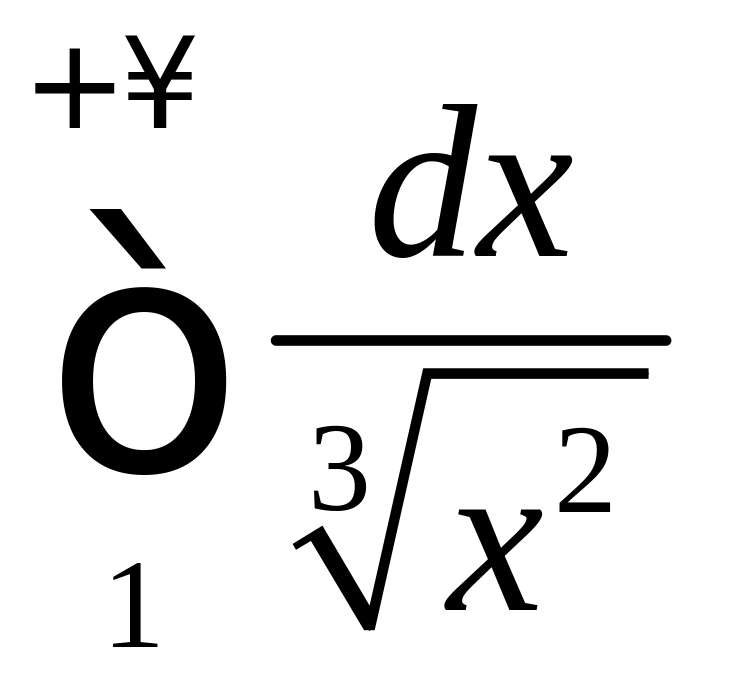Решение. Здесь при , при этом . Но интеграл расходится, .

Поэтому, согласно признаку сравнения, интеграл расходится.

Пример 6. Исследовать на сходимость интеграл .

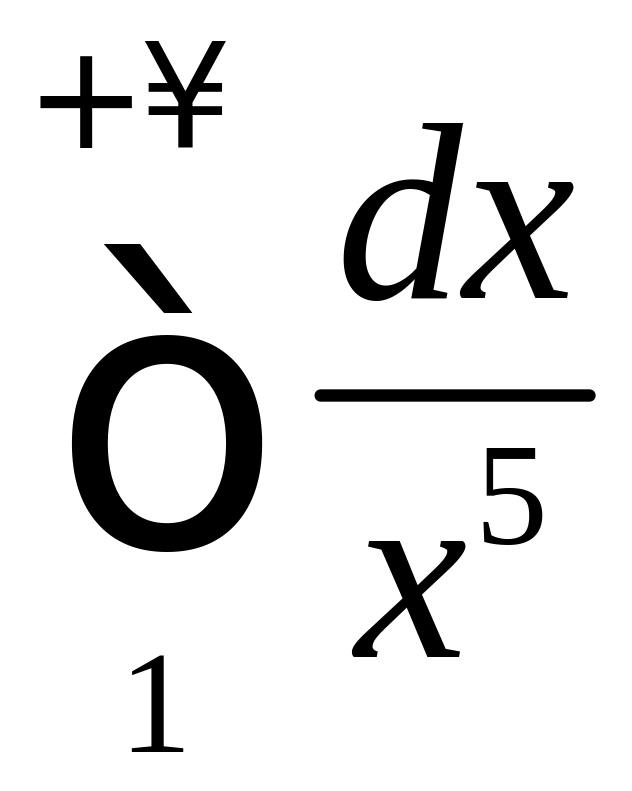Решение. Здесь . Рассмотрим функцию , интеграл от которой сходится. А так как существует предел , то исходный интеграл также сходится («предельный признак сравнения»).

Пример 7. Исследовать на сходимость интеграл .

Решение. По определению несобственного интеграла первого рода

,

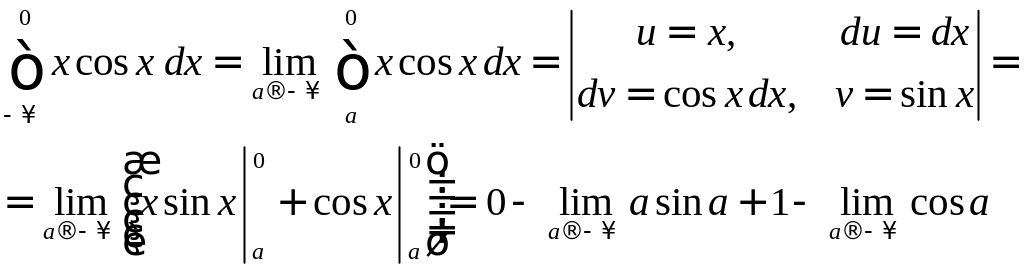интеграл расходится, т.к. не существуют.

Пример 8. Вычислить несобственный интеграл .

Решение. Подынтегральная функция определена и непрерывна на всей числовой оси. Кроме того, она является четной. Следовательно,

.

Исходя из определения несобственного интеграла, имеем

,

интеграл сходится. Следовательно, исходный интеграл также сходится и равен .

. Интегралы от неограниченных функций (несобственные интегралы второго рода).

Если функция непрерывна в промежутке и неограниченна в окрестности при любом , то несобственный интеграл от неограниченной функции определяется следующим образом:

.

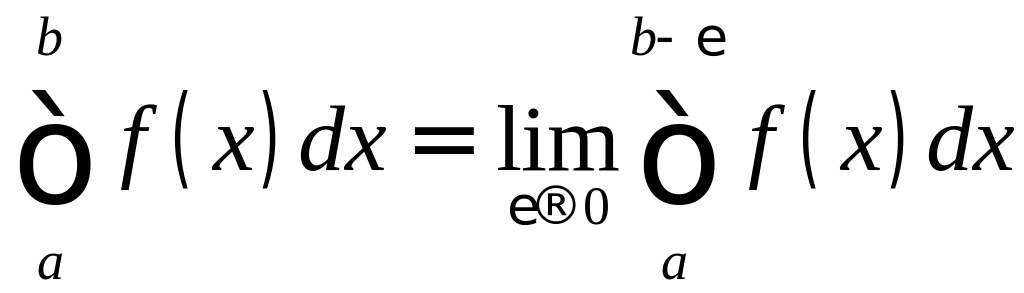Если предел, стоящий в правой части равенства, существует, то несобственный интеграл второго рода называется сходящимся; в противном случае – расходящимся.

Аналогично, если функция неограниченна в окрестности при любом , то полагают

.

Если функция неограниченна в интервале при любом и то несобственный интеграл второго рода определяется формулой

.

В этом случае интеграл называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

Укажем некоторые признаки сходимости для несобственных интегралов второго рода.

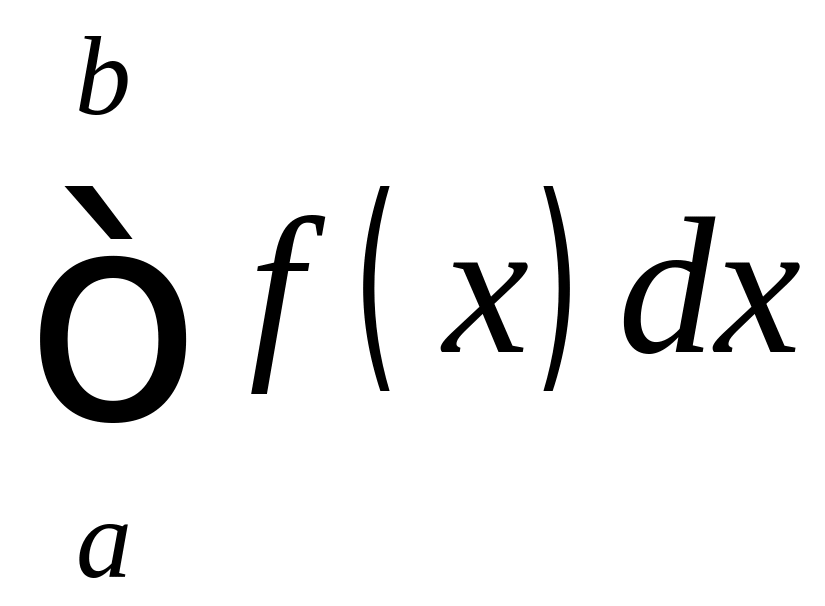1. Если на промежутке функции и непрерывны, неограниченны в интервале для любого и удовлетворяют условию , то из сходимости интеграла следует сходимость интеграла , а из расходимости интеграла следует расходимость интеграла («признак сравнения»).

2. Пусть функции и непрерывны на промежутке и в интервале неограниченны при любом . Если существует предел , то интегралы и сходятся или расходятся одновременно («предельный признак сравнения»).

Замечание. В качестве эталона для сравнения функций часто бе-

рут функцию 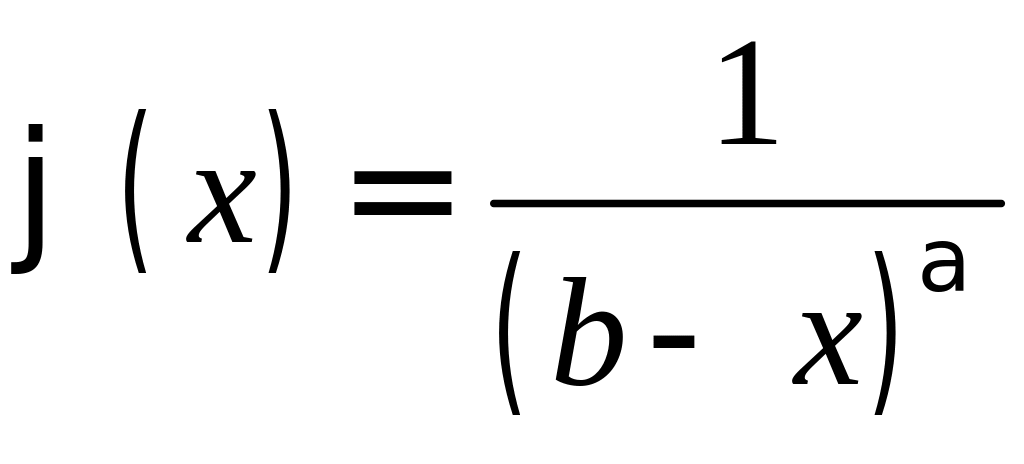. Можно показать, что несобственный интеграл

сходится при и расходится при .

Пример 9. Вычислить несобственный интеграл или установить его расходимость.

Решение. Подынтегральная функция неограниченна в окрестности точки . Так как , то

на . Здесь 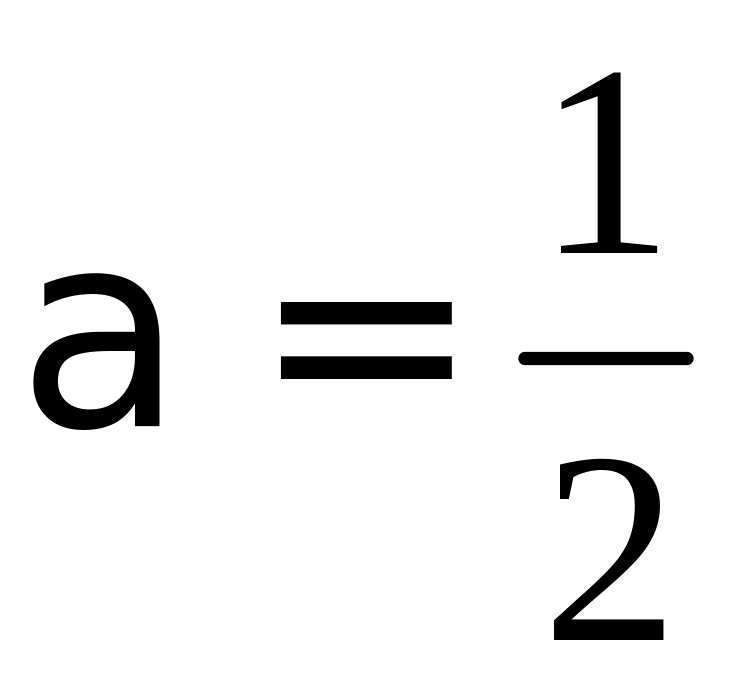, поэтому интеграл сходится. По определению имеем

.

Пример 10. Вычислить .

Решение. При функция . Интегрируя по частям, получаем

так как .

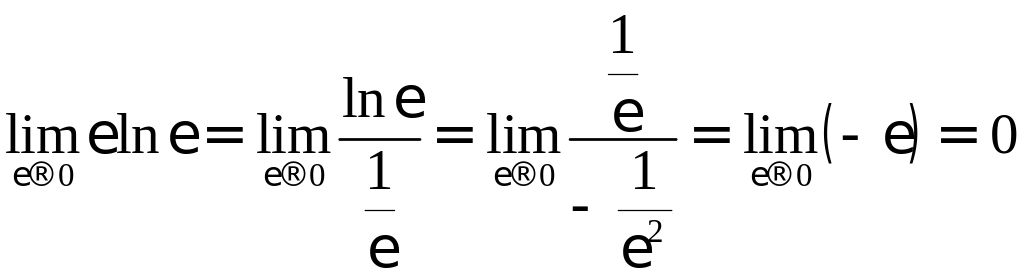Пример 11. Исследовать на сходимость .

Подынтегральная функция неограниченна на интервале для любого , и так как больше 1 то этот интеграл расходится. Если не обратить внимания на точку разрыва и формально применить формулу Ньютона –Лейбница к этому интегралу, то получили бы неверный результат: