Задание №8

Построить тело, ограниченное поверхностями.

1. x² + y² = 1, x² + y² = 27, x = 0, y = 0, z = 0 (x0, y0).

2. 4  z = x² + y², x² + y² = 4, z = 4.

3. x² + y² = 4x, z = 0, z = 2, y = 0.

4. x² + y² = 9, x  y + z = 4, z = 0.

5. x = 2y² + 1, x = 3, z = 5, z = 0.

6. x² + y² = 4y, z = 2y, z = 0.

7. y² = 4  z, x = 5, y = 0, x = 0, z = 0.

8. z = y²  6y + 9, z = 4, x = 0, x = 5.

9. x² + y² = 1, z = 2  x  y, z = 0.

10. z = y²  2y + 3, x = 0, x = 4, z = 4.

11. x = y² + 1, x + z = 3, z = 0.

12. z = x² + y², x = 2y, x = y, z = 8.

13. z =2 + y² + x², x² + y² = 4y, z = 0.

14. z + 2y = 4.

15. z = x² + y², x² + y² = 2y, x² + y² = 4y, z = 0.

16. z  2 = 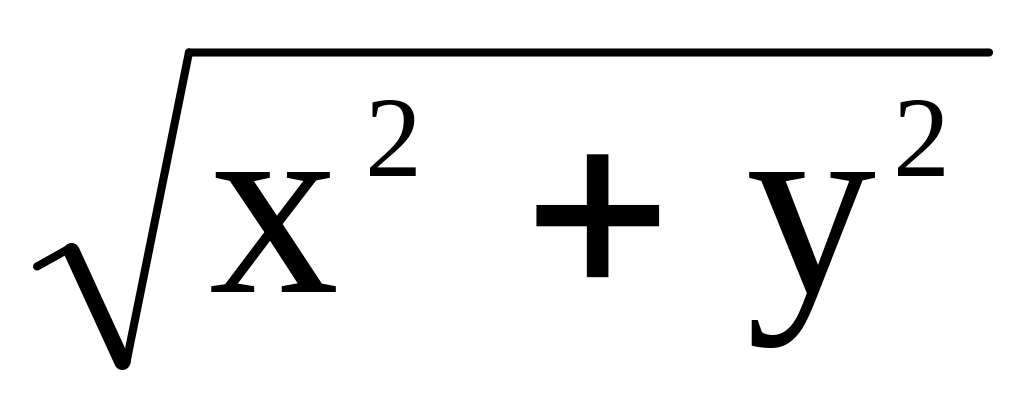, x² + y^z  6y + 5 = 0, z = 0.

17. z = 4  2x²  2y², y = x, y = 2x, z = 0.

18. y = x² + 2, y = 4, z = 0, z = 6.

19. x² + y² = 2x, z = 3x, z = 0.

20. z = 4y  y², z = 0, x = 0, x = 3.

21. x² + y² = 4x, z = 9  x²  y², z = 0.

15. y = 2z, y = 0, x = 0, z = 0.

16. 3x = z.

17. z = x² + y²  6y + 11, z = 11.

18. z = 2  x²  y² + 2y, z = 0.

19. x + y = 6, y = x, z = 4y, z = 0.

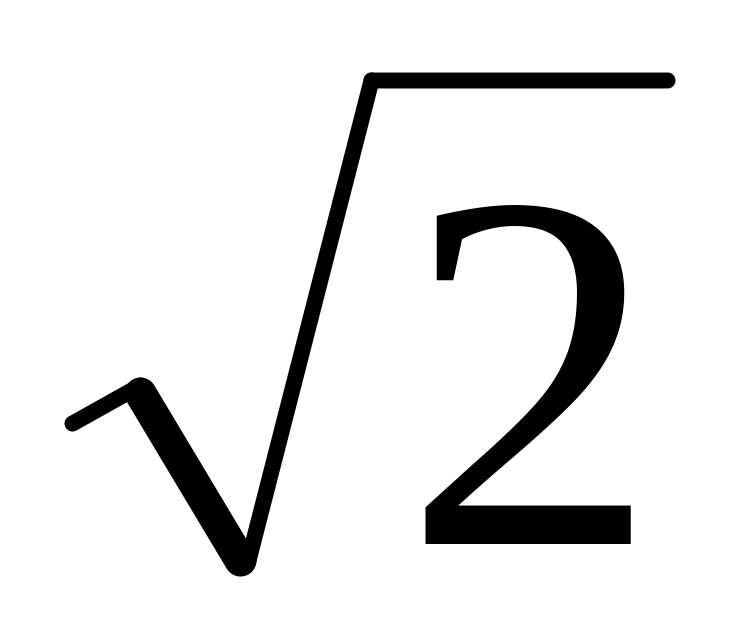20. x = y, x = 2 y, z + y = 2, z = 0.

21. x + y = 4, y = x, z = 0, z = 3y.

22. x² + y² = 2y, x² + y² = 4y, , z = 0.

23. x² + y² = 4x, z = 12  y, z = 0.

III. Примеры решения задач

Задание №1.

Вычислить производные первого и второго порядка от заданной функции z = x² + y² + xy  cos(3xy  2).

Решение.

При вычислении частной производной по переменной x переменную y рассматриваем как постоянную величину. Пользуясь правилами дифференцирования функции одной переменной и, в частности, правилом дифференцирования сложной функции, получаем

Аналогично поступаем при вычислении частной производной по переменной y. Считая x постоянной величиной, получаем

Используя те же правила, вычисляем частные производные второго порядка: