Метод Фибоначчи с запаздываниями (Lagged Fibonacci generator)

Этот метод рекомендуется сейчас для получения генерации псевдослучайных чисел в статистических алгоритмах, критичных к качеству случайных чисел.

Наибольшую популярность фибоначчиевы датчики получили в связи с тем, что скорость выполнения арифметических операций с вещественными числами сравнялась со скоростью целочисленной арифметики, а фибоначчиевы датчики естественно реализуются в вещественной арифметике.

Один из широко распространённых фибоначчиевых датчиков основан на следующей итеративной формуле:

если и если

(2.4)

где — вещественные числа из диапазона [0; 1), a, b — целые положительные числа, называемые «лагами». Для работы фибоначчиеву датчику требуется знать max(a, b) предыдущих сгенерированных случайных чисел. При программной реализации для хранения сгенерированных случайных чисел используется конечная циклическая очередь на базе массива. Для старта фибоначчиевому датчику требуется max(a, b) случайных чисел, которые могут быть генерированы простым конгруэнтным датчиком.

Лаги a и b — «магические» и их не следует выбирать произвольно. Рекомендуются следующие значения лагов: a = 55, b = 24; a = 17, b = 5; a = 97, b = 33. Качество получаемых случайных чисел зависит от значения константы, a чем оно больше, тем выше размерность пространства, в котором сохраняется равномерность случайных векторов, образованных из полученных случайных чисел. В то же время, с увеличением величины константы a увеличивается объём используемой алгоритмом памяти.

Значения a = 17, b = 5 можно рекомендовать для простых приложений, не использующих векторы высокой размерности со случайными компонентами. Значения a = 55, b = 24 позволяют получать числа, удовлетворительные для большинства алгоритмов, требовательных к качеству случайных чисел. Значения a = 97, b = 33 позволяют получать очень качественные случайные числа и используются в алгоритмах, работающих со случайными векторами высокой размерности. Описанный фибоначчиев датчик случайных чисел (с лагами 20 и 5) используется в широко известной системе Matlab.

3 Преобразование случайных величин

Для статистической имитации необходимо уметь получать случайные числа с заданным законом распределения. Любой закон распределения может быть получен из равномерного на интервале (0; 1).

Получение (разыгрывание) дискретной случайной величины

Значения случайной величины и вероятности их реализации представим в виде таблицы:

Соотношение (1.4) позволяет разбить интервал (0,1) на интервалов, так что длина каждого интервала равна вероятности реализации соответствующего значения .(рис. 3.1). Такое разбиение предоставляет следующий способ получения распределения дискретной случайной величины с помощью равномерного распределения на интервале (0,1).

Берётся случайное число из равномерного распределения на интервале (0,1) и определяется, в какой из интервалов это число попало. Если оно попало в интервал с номером , то случайной величине приписывается значение Затем берётся новое число из равномерного распределения, и вся процедура повторяется.

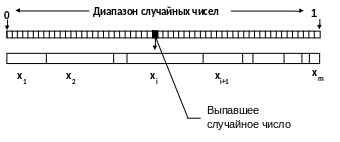
Рис. 3.1. Способ реализации заданного распределения случайной величины разыгрыванием