Вариационный ряд, диаграмма накопленных частот и гистограмма выборки

Пусть имеется набор (выборка) экспериментальных данных x₁, x₂, …, x_n. Вариационный ряд (или ряд распределения) z₁, z₂, …, z_n получают из исходных данных путем расположения x_m (m=1,2, …,n) в порядке возрастания от x_min до x_max.

Например, пусть имеется выборка объема 5:

x₁=5, x₂=2, x₃=4, x₄=5, x₅=7.

Вариационный ряд для данной выборки будет таким:

z₁=2, z₂=4, z₃=5, z₄=5, z₅=7.

Диаграмма накопленных частот P_n(x) является эмпирическим аналогом интегрального закона распределения P(X) и ее строят в соответствии с формулой

где μ_n(x) – число элементов в выборке, для которых значение x_i < x.

Стоится диаграмма накопленных частот следующим образом. На оси абсцисс указывают значения наблюдений x_m (или z_m). Значение по оси ординат равно нулю левее точки x_min; в точке x_min и далее во всех других точках x_m диаграмма имеет скачок, кратный 1/n. Если существует k совпадающих значений x_m, то в этом месте на диаграмме происходит скачок, равный k/n. Таким образом, в точке x = x_max значение диаграммы накопленных частот достигает 1. Отметим, что если n→∞, то P_n(x) → P(x).

Для рассмотренной выше выборки из пяти элементов диаграмма накопленных частот выглядит следующим образом.

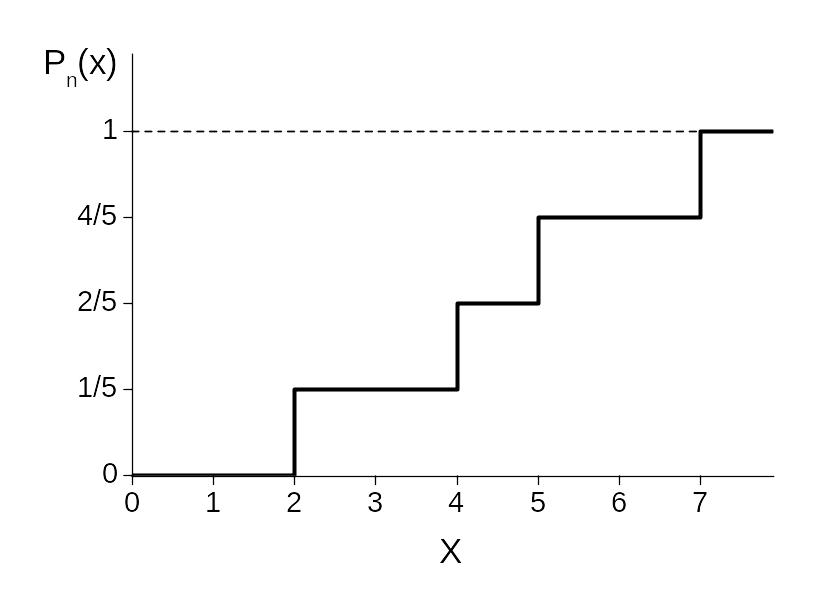
Рис.1. Диаграмма накопления частот

Гистограмма выборки f_n(x) является эмпирическим аналогом функции плотности распределения f(x). Она позволяет наглядно изобразить распределение случайной величины.

Последовательность построения гистограммы такова. Диапазон изменения случайной величины (x_min; x_max) разбивается на некоторое количество N (обычно 10-20) частей (или промежутков). Гистограмма, составленная на основе разбиения со слишком маленькими интервалами, обычно многовершинная и не отражает наглядно существенных свойств распределения. С другой стороны, разбиение по слишком крупным интервалам может привести к потере ясного представления о характере распределения. Желательно разбивать так, чтобы в один такой промежуток попало хотя бы одно выборочное значение x_i, но и не более 15−20 % всех значений.

Далее определяют длину таких промежутков (интервалов):

Δx = (x_max − x_min)/N

Середину области изменения выборки (центр распределения)

(x_max − x_min)/2

принимают за центр некоторого промежутка, после чего находят границы и окончательное количество указанных интервалов так, чтобы в совокупности они перекрывали всю область от x_min до x_max. Далее подсчитывают количество попавших в данный промежуток случайных величин k(x_m) и нормируют на число элементов в выборке n

k(x_m)/n

Наконец, строят гистограмму, представляющую собой ступенчатую кривую, значение которой в пределах m-го интервала (x_m, x_m + Δx) (m = 1, 2, …, N) постоянно и равно k(x_m)/n. Зачастую гистограмму изображают не в виде ступенчатой кривой, а с помощью столбцов (Рис. 2).

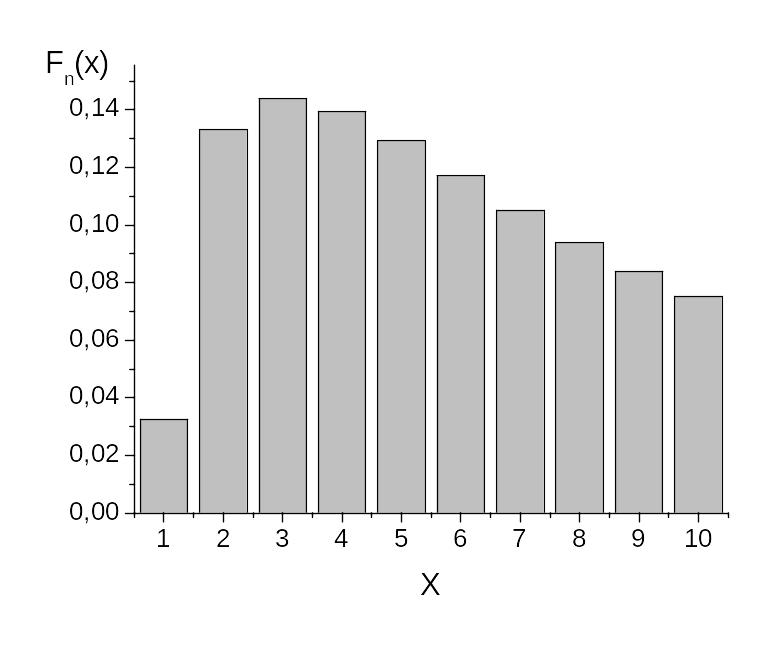
Рис.2. Гистограмма выборки

2. Алгоритмы моделирования случайных чисел Линейный конгруэнтный метод.

Чтобы получить представление о свойствах функции , попытаемся представить вид её графика на плоскости (x, y) Будем для определённости иметь в виду равномерное распределение случайных чисел на отрезке Тогда график функции будет расположен внутри квадрата со стороной равной единице (Рис.1). По обеим осям будут отложены фактически одни и те же равномерно распределённые точки. Это означает, что график должен как можно более равномерно заполнять квадрат 1×1.

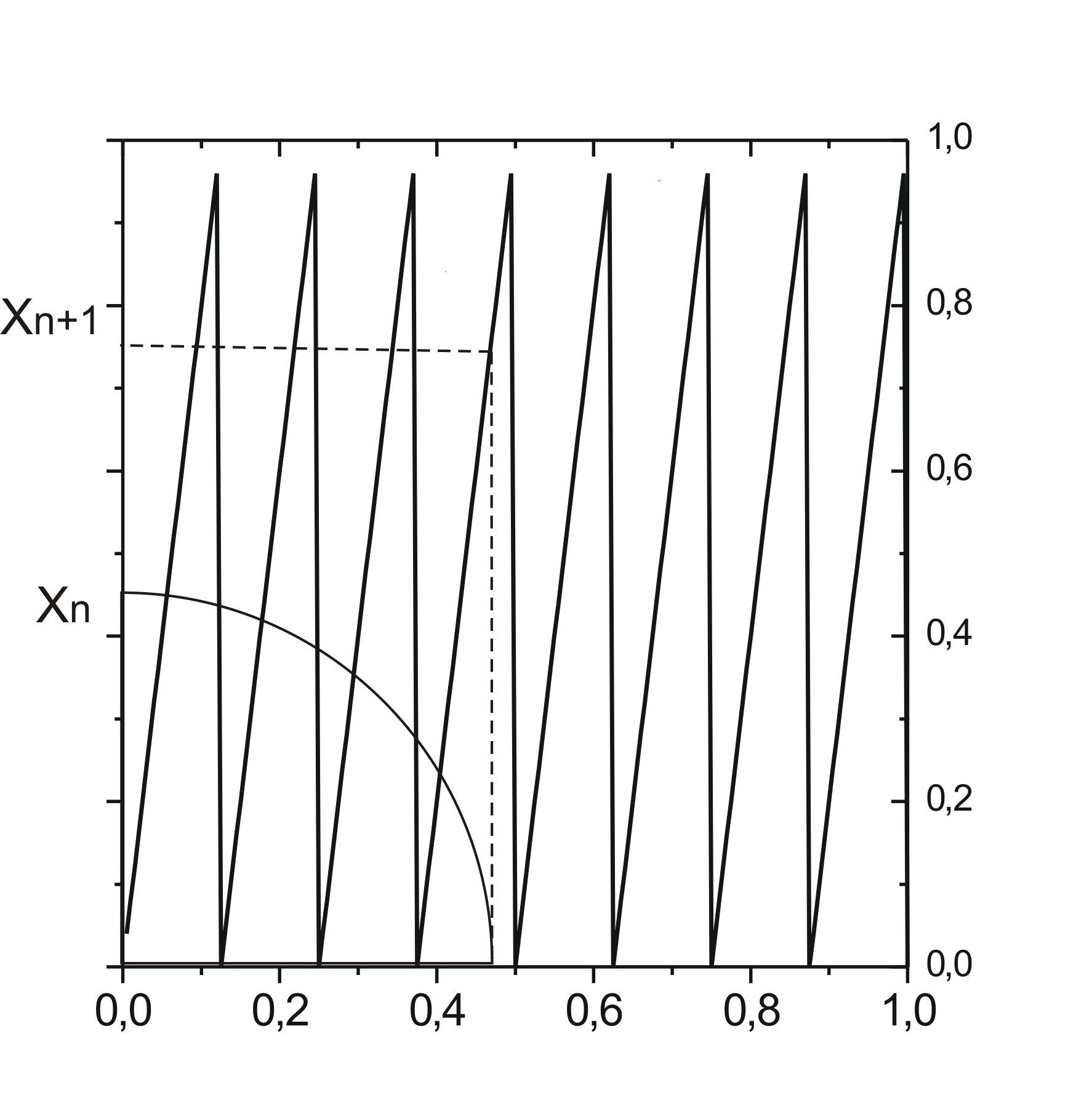
Рис. 2 Функция

Оказывается, очень просто можно получить функцию, обладающую таким свойством. В частности, им обладает функция:

(2.1)

Здесь значок означает дробную часть. Рис. 2, построенный для m=8 поясняет принцип алгоритма (2.1). На самом деле, надо использовать в качестве – большое число. На этой идее основан метод получения случайных чисел, предложенный Д. Лемером. Сейчас он чаще всего называется «линейный конгруэнтный метод». Его исследованию посвящена обширная литература.

Наиболее часто линейный конгруэнтный метод применяется в следующем виде: Выбирают четыре целых положительных числа:

1. Множитель a;

2. Сдвиг c;

3. Модуль m;

4. Первое число последовательности x₀.

Последовательность случайных чисел определяется формулой:

(2.2)

где индекс n пробегает значения 0, 1, 2, ... Символ b mod m означает остаток от деления числа b на m. Очевидно, что b mod m < m. Поэтому все числа последовательности x_n удовлетворяют неравенству x_n < m. Последовательность чисел y_n, равномерно распределенных в интервале от нуля до единицы, получается по формуле:

(2.3)

Далеко не любой выбор четырех исходных чисел ведет к хорошим результатам. Заметим прежде всего, что последовательность чисел x_n неизбежно должна быть периодической, причем период не может быть больше, чем m. Действительно, так как все x_n – целые числа, причем x_n < m, количество различных чисел не может превышать m. Поэтому, начиная, по крайней мере, с n = m, появится число, которое уже встречалось, и все повторится заново.

Однако получить последовательность с максимально возможным периодом L = m далеко не просто. Если выбирать исходные числа не задумавшись, то, как правило, будут получаться последовательности с маленьким периодом.

Итак, чтобы получить генератор с максимально возможным периодом L, нужно взять в качестве m самое большое число, с которым может оперировать данная ЭВМ, и выбрать остальные числа в соответствии с следующей теоремой.

Теорема. Если последовательность определяется формулой (2.2) с c ≠ 0, то ее период равен m тогда и только тогда, когда выполнены следующие условия:

а) c и m – взаимно простые числа (не имеют общих делителей, кроме единицы);

б) b = k–1 кратно p для любого простого числа p, являющегося делителем m;

в) b кратно 4, если m кратно 4.

Разработана сложная система тестов, которая позволяет определить качества генератора случайных чисел. Поэтому рекомендуется использовать только проверенные генераторы. При выборе генератора свойства ЭВМ важны не только для того, чтобы выбрать максимально возможный период. От выбора параметров генератора зависит скорость генерации случайных чисел. При этом оказывается, что для ЭВМ разных конструкций оптимальными являются разные генераторы. В частности, приводятся данные для генератора, работающего на основе линейного конгруэнтного метода с периодом 2³⁸ ≈ 2,75 × 10¹¹.

За последнее время получили распространение генераторы случайных чисел, основанные на другой идее.