В. Сложные экспертизы. Метод дерева целей

Сложные экспертизы находят широкое применение при прогнозировании и планировании в экономике, политике, широкомасштабных научных исследованиях и т.п. Как правило, они не дают прямых указаний о предпочтительности выбора того или иного решения и не оценивают последствия различных решений. Главным предназначением сложных экспертиз является оценка осуществимости тех или иных явлений и событий, а также определение их вероятных сроков и последовательности свершения. Располагая информацией такого рода, ЛПР может найти решения, способствующие (или – при необходимости – препятствующие) появлению анализируемых событий. Вследствие чрезвычайной сложности исследуемых явлений и – как правило – их значительной удаленности во времени от проводимой экспертизы, намного более корректно говорить о вероятностях (шансах) реализации того или другого явления, а не о конкретных сроках его реализации.

Следует отметить, что к строгому математическому понятию вероятности экспертные оценки такого рода можно отнести лишь условно, т.к. речь идет не о массовых событиях, а, как правило, об уникальных. В связи с этим указанные экспертные оценки получили название интуитивных вероятностей. Интуитивные вероятности представляют собой своеобразную форму нечеткого представления экспертных оценок сложных ситуаций. Следует отметить, что нестрогость понятия интуитивной вероятности не означает ее “неполноценности” и ее использование дает результаты, хорошо согласующиеся с реальностью. Исчисление интуитивных вероятностей проводится по используемым в теории вероятностей правилам.

Использование экспертами интуитивных вероятностей вызывает необходимость формулировки самих вопросов в вероятностном смысле. Например, вместо вопроса “Когда произойдет событие?”, следует задать вопрос “Какова вероятность того, что событие произойдет до какого-то момента времени?”. Следует отметить, что часто даже в данной постановке эксперт или эксперты не в состоянии дать достаточно обоснованный ответ. В таких случаях проводят декомпозицию (расчленение) анализируемых явлений и событий на более простые, оценка которых не столь сложна. Далее обрабатывают полученные от экспертов оценки и на ее основе пытаются ответить на вопрос.

Таким образом, в основе сложных экспертиз лежит декомпозиция исходной сложной проблемы на составляющие, проведение по ним совокупности простых экспертиз с последующей обработкой полученных экспертных оценок. В настоящее время существует несколько типов сложных экспертиз, например, метод дерева целей, метод решающих матриц, метод “Дельфи” и ряд других. Мы ограничимся рассмотрением сложной экспертизы “Метод дерева целей”.

Исследуемое событие обозначим как и назовем заключительным. Группа экспертов должна произвести декомпозицию данного события на составляющие и определить, таким образом, дерево целей. При этом каждый член экспертной группы должен указать промежуточные события , от реализации которых зависит осуществление события . Следует отметить, что нумерация событий при этом никак не связана с очередностью их реализации, важностью и прочими характеристиками. Неосуществление любого из них делает невозможным осуществление заключительного события. Часто для обеспечения полноты перечня событий в состав экспертной группы привлекаются специалисты различного профиля.

Как правило, события также оказываются сложными для непосредственной оценки экспертами и, в свою очередь, могут быть представлены как результат осуществления других, более простых событий , где первый индекс указывает на связь перечисленных событий с событием , а второй - является номером события в связке. Назовем события промежуточными событиями первого уровня; - промежуточными событиями второго уровня . Если экспертные оценки промежуточных событий второго уровня получить также затруднительно, то процесс декомпозиции продолжается и вводятся события третьего, четвертого и т.д. уровней.

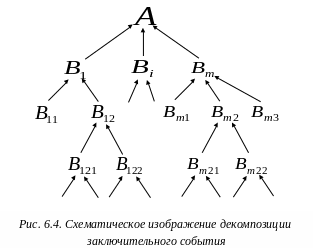
Полученные в результате декомпозиции исходного события результаты представляют графически, причем события изображаются кружками, а связи между событиями – стрелками. В результате получается граф событий (Рис.6.4), по виду напоминающий перевернутое дерево (отсюда – дерево целей).

После формирования дерева целей экспертам необходимо оценить безусловные интуитивные вероятности событий, находящихся на нижних уровнях. Эти оценки используются для расчета вероятности того, что к назначенному сроку реализуется заключительное событие . Расчет осуществляется на базе основных теорем теории вероятностей.

Анализ дерева целей позволяет сделать вывод о том, что заключительное событие является некоторой комбинацией промежуточных состояний первого уровня, что можно представить следующим равенством:

(6.15)

Вид функции определяется характером логической взаимосвязи заключительного события с промежуточными . Событие осуществится, если реализуется каждое из промежуточных событий . Поэтому:

.

Так как события реализуются независимо друг от друга, то, согласно теореме о вероятности произведения независимых событий получим:

(6.16)

Далее мы можем записать систему соотношений вида:

, (6.17)

в которых функция учитывает взаимосвязь событий первого уровня с соответствующими событиями второго уровня. Предположим, что в рассматриваемом нами случае событие осуществится, если произойдет хотя бы одно из событий . При этом предположении:

Так как события , вообще говоря, совместны, то для расчета вероятности события удобно перейти к противоположным событиям:

,

где учтено, что событие, противоположное сумме событий, равно произведению противоположных событий.

Обычно работы по реализации программ, приводящих к событиям типа , осуществляются независимо друг от друга, вследствие чего события являются независимыми. В связи с этим на основании теоремы о вероятности произведения независимых событий получим:

,

или, используя свойство вероятности противоположного события,

.

Действуя аналогичным образом, можно выразить все остальные вероятности событий первого уровня через вероятности связанных с ними событий второго уровня.

Вычисления производятся до тех пор, пока вероятность не будет выражена через вероятности событий самых нижних уровней.

Помимо вероятностных характеристик событий с помощью дерева целей могут быть оценены временные затраты, стоимостные и другие показатели реализации соответствующих событию программ (проектов).

Достоинством метода дерева целей является наглядность взаимосвязей между составляющими исследуемой сложной проблемы. Для реализации экспертизы необходимо привлекать большое число экспертов различных специальностей. Поэтому деятельность соответствующих экспертных групп должна быть надлежащим образом организована. С этой целью по указанию ЛПР создается специальная экспертная группа со следующими функциями:

• Осуществление предварительного анализа сложной проблемы и декомпозиция проблемы на составляющие;

• Формирование экспертных групп для уточнения первоначального варианта расчленения, формулировки вопросов для экспертов и определения методики проведения простых экспертиз по каждому из вопросов;

• Определение первоначального состава экспертных групп для проведения всех простых экспертиз;

• Проведение совокупности простых экспертиз;

• Предварительный анализ экспертных оценок и проведение в случае необходимости дополнительных туров экспертного оценивания;

• Обработка результатов и выработка рекомендаций для ЛПР.