Квадратичный выбор.

Рассмотрим следующий метод: пусть файл содержит 16 записей. Разобьём его на четыре группы по четыре записи.

|| 14 5 18 21 || 2 7 11 3 || 9 26 1 8 || 13 22 6 20 ||

Найдём наибольшие элементы в каждой группе и соберём их вместе:

21 11 26 22

Тогда наибольший среди них и будет наибольшим в файле. Чтобы получить второй по величине элемент, достаточно просмотреть оставшиеся элементы группы, содержащей 26, т.е. максимальный, и максимум из них поместить в «группу лидеров» на место 26 и т.д.

Вообще, если N - точный квадрат, то можно разделить файл на √N групп по √N элементов в каждой. Тогда любой шаг, кроме первого, потребует не более, чем √N – 1 сравнений внутри группы раннее выбранного элемента плюс √N – 1 сравнений в “группе лидеров”. Этот метод получил название “квадратичный выбор”.

Оказывается такой метод может быть обобщён: существует метод кубического выбора (³√N больших групп, каждая из которых содержит ³√N малых групп по ³√N записей), выбора четвёртой степени и т.д. Если эту идею развить до её полного логического завершения, то мы придём к выбору n-й степени, основанному на структуре бинарного дерева.

Пример: Схема кубического выбора.

(n=27, ³√27=3);

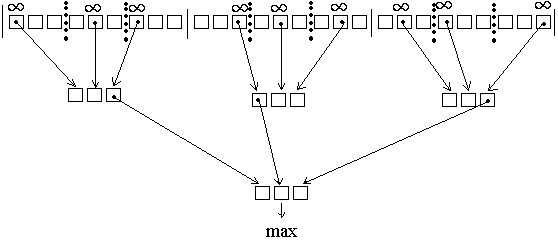
max –максимальный элемент в выходную последовательность

Выбор из дерева

Этот метод является выбором n-й степени, где n выбрано так, что размер самой малой группы минимален и равен 2.

i j Рассмотрим, например, результаты соревнований по настольному теннису:

Р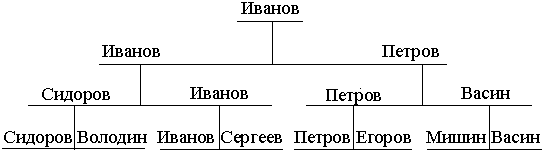 ис. 3 – Дерево выбора

Сидоров побеждает Володина, а Иванов побеждает Сергеева; затем в следующем туре Иванов выигрывает у Сидорова и т.д.

На этом рисунке показано, что Иванов – чемпион среди восьми спортсменов, а для того, чтобы определить это, потребовалось 8-1=7 матчей (т.е. сравнений).

Петров вовсе не обязательно будет вторым по силе игроком: любой из спортсменов, у которых выиграл Иванов (чемпион), включая даже проигравшего в первом туре Сергеева, мог бы оказаться вторым по силе игроком. Второго игрока можно определить, заставив сыграть Сергеева с Сидоровым, а победителя этого матча – с Петровым. Всего два матча требуется для определения второго по силе игрока, исходя из того соотношения сил, которое мы запомнили из предыдущих игр.

Метод сортировки простым выбором основан на повторном выборе наименьшего ключа среди n элементов, затем среди n-1 элементов и т.д. Поиск наименьшего ключа из n элементов потребует n-1 сравнений, из (n-1) элементов – (n-2) сравнений.

Как можно улучшить эту сортировку выбором? Это можно сделать только в том случае, если получить от каждого прохода больше информации, чем просто указание на один наименьший элемент.

Например, с помощью n/2 сравнений можно определить наименьший элемент (ключ) из каждой пары, при помощи n/4 сравнений можно выбрать наименьший из каждой пары таких наименьших ключей и т.д. Наконец, при помощи n-1 сравнений можно построить дерево выбора и определить корень как наименьший ключ.

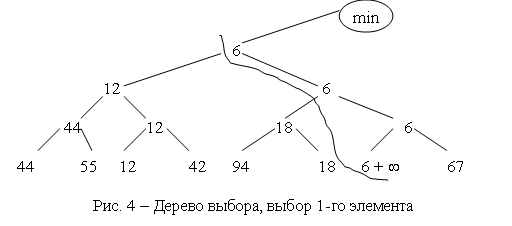
На втором шаге нужно спуститься по пути, указанному наименьшим ключом, и исключить его, последовательно заменяя либо на “дыру” (или ключ ∞), либо на элемент, находящийся на противоположной ветви промежуточного узла.

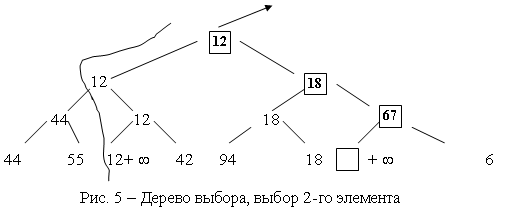
Элемент, оказавшийся в корне дерева, вновь имеет меньший ключ (среди оставшихся) и может быть исключён.

После n таких шагов дерево становится пустым (т.е. состоит из “дыр”) и процесс сортировки закончен.

Каждый из n шагов требует log₂n сравнений. Вся сортировка требует порядка n*log₂n элементарных операций, не считая n шагов которые необходимы для построения дерева.

Это значительное улучшение по сравнению с простым методом, требующим n² шагов. При сортировке с помощью дерева задача хранения информации стала сложнее и поэтому увеличилась сложность отдельных шагов. Для хранения возросшего объёма информации, получаемой на начальном проходе, нужно строить некоторую древовидную структуру.

Сортировка слиянием

Слияние – означает объединение двух или более упорядоченных файлов в один упорядоченный файл.

Можно, например, слить два подфайла,

1-й – 3 6 11 21 30

2-й - 1 4 7 9 28

получив 1 3 4 6 7 9 11 21 28 30.

Простой способ сделать это – сравнить два наименьших элемента, вывести наименьший из них и повторить процедуру.

Н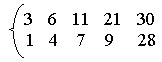 ачав с

п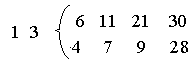 олучим

затем

и т.д.

Самый простой алгоритм здесь – двухпутевое слияние.

Алгоритм.(Двухпутевое слияние).

Этот алгоритм осуществляет слияние двух упорядоченных файлов x₁≤ x₂≤…≤x_m и y₁≤y₂≤…≤y_n в z₁≤z₂≤…≤z_m+n.

М1. [Начальная установка.] Установить i←1, j←1,k←1.

М2. [Найти наименьший элемент.] Если x_i≤y_j, то перейти к шагу

М3, в противном случае перейти к шагу М5.

М3. [Вывести x_i] Установить z_k←x_i, k←k+1, i←i+1. Если i≤m, то

возвратиться к М2.

М4. [Вывести y_j,…,y_n.] Установить (z_k,…,z_m+n)←(y_j,…,y_n) и завершить

работу алгоритма.

М5. [Вывести y_j.] Установить z_k←y_j,k←k+1,j←j+1. Если j≤n, то

возвротиться к М2.

М6. [Вывести x_i,…,x_m] Установить (z_k,…,z_m+n)←(x_i,…,x_m) и

завершить работу алгоритма.

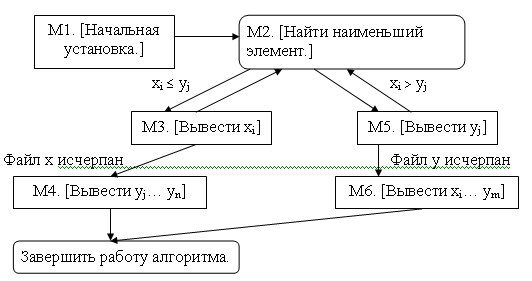
Рис. 6 – Алгоритм “Двухпутёвое слияние”

Общий объём работы, выполняемой алгоритмом М, по существу пропорционален m+n (отсюда слияние – более простая задача, чем сортировка). Задачу сортировки можно свести к слияниям, сливая всё более длинные подфайлы до тех пор, пока не будет отсортирован весь файл. Такой подход можно рассматривать как развитие идеи сортировки вставками: вставки нового элемента в упорядоченный файл – частный случай слияния при n=1

.