2.2. Транспортная задача линейного программирования

Стандартная транспортная задача определяется как задача разработки наиболее экономичного плана перевозки продукции однородного груза из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Исходные параметры модели транспортной задачи

n – количество пунктов отправления;

m – количество пунктов назначения;

Qi – запас в пункте отправления Ai (i = 1,2…n);

bj – спрос на продукцию в пункте назначения Bj (j = 1,2…m);

Cij – тариф (стоимость) перевозки единицы продукции из пункта отправления Ai в пункт назначения Bj;

Xij – количество продукции, перевозимой из пункта отправления Ai в пункт назначения Bj;

F(х) – транспортные расходы на перевозку всей продукции (р.).

Транспортная модель

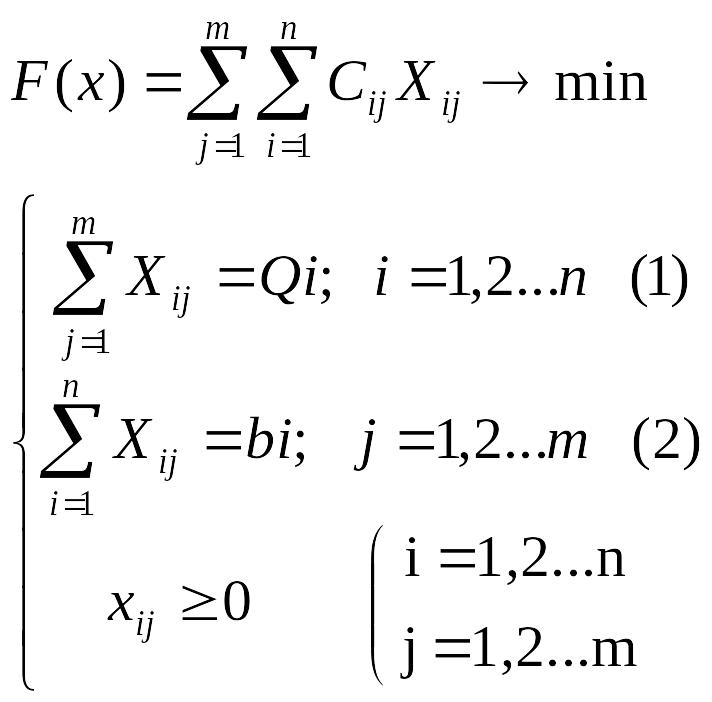
Целевая функция представляет собой общие транспортные расходы на осуществление всех перевозок в целом.

Первая группа (1) ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта.

Вторая группа (2) ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворять спрос на продукцию в этом пункте. Наглядной формой транспортной задачи является транспортная матрица.

Общий вид транспортной матрицы

Пункты отправления Ai	Пункты потребления				Запасы Qi
	B1	B2	…	Bm
A1	C11 X11	C12 X12	…	C1n X1m	Q1
A2	C21 X21	C22 X22	…	C2n X2m	Q2
…	…	…	…	…	…
An	Cn1 Xn1	Cn2 Xn2	…	Cnm Xnm	Qn
Потребн. bj			…

Из модели следует, что сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, т.е.

Если это условие выполняется, то транспортная задача называется закрытой, а в противном случае - открытой.

Рассмотрим вариант стандартной транспортной задачи

Пример. С двух складов нужно перевезти однородный груз в три магазина.

На I складе имеется 1800 т груза;

На II складе имеется 2600 т груза.

В магазин № 1 нужно доставить 1000 т;

В магазин № 2 нужно доставить 1200 т;

В магазин № 3 нужно доставить 2200 т.

Таблица - Тариф (стоимость) перевозки 1 т груза, тыс. руб.

Склады	магазины
	№1	№2	№3
I	2	2	3
II	3	4	2

Требуется определить такой план перевозок, при котором весь груз будет доставлен в указанных количествах в каждый магазин с минимальными затратами на перевозку.

Обозначим Xij – количество груза, которое необходимо перевезти от i – го поставщика (склада) к j – му потребителю (магазину)

i = 1,2

j = 1,2,3.

X₁₁ – объем груза, перевозимого c I склада в магазин № 1, т;

Х₁₂ - объем груза, перевозимого cо II склада в магазин № 2, т;

Х₁₃ - объем груза, перевозимого c III склада в магазин № 3, т;

Х₂₁ - объем груза, перевозимого cо II склада в магазин № 1, т;

Х₂₂ - объем груза, перевозимого cо II склада в магазин № 2, т;

Х₂₃ - объем груза, перевозимого cо II склада в магазин № 3, т.

Ограничения:

1. по возможности I склада, т х₁₁ + х₁₂ + х₁₃ = 1800

2. по возможности II склада, т х₂₁ + х₂₂ + х₂₃ = 2600

3. по потребности магазина № 1, т х₁₁ + х₂₁ = 1000

4. по потребности магазина № 2, т х₁₂ + х₂₂ = 1200

4400 т = 4400 т

Целевая функция

F(x) = 2х₁₁ + 2х₁₂ + 3х₁₃ + 3х₂₁ + 4х₂₂ + 2х₂₃ →min

Решение:

Вначале принимается исходный вариант перевозок, а затем последовательно производится его улучшение до получения оптимального плана.

Для получения первоначального исходного плана перевозок используем правило «северо-западного» угла, т.е. вначале максимально допустимое количество груза помещается в верхнюю левую клетку 91 строка 1 столбец, затем заполняется соседняя клетка и т.д. до распределения всего количества груза.

При этом количество занятых клеток составит:

m + n – 1 = 2 + 3 – 1 = 4 , где

m – количество поставщиков:

n – количество потребителей.

Первоначальный план представлен в следующей таблице:

Склады	магазины			Запас Qi
	№1	№2	№3
I	2 1 000	2 8 00	3	1800
II	3	4 400	2 2200	2600
Спрос bj	1000	1200	2200	4400=4400

х₁₁ = 1000 т х₂₂ = 400 т

х₁₂ = 800 т х₂₃ = 2200 т

F (x) = 2*1000 + 2*800 + 4*400 + 2*2200 = 9600 т. р