2. Методические рекомендации по выполнению заданий контрольной работы

2.1. Симплекс-метод решения задач линейного программирования

Симплексный метод основан на последовательном переходе от одного опорного плана задачи линейного программирования к другому, при этом значение целевой функции изменяется.

Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота.

Коммерческое предприятие реализует “n” товарных групп, располагая “m” ограниченными материально-денежными ресурсами в_i 0 (i= 1, 2, …..m). Известны расходы ресурсов каждого i–го вида на реализацию единицы товара по каждой группе, представленной в виде матрицы А=(а_ij), и прибыль “Cj”, получаемая предприятием от реализации единицы товара “j” группы. Надо определить объем и структуру товарооборота “хj” (j = 1, 2, … ,n), при которых прибыль коммерческого предприятия была бы максимальной.

Математическую модель задачи запишем следующим образом. Определить вектор Х =(х₁, х₂, …х_n), который удовлетворяет ограничениям вида:

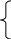
a_ij * х_j в_i, i = 1,2 …m (1)

х_j 0, j = 1,2 …..n (2)

и обеспечить максимальное значение целевой функции

f(х) = Сj * Хj mах (3)

Пример: Коммерческое предприятие, располагающее материально-денежными ресурсами, реализует три группы товара А, В и С. Плановые нормативы затрат ресурсов на 1 тыс. руб. товарооборота, доход от продажи товаров на 1 тыс. руб. товарооборота, а также объем ресурсов заданы в следующей таблице:

Виды материально-денежных ресурсов	Норма затрат материально-денежных ресурсов на 1 тыс. руб. товарооборота			Объем ресурсов (вi)
	группа А	группа В	группа С
Рабочее время продавцов, чел-ч	0,1	0,2	0,4	1 100
Площадь торговых залов, м2	0,05	0,02	0,02	120
Площадь складских помещений, м2	3	1	2	8 000
Доход, тыс. руб. (Сj)	3	5	4	mах

Определить плановый объем продажи товаров так, чтобы доход торгового предприятия был максимальный.

Переменные:

х₁ – количество товаров группы А, ед.

х₂ – количество товаров группы В, ед.

х₃ – количество товаров группы С, ед.

Ограничения:

1. По использованию рабочего времени продавцов, чел-ч. 0,1х₁+0,2х₂+0,4х₃ 1100

2. По использованию площадей торговых залов, м² 0,05х₁+0,02х₂+0,02х₃ 120

3. По использованию площадей складских помещений, м² 3х₁+х₂+2х₃ 8000

4. Условие не отрицательности переменных х₁ 0, х₂ 0, х₃ 0.

Целевая функция:

Максимальное значение целевой функции, тыс. руб.

f(х) = 3х₁+5х₂+4х₃ mах

Алгоритм симплексного метода включает следующие этапы:

1.Составление первого опорного плана

Система ограничений задачи, решаемой симплексным методом задана в виде неравенств смысла “ ” , правые части которых в_i 0. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных х₄; х₅; х₆; которые образуют базис и называются базисными переменными и определяют объемы неиспользованных ресурсов:

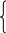0,1х₁+0,2х₂+0,4х₃ + х₄ = 1100

0,05х₁+0,02х₂+0,02х₃+х₅ = 120

3х₁+х₂+2х₃+х₆ = 8000

Матрица коэффициентов А=(а_ij) этой системы уравнений имеет вид:

А = 0,1	0,2	0,4	1	0	0
0,05	0,02	0,02	0	1	0
3	1	2	0	0	1

Решим систему уравнений относительно базисных переменных:

х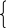 ₄ = 1100 – (0,1х₁+0,2х₂+0,4х₃)

х₅ = 120 – (0,05х₁+0,02х₂+0,02х₃)

х₆ = 8000 – (3х₁+х₂+3х₃)

Функцию цели запишем в виде уравнения f(х) = 0 – (-3х₁ – 5х₂ – 4х₃). Полагая что основные переменные х₁=0 х₂=0 х₃=0, получим первый опорный план, х₄=в₁; х₅=в₂; х₆=в₃ f(x) =0; который заносим в симплексную таблицу № 1. Она состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами функции цели, взятыми с противоположным знаком:

План	Базисные переменные	Свободные члены	Основн. перемен.			Допол.перем.			i
			х1	х2	х3	х6	х5	х6
I	х4	1100	0,1	0,2	0,4	1	0	0	5500
	х5	120	0,05	0,02	0,02	0	1	0	6000
	х6	8000	3	1	2	0	0	1	8000
Индексная строка	f(x)	0	-3	-5	-4	0	0	0