3.3 Частные случаи распространения плоских электромагнитных волн

Рассмотрим некоторые частные случаи сред, от электрофизических характеристик которых зависят особенности распространения ЭМВ.

Свободное пространство (вакуум). Это идеальная среда, для которой

, , .

Коэффициент распространения величина чисто мнимая и волна распространяется без затухания. Скорость распространения

Волны , т.е. равна скорости света и не зависит от частоты. Характеристическое сопротивление вакуума

- величина действительная, т.е. в любой точке z поля E и H находятся в фазе.

Диэлектрик с малыми потерями. Такие материалы широко используются в аппаратуре радиоэлектроники и связи, для них tg (δ) = 10^-3 – 10^-5 .

Коэффициент распространения

(3.14)

Так как tg (δ) << 1, можно приближенно вычислить корень квадратный в (3.14)

(3.15)

и тогда:

(3.16)

Для характеристического сопротивления, используя приближенное вычисление корня, легко получить

(3.17)

Комплексный характер Z_C показывает на небольшую несинфазность напряженностей полей E и H, которой на практике можно пренебречь.

Хорошо проводящая среда. Для металлоподобных сред , т.е. плотность токов проводимости значительно больше токов смещения. Комплексную диэлектрическую проницаемость можно считать чисто мнимой

Коэффициент распространения

(3.18)

Учитывая, что ,

из (3.18) получим . (3.19)

Аналогично найдем

. (3.20)

В хорошо проводящей среде сдвиг по фазе между E и H cоставляет 45⁰ и величина сопротивления зависит от частоты (явление дисперсии).

Амплитуда поля в металле изменяется по закону . Расстояние d, на котором амплитуда поля уменьшается в е = 2,718 раз называется толщиной скин-слоя ( глубиной проникновения )

(3.21)

Например, для меди ( σ = 5,7•10⁷ См/м) на частоте 1 ГГц. (λ = 30 см) глубина скин-слоя 6 мкм.

3.4 Падение плоской электромагнитной волны на границу раздела сред

Рассмотрим случай, когда плоская ЭМВ, распространяющаяся в среде 1, падает на границу раздела со средой 2, под некоторым углом падения  , который лежит в пределах 0⁰    90⁰. Геометрия задача и оси координат показаны на рис 3.4.

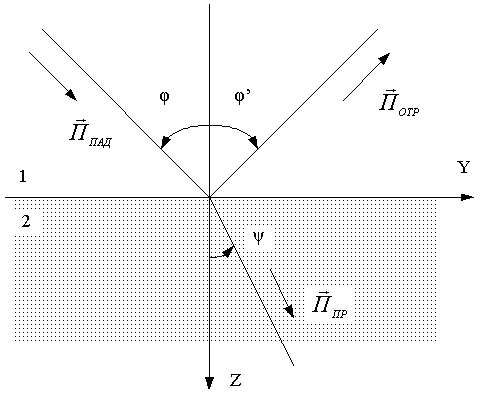
Риc. 3.4

Введем волны – падающую, отраженную и преломленную. Векторы Пойтинга всех перечисленных волн лежат в одной плоскости, называемой плоскостью падения.

Из курса физики известно, что между введенными углами существует определенная зависимость, а именно:

угол падения равен углу отражения, т.е.

(3.22)

и имеет место закон Снелля

(3.23)

где , - коэффициенты фазы плоских волн в средах 1 и 2 .

Формулу (3.23) можно переписать

(3.24)

где - показатель преломления физической среды.

Отмеченные выше закономерности справедливы при любой ориентации векторов электромагнитного поля. Представляют интерес два случая, которые рассматриваются ниже.

Перпендикулярная поляризация. В этом случае направление вектора Е перпендикулярно плоскости падения (рис. 3.5).

Пусть , и - комплексные амплитуды векторов напряженности электрического поля падающей, отраженной и преломленной волн. Граничные условия в плоскости z = 0 запишутся весьма просто:

(3.25)

При записи граничных условий для векторов напряженности магнитных полей следует учесть, что их касательная составляющая получается путем умножения модулей векторов Н на косинусы соответствующих углов.

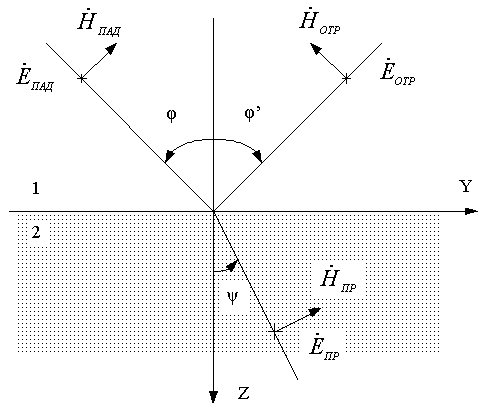
Рис. 3.5

Выразим векторы Н через вектор Е и соответствующие характеристические сопротивления сред. Таким образом, условие непрерывности касательных составляющих напряженности магнитного поля в плоскости z = 0 принимает вид:

(3.26)

Введем в рассмотрение коэффициент отражения R и коэффициент преломления Т по электрическому полю (нижний значок указывает, что эти величины относятся к случаю перпендикулярной поляризации):

, (3.27)

Теперь формулы (3.25) и (3.26) можно объединить, получив в результате систему двух линейных алгебраических уравнений относительно неизвестных R и Т :

,

(3.28)

Решение системы (3.28) имеет следующий вид:

(3.29)

(3.30)

Чтобы пользоваться формулами (3.29) и (3.30), необходимо, задавшись некоторым значением угла падения , предварительно вычислить угол преломления  на основания закона Снелля.

На практике часто приходится вычислять коэффициенты отражения и преломления плоских волн для частного случая, когда средой 1 служит вакуум или воздух ( = 1,  = 1), а средой 2 – немагнитный ( = 1) диэлектрик без потерь с относительной диэлектрической проницаемостью  . При этом формулы (3.29) и (3.30) удается объединить законом Снелля, записав их в следующем виде:

,

.

Параллельная поляризация. Этот случай характеризуется тем, что векторы Е всех трех волн – падающей, отраженной и преломленной – параллельны плоскости падения (рис.3.6)

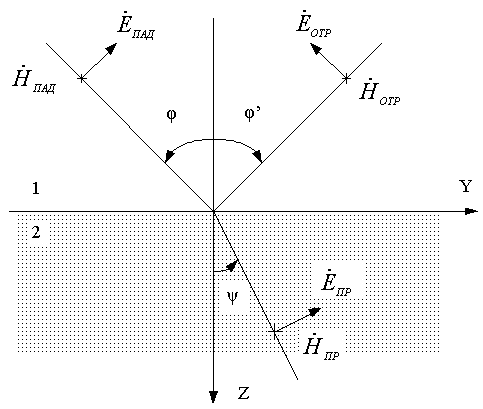
Рис. 3.6

По аналогии со случаем перпендикулярной поляризации запишем условия непрерывности тангенциальной составляющих векторов напряженности электрического и магнитного полей:

, (3.31)

(3.32)

Введем коэффициент отражения R_ и коэффициент преломления Т_ по электрическому полю (нижний значок указывает на то, что данные величины относятся к случаю параллельной поляризации). Разделив обе части равенств (3.31) и (3.32) на комплексную амплитуду Е_пад , получим следующую систему уравнений относительно неизвестных R и Т:

,

(3.33)

откуда

, (3.34)

. (3.35)

Если средой 2 служит немагнитный диэлектрик с относительной проницаемостью , формулы (3.34) и (3.35) приводятся к виду более удобному для инженерных расчетов.

(3.36)

(3.37)

При наклонном падении электромагнитной волны на границу раздела сред наблюдается два замечательных явления.

Углом Брюстера называется угол падения, при котором падающая волна полностью, без отражения, переходит через границу раздела двух материальных сред. Это явление наблюдается только для волн параллельной поляризации.

Условие R_|| = 0 ( см. ф-лу 3.34 ) приводит к уравнению

(3.38)

Если первая среда - вакуум, а вторая среда характеризуется относительной диэлектрической проницаемостью  , то из (3.36) имеем

откуда имеем

. (3.39)

Явление Брюстера используется в технике для создания устройств без отражений.

Явление полного внутреннего отражения наблюдается в случаях, когда среда 2 оптически менее плотная, чем среда 1 ( n₁  n₂ ). В этом случае  и имеется такое значение угла падения , когда преломленная волна будет распространяется параллельно границе раздела сред, т.е. под углом 90⁰. Данное критическое значение угла называется углом полного внутреннего отражения

(3.40)

При углах падения   _пво энергия падающей волны полностью отражается внутри среды с большей оптической плотностью. Явление полного внутреннего отражения используется в оптике, например, для изменения направления распространения пучка лучей при помощи призмы.