3. Плоские электромагнитные волны
3.1 Характеристики плоской скалярной волны
Волнами называются колебательные движения непрерывных сред. ЭМВ попадают под это определение. Для уяснения основных моментов колебаний рассмотрим простейший случай – однородную плоскую скалярную волну. Математически такая волна описывается формулой
(3.1)
Процесс изменяется в пространстве (z) и во времени (t), Vm - амплитуда волны, ω - круговая частота, β - коэффициент фазы.
Временная и пространственная
зависимость описывается гармонической
функцией. В точке z
= 0
.
В точке z > 0
,
т.е. колебания запаздывают на величину
βz . Уточним
временную зависимость колебаний. В
начальный момент времени (t
= 0)
.
Коэффициент фазы β
играет здесь роль пространственной
частоты. Размерность β
- рад./м., 1/м. Временной период волны
,
Пространственный период λ
- длина волны
.
На рис. 3.1 показано пространственное изменение поля для двух моментов времени.
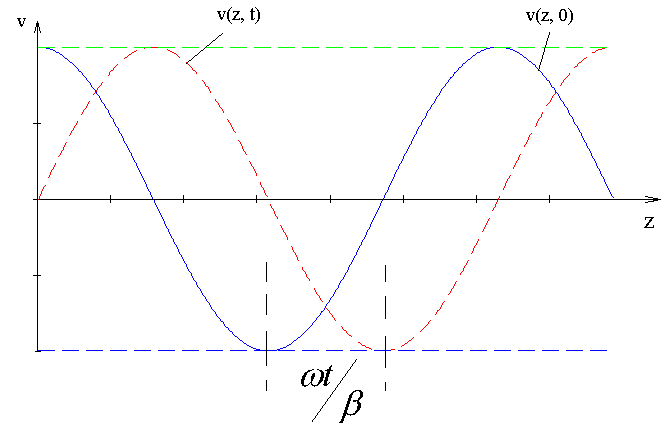
Рис. 3.1
Рассматриваемая волна называется плоской, это значит, что в любой плоскости, перпендикулярной оси 0Z, волна имеет одинаковую фазу. Эта плоскость называется фронтом волны. Уравнение фронта волны
Скорость перемещения фронта волны называется фазовой скоростью
(3.2)
Волна, распространяющаяся в направлении убывания координаты z, записывается аналогично (3.1)
(3.3)
и имеет такую же скорость распространения, как и прямая.
Реальные среды обладают потерями, что приводит к затуханию волны в процессе распространения. Закон изменения амплитуды волны можно записать так
,
где α - коэффициент затухания ( ослабления ) плоской волны с размерностью 1/м.
В расчетах также пользуются логарифмической единицей – погонным затуханием
.
(3.4)
Пространственная структура затухающей волны представлена на рис.3.2.
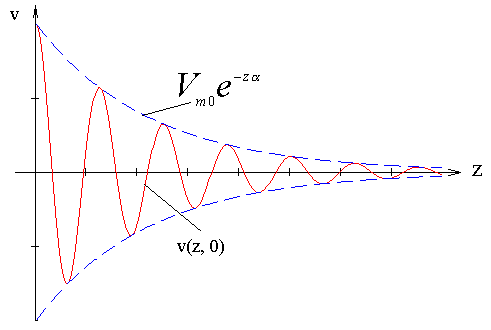
Рис. 3.2
Коэффициент фазы β и коэффициент затухания α являются показателями экспоненты и могут быть объединены в единую комплексную величину, которая зазывается коэффициентом распространения
(3.5)
В среде без потерь коэффициент
распространения величина чисто мнимая
.
3.2 Плоская электромагнитная волна
Электромагнитная волна (ЭМВ) - это
колебания векторов поля
и
,
распространяющихся в среде с заданными
электрофизическими параметрами
,
.
Ориентация вектора
в пространстве определяет плоскость
поляризации ЭМВ.
Плоская ЭМВ удовлетворяет двум исходным требованиям:
1. Составляющая
,
с другой стороны
;
2.
зависит только от координаты, вдоль
возрастания которой распространяется
волна (для определенности это координата
z) и, следовательно,
.
Из второго уравнения Максвелла для комплексных амплитуд (2.14) с учетом отмеченных выше положений пунктов 1 и 2 получим:
,
(3.6)
Подставляя
в первое уравнение (2.14) и выполняя
дифференцирование, получим дифференциальное
уравнение второго порядка для
,
(3.7)
где
. (3.8)
Общее решение уравнения
(3.7) представляет собой сумму экспонент
, (3.9)
где γ1, γ2 - корни уравнения (3.8).
На рис. 3.3 показано расположение γ2, γ1 и γ2 на комплексной плоскости.
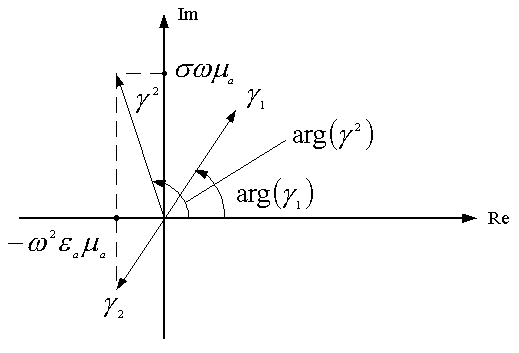
Рис. 3.3
Корень
лежит в первом квадранте и γ2
= - γ1. Формулу (3.9) перепишем
следующим образом
(3.10)
и отметим, что (3.10) является решением уравнения (3.7), которое называется уравнением Гельмгольца.
Вернувшись теперь к (3.6) , запишем для составляющей напряженности магнитного поля волны, бегущей в сторону
(3.11)
Из (3.11) видно, что и связаны в любой точке коэффициентом пропорциональности, который имеет размерность Ом называется характеристическим ( волновым ) сопротивлением волны т.е.
. (3.12)
Плотность потока мощности, переносимой плоской ЭМВ, равна среднему значению модуля вектора Пойтинга
(3.13)
В заключение отметим основные особенности плоской ЭМВ:
1. Векторы поля и перпендикулярны между собой.
2. В каждой точке пространства комплексные амплитуды напряженностей электрического и магнитного полей связаны между собой коэффициентом пропорциональности – характеристическим сопротивлением.
3. Ориентация вектора
показывает направление распространения
волны и направление переноса мощности.
4. Векторы , , образуют правую тройку векторов и подчиняются правилу буравчика.