6.3 Метод параллельного шлейфа

Шлейфом называется вспомогательная линия, включенная параллельно в линию с нагрузкой. При согласовании этим методом расчеты ведутся с использованием понятий проводимостей. Схема согласования приведена на рис. 6.3.

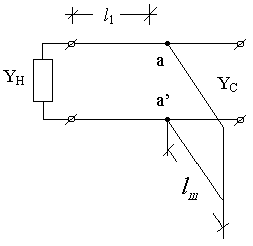
Рис. 6.3

Согласование производится в два этапа.

На первом этапе выбирается такое расстояние l₁ (см. рис. 6.3), чтобы в точках aa’ активная нормированная проводимость линии равнялась единице: . На рис. 6.4 показано расстояние

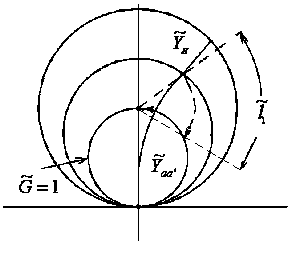
Рис. 6.4

На втором этапе выбирается такая длина параллельного шлейфа (l_Ш) к.з. или х.х., чтобы входная проводимость шлейфа была равна по величине и противоположна по знаку проводимости линии в точке включения шлейфа . Суммарная проводимость в точках aa’ будет:

. (6.2)

Траектория рабочей точки на круговой диаграмме при согласовании показана на рис. 6.4 стрелками.

Метод параллельного шлейфа используется для согласования нагрузок в коаксиальных, двухпроводных и волноводных ЛП. В первых двух типах линий, шлейфы выполняются в виде таких же линий как основная линия с нагрузкой. По конструктивным соображениям шлейф к.з. предпочтительнее шлейфам х.х.

В линиях из прямоугольных волноводов параллельные реактивные проводимости реализуются в виде тонких металлических перегородок – диафрагм. На рис. 6.5 показаны два типа диафрагм: индуктивная и емкостная.

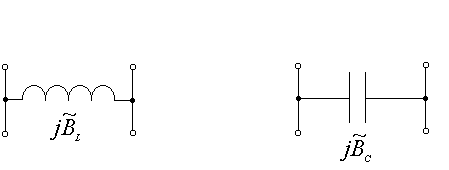
Рис. 6.5

Значения проводимостей рассчитываются по формулам:

,

(6.3)

,

В (6.3) формулы определены для волны основного типа прямоугольного волновода – H₁₀, λ_В - длина волны в волноводе.

7. Матричное описание многополюсников сверхвысоких частот

7.1 Многополюсники сверхвысоких частот

В технике СВЧ 2N-полюсником называется комбинация проводников, полупроводников и диэлектриков, имеющая N доступных входов в виде отрезков линий с заданными характеристиками. На эквивалентной схеме входы представляются в виде двухпроводных линий (по два полюса), на которых задаются сечения (плоскости отсчета), для которых фиксируются амплитуды и фазы напряжений и токов. Самым распространенным типом является четырехполюсник (рис. 7.1).

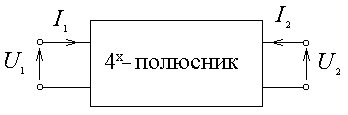
Рис. 7.1

Связь между U и I на входах четырехполюсника можно установить или с помощью уравнений Кирхгофа, или с помощью таблицы коэффициентов, которая называется матрицей. Если матрицы устанавливает связь между U и I, то такие матрицы называются классическими. Если матрица устанавливает связь между напряжением падающих и отраженных волн, то они называются волновыми.

В общем случае матрица 2N-полюсника содержит N² независимых коэффициентов. Симметричные устройства описываются меньшим количеством элементов матрицы. Плоскости симметрии могут проходить между входами устройства или между клеммами.

7.2 Матрицы 4х-полюсника и их свойства

Соотношения между напряжениями и токами на входах 4х-полюсника (рис. 7.1) можно записать в виде системы уравнений Кирхгофа:

,

(7.1)

.

Эту систему можно переписать в виде матричного уравнения

, (7.2)

где [U], [I] - матрицы – столбцы, а [Z] - квадратная матрица

. (7.3)

Перемножая в правой части (7.2) матрицы [Z] на [I] по правилу «строка на столбец», мы снова придем к записи (7.1).

Для 4х-полюсника рис. 7.1 можно установить связь токов и напряжений и прийти к эквивалентному матричному уравнению:

, (7.4)

где [Y] - квадратная матрица проводимостей.

Физический смысл элементов матриц [Z] и [Y] можно установить, выполняя режимы х.х и к.з. на входах 4х-полюсника. Так, разорвав цепь на выходе два (I₂ = 0), можно установить из (7.1), что Z₁₁ – это входное сопротивление 4х-полюсника с первого входа, Z₂₁ – это взаимное сопротивление.

Еще одна матрица - [A] устанавливает связь между напряжением и током на входе и на выходе 4х-полюсника:

. (7.5)

Следует заметить, что матрица [A], записывается для случая, когда ток I₂ направлен в противоположную сторону току I₂ на рис. 7.1.

Матрицы [Z], [Y], [A] являются классическими и описывают свойства одного и того же 4х-полюсника. Следовательно, элементы одной матрицы могут быть выражены через элементы второй и третьей. Преимущества использования конкретной матрицы проявляется при анализе составных 4x-полюсников. Так при последовательном включении исходных 4х-полюсников, матрица [Z] составного 4х-полюсника равна сумме матриц исходных 4х-полюсников, при параллельном включении - сумме матриц проводимостей. При каскадном включении исходных 4х-полюсников матрица [А] составного 4х-полюсника равна произведению соответствующих матриц исходных 4х-полюсников.

Как отмечалось в главе 3, не для всех типов линий можно однозначно определить напряжение и ток. В этих условиях о свойствах 4х-полюсника можно судить по соотношению напряжений падающих и отраженных волн на входах (рис. 7.2).

Рис. 7.2

Соответствующая система уравнений имеет вид:

,

. (7.6)

Или в матричном виде

, (7.7)

где [S] - матрица рассеяния.

Физический смысл элементов матрицы [S] выявляется при подключении согласованных нагрузок на входах 4-х полюсника. Так, если U_{2 ПАД} = 0, то из уравнения (7.6) следует, что - коэффициент отражения от первого входа, - коэффициент передачи с первого входа на второй.

Отметим некоторые свойства 4х-полюсников, вытекающие из свойств матриц.

а) Свойство взаимности. Если Y₂₁ = Y₂₁ (или Z₂₁ = Z₂₁), то 4х-полюсник называется взаимным.

б) Свойство симметрии. Если Z₁₁ = Z₂₂ или Y₁₁ = Y₂₂, то 4х-полюсник называется симметричным.

в) Свойство реактивности. Если все элементы матрицы [Z] чисто мнимые, например, Z₁₁ = jX₁₁ (или Y₁₁ = jB₁₁), то 4х-полюсник называется реактивным.

В реактивном 4х-полюснике нет омических потерь. Матрица рассеяния такого устройства удовлетворяет условию унитарности

, (7.8)

где - матрица транспонированная, комплексно-сопряженная исходной; [E] - единичная матрица.

Условие (7.8) справедливо для любого многополюсника без потерь.

Описанные и отмеченные свойства 4х-полюсников и их матрицы могут быть обобщены на случай многополюсников.