5. Основы теории цепей с распределенными параметрами
5.1. Цепи с сосредоточенными элементами и с распределенными параметрами
На низких и умеренно высоких частотах (до сотен МГц) электронные функциональные схемы выполнены с использованием сосредоточенных элементов: резисторов, конденсаторов, катушек индуктивности. Место их положения в схеме локализовано. Такие схемы-цепи называются схемами с сосредоточенными элементами. При переходе к СВЧ размеры элементов уменьшаются, добротность колебательных систем падает, в основном, за счет увеличения омического сопротивления токоведущих частей схемы и за счет эффектов ЭМ излучения элементов. Основной путь построения колебательных систем СВЧ заключается в использовании в качестве элементов отрезков ЛП или, как говорят, цепей с распределенными параметрами. Отрезок ЛП с малыми потерями характеризуются удельными (приходящимися на единицу длины линии) индуктивностью – L’ Гн/м и емкостью – C’ Ф/м. Основные характеристики линии могут быть выражены через эти параметры:
,
.
Тем самым устанавливается эквивалентность между волновым описанием процессов в линии и решением на основе эквивалентного представления линии в виде каскадно-включенных звеньев из погонных параметров.
5.2. Решение телеграфных уравнений. Падающие и отраженные волны
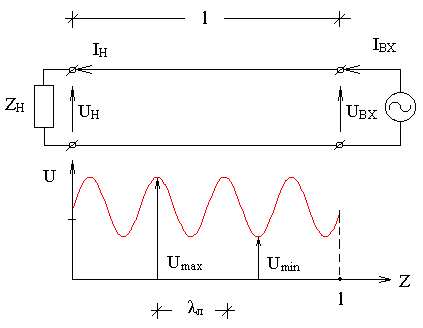
Распространенная схема техники СВЧ приведена на рис. 5.1: нагрузка, характеризуемая комплексным сопротивлением ZH, подключенная к генератору через отрезок линии длиной l c заданными характеристиками β, ZC, α.
Zc
z
Рис. 5.1
Распределение реальных или эквивалентных токов и напряжений вдоль ЛП зависит от соотношения параметров линии и нагрузки. Эти распределения описываются, так называемыми, телеграфными уравнениями. Решение телеграфных уравнений для линии без потерь (α → 0) имеет следующий вид:
,
(5.1)
.
Распределение U и I вдоль линии носит периодический характер с периодом равным длине волны в линии - λЛ.
Из уравнений (5.1) можно определить входное сопротивление нагруженной линии, положив z = l:
(5.2)
Физически неравномерный характер распределение тока и напряжения вдоль нагруженной линии объясняется наличием двух волн: прямой (падающей), распространяющейся от генератора к нагрузке, и обратной (отраженной), распространяющейся в обратном направлении. Взаимодействие (интерференция) этих волн приводит к образованию пучностей (максимумов) и узлов (минимумов). В первом случае волны складываются в фазе, во втором – в противофазе.
Заменяя в первом уравнении (5.1) cos(βz) и sin(βz) по формулам Эйлера через экспоненты, можно объединить слагаемые, содержащие в качестве множителя e+jβz - это подающая волна с амплитудой U+ , второе слагаемое с e-jβz - это отраженная волна с амплитудой U- .
Для установления соотношения между этими волнами вводится коэффициент отражения, модуль которого
(5.3)
меняется в интервале от 0 до 1.
В максимумах волны складываются в фазе
,
в минимумах – в противофазе:
.
Параллельно с Г вводится еще один
параметр – коэффициент стоячей волны:
. (5.4)
Пределы изменения коэффициента: 1 ≤ КСВ ≤ ∞. Иногда пользуются обратной величиной – коэффициентом бегущей волны - КБВ =1⁄КСВ. КСВ используется на практике для определения режима работы нагруженной линии с использованием измерительной линии, способной с помощью перемещающегося зонда регистрировать UMAX и UMIN. Коэффициент отражения определяется расчетным путем, в соответствии с формулой (5.4)
Если нагрузка является чисто активной (ZH = RH), то КСВ может быть определен расчетным путем:
,
;
(5.5)
,
.
При произвольном соотношении падающей и отраженной волн в линии устанавливается режим смешенных волн. Если отражений нет (Г = 0), в линии устанавливается режим бегущей волны – распределение напряжения и тока вдоль линии равномерное. В случае, если амплитуда отраженной волны равна амплитуде падающей (|Г| = 1), в линии устанавливается режим стоячих волн – синусоидальное или косинусоидальное распределение модуля напряжения и тока.
Выше было отмечено, что решение телеграфных уравнений (5.1) записываются для реальных или эквивалентных напряжений и токов. Для всех типов колебаний, кроме Т, U и I - эквивалентные значения определяются в соответствии с законом Ома по значению мощности, переносимой рассматриваемой волной.