
- •Министерство образования и науки российской федерации
- •Содержание:
- •Кинематика поступательного и вращательного движения
- •Динамика поступательного и вращательного движения.
- •Работа. Энергия
- •Законы сохранения в механике
- •Элементы специальной теории относительности
- •Средняя энергия молекул
- •Распределения Максвелла и Больцмана
- •Первое начало термодинамики
- •Второе начало термодинамики. Энтропия.
- •Электростатическое поле в вакууме
- •Законы постоянного тока
- •Магнитостатика
- •Явление электромагнитной индукции
- •Электрические и магнитные свойства вещества
- •Свободные и вынужденные колебания
- •Сложение гармонических колебаний
- •Волны. Уравнение волны
- •Энергия волны. Перенос энергии волной
- •Уравнения Максвелла
- •Интерференция и дифракция света
- •Поляризация и дисперсия света
- •Тепловое излучение. Фотоэффект
- •Эффект Комптона. Световое давление
- •Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Спектр атома водорода. Правило отбора
- •Уравнение Шредингера
- •Ядерные реакции
- •Ядро. Элементарные частицы
- •Фундаментальные взаимодействия.
Средняя энергия молекул
№1
Средняя
кинетическая энергия молекул газа при
температуре
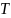 зависит от их конфигурации и структуры,
что связано с возможностью различных
видов движения атомов в молекуле и самой
молекулы. При условии, что имеет место
только поступательное и вращательное
движение молекулы как целого, средняя
кинетическая энергия молекул азота
зависит от их конфигурации и структуры,
что связано с возможностью различных
видов движения атомов в молекуле и самой
молекулы. При условии, что имеет место
только поступательное и вращательное
движение молекулы как целого, средняя
кинетическая энергия молекул азота
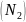 равна …
равна …
Решение:
Для
статической системы в состоянии
термодинамического равновесия на каждую
поступательную и вращательную степени
свободы приходится в среднем кинетическая
энергия, равная
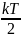 , а на каждую колебательную степень –
, а на каждую колебательную степень –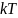 .
Средняя кинетическая энергия молекулы
равна
.
Средняя кинетическая энергия молекулы
равна
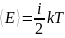 ; где
; где
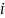 –сумма числа поступательных, числа
вращательных и удвоенного числа
колебательных степеней свободы молекулы.
При условии, что имеют место только
поступательное и вращательное движение,
сумма числа степеней с
–сумма числа поступательных, числа
вращательных и удвоенного числа
колебательных степеней свободы молекулы.
При условии, что имеют место только
поступательное и вращательное движение,
сумма числа степеней с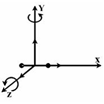 вободы
равна
вободы
равна
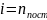 +
+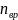 -число степеней свободы поступательного
движения, равное
-число степеней свободы поступательного
движения, равное
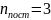 ;
–число
степеней свободы вращательного движения,
которое может быть равно
;
–число
степеней свободы вращательного движения,
которое может быть равно
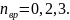 Для молекулярного азота (двухатомной
молекулы)
Для молекулярного азота (двухатомной
молекулы)
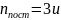
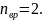 Следовательно,
Следовательно,
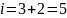 (3 степени свободы поступательного
движения по направлениям осей ординат
(3 степени свободы поступательного
движения по направлениям осей ординат
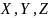 и
2 степени свободы вращательного движения
вокруг осей
и
2 степени свободы вращательного движения
вокруг осей
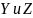 )
(см. рис.) Тогда средняя энергия молекул
азота
равна
)
(см. рис.) Тогда средняя энергия молекул
азота
равна
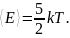
№2
В соответствии с законом равномерного
распределения энергии по степеням
свободы средняя кинетическая энергия
молекулы идеального газа при температуре
T
равна:
.
Здесь
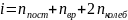 ,
где
,
где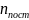 ,
и
,
и –
число степеней свободы поступательного,
вращательного и колебательного движений
молекулы соответственно. Для гелия (He)
число i
равно …
–
число степеней свободы поступательного,
вращательного и колебательного движений
молекулы соответственно. Для гелия (He)
число i
равно …
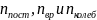 3
3
№3
В соответствии с законом равномерного
распределения энергии по степеням
свободы средняя кинетическая энергия
молекулы идеального газа при температуре
T
равна:
.
Здесь
,
где
,
и
–
число степеней свободы поступательного,
вращательного и колебательного движений
молекулы соответственно. Для
азота
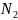 средняя кинетическая энергия
колебательного движения молекулы
равна …
средняя кинетическая энергия
колебательного движения молекулы
равна …
Ответ:
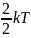
№4 Средняя кинетическая энергия молекулы идеального газа при температуре T равна . Здесь , При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно …
Ответ:6
№5
Средняя
кинетическая энергия молекул газа при
температуре
![]() зависит
от их конфигурации и структуры, что
связано с возможностью различных видов
движения атомов в молекуле и самой
молекулы. При условии, что имеет место
поступательное, вращательное движение
молекулы как целого и колебательное
движение атомов в молекуле, средняя
кинетическая энергия молекулы кислорода
(
зависит
от их конфигурации и структуры, что
связано с возможностью различных видов
движения атомов в молекуле и самой
молекулы. При условии, что имеет место
поступательное, вращательное движение
молекулы как целого и колебательное
движение атомов в молекуле, средняя
кинетическая энергия молекулы кислорода
(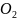 )
равна …
)
равна …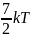
№6 Если не учитывать колебательные движения в молекуле водяного пара, то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно …1/2
№7
При
комнатной температуре отношение
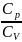 молярных теплоемкостей при постоянном
давлении и постоянном объеме равно
молярных теплоемкостей при постоянном
давлении и постоянном объеме равно
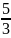 для …
для …
Решение
Из
отношения
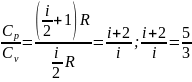 найдем
найдем
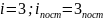 ,
. Только 3 поступательные степени свободы
имеют одноатомные газы, следовательно,
это гелий.
,
. Только 3 поступательные степени свободы
имеют одноатомные газы, следовательно,
это гелий.
№8
На каждую степень свободы движения
молекулы проходится одинаковая энергия,
равная
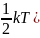 постоянная Больцмана,
постоянная Больцмана,
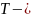 температура по шкале Кельвина). Средняя
кинетическая энергия атомного водорода
равна …
температура по шкале Кельвина). Средняя
кинетическая энергия атомного водорода
равна …
Решение
Средняя кинетическая энергия молекул
равна
, где
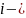 число степеней свободы молекулы.
Атомарный водород –это одноатомный
газ, атомы которого в данной модели
участвуют только в поступательном
движении
число степеней свободы молекулы.
Атомарный водород –это одноатомный
газ, атомы которого в данной модели
участвуют только в поступательном
движении
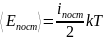 .
Число степеней свободы
.
Число степеней свободы
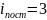 , т.к. положение центра инерции атома
задается тремя координатами
, т.к. положение центра инерции атома
задается тремя координатами
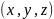 .
Следовательно,
.
Следовательно,
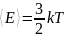 .
.
