
- •Министерство образования и науки российской федерации
- •Содержание:
- •Кинематика поступательного и вращательного движения
- •Динамика поступательного и вращательного движения.
- •Работа. Энергия
- •Законы сохранения в механике
- •Элементы специальной теории относительности
- •Средняя энергия молекул
- •Распределения Максвелла и Больцмана
- •Первое начало термодинамики
- •Второе начало термодинамики. Энтропия.
- •Электростатическое поле в вакууме
- •Законы постоянного тока
- •Магнитостатика
- •Явление электромагнитной индукции
- •Электрические и магнитные свойства вещества
- •Свободные и вынужденные колебания
- •Сложение гармонических колебаний
- •Волны. Уравнение волны
- •Энергия волны. Перенос энергии волной
- •Уравнения Максвелла
- •Интерференция и дифракция света
- •Поляризация и дисперсия света
- •Тепловое излучение. Фотоэффект
- •Эффект Комптона. Световое давление
- •Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Спектр атома водорода. Правило отбора
- •Уравнение Шредингера
- •Ядерные реакции
- •Ядро. Элементарные частицы
- •Фундаментальные взаимодействия.
Законы сохранения в механике
№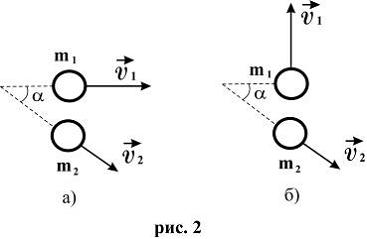 1
Шар
массы
,
движущийся со скоростью
1
Шар
массы
,
движущийся со скоростью
 ,
налетает на покоящийся шар массы
,
налетает на покоящийся шар массы
 (рис. 1). Могут ли после соударения скорости
шаров,
(рис. 1). Могут ли после соударения скорости
шаров, и
и
 ,
иметь направления, показанные на рис.
2 (а
и б).
,
иметь направления, показанные на рис.
2 (а
и б).
Ответ: могут в случае б
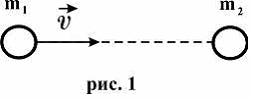
№2
Шар массой
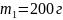 ,
движущийся со скоростью
,
движущийся со скоростью
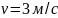 ,
налетает на покоящийся шар массой
,
налетает на покоящийся шар массой
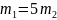 (см.
рис.1). Если удар абсолютно неупругий,
скорость шаров (в м/с)
после удара равна
(см.
рис.1). Если удар абсолютно неупругий,
скорость шаров (в м/с)
после удара равна
Ответ: 0,5
№3
Диск и обруч, имеющие одинаковые массы
и радиусы, вкатываются без проскальзывания
с одинаковыми скоростями на горку. Если
трением и сопротивлением воздуха можно
пренебречь, то отношение высот
 ,,
на которые смогут подняться эти тела,
равно …
,,
на которые смогут подняться эти тела,
равно …
Ответ: ¾.
№4 График зависимости кинетической энергии тела, брошенного с поверхности земли под некоторым углом к горизонту, от высоты подъема имеет вид, показанный на рисунке …
Р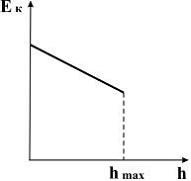 ешение:
Из
закона сохранения механической энергии
ешение:
Из
закона сохранения механической энергии
 .
Отсюда
.
Отсюда
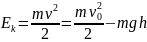 ,
то есть зависимость Ek
(h) –
линейная, причем, если h
=0,
,
то есть зависимость Ek
(h) –
линейная, причем, если h
=0,
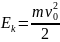
 ;
если же h=hmax
,
;
если же h=hmax
, . Поэтому график зависимости кинетической
энергии от высоты подъема тела, брошенного
с поверхности земли под некоторым углом
. Поэтому график зависимости кинетической
энергии от высоты подъема тела, брошенного
с поверхности земли под некоторым углом
![]() к
горизонту, имеет вид.
к
горизонту, имеет вид.
№5
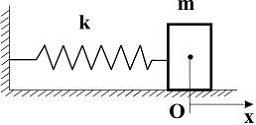
Тело массы m, прикрепленное к пружине с жесткостью k, может без трения двигаться по горизонтальной поверхности (пружинный маятник). График зависимости кинетической энергии тела от величины его смещения из положения равновесия имеет вид, показанный на рисунке …
Р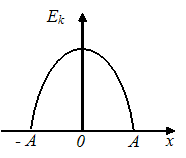 ешение:
По
условию задачи трение отсутствует.
Следовательно, в системе выполняется
закон сохранения механической энергии:
ешение:
По
условию задачи трение отсутствует.
Следовательно, в системе выполняется
закон сохранения механической энергии: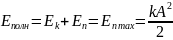 , где А
–
амплитуда колебаний. Отсюда
, где А
–
амплитуда колебаний. Отсюда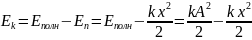 .
Это уравнение параболы со смещенной
вершиной; ветви параболы направлены
вниз. Поэтому график зависимости
кинетической энергии тела от величины
его смещения из положения равновесия
имеет вид.
.
Это уравнение параболы со смещенной
вершиной; ветви параболы направлены
вниз. Поэтому график зависимости
кинетической энергии тела от величины
его смещения из положения равновесия
имеет вид.
№ 6
Тело
массой m,
прикрепленное к пружине жесткостью k,
может без трения двигаться по горизонтальной
поверхности (пружинный маятник). Если
А – амплитуда колебаний, то при смещении
тела из положения равновесия на величину
6
Тело
массой m,
прикрепленное к пружине жесткостью k,
может без трения двигаться по горизонтальной
поверхности (пружинный маятник). Если
А – амплитуда колебаний, то при смещении
тела из положения равновесия на величину
 скорость
тела составит…
скорость
тела составит…
Решение:
По
условию задачи трение отсутствует.
Следовательно, в системе выполняется
закон сохранения механической энергии:
, где А
–
амплитуда колебаний. Отсюда
 .
C
другой стороны
.
C
другой стороны
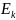
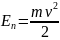 ,
отсюда
,
отсюда
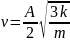 .
.
№7 Фигурист вращается вокруг вертикальной оси с определенной частотой. Если он прижмет руки к груди, уменьшив тем самым свой момент инерции относительно оси вращения в 2 раза, то …
Решение:
Согласно
закону сохранения момента импульса
 .
Здесь J – момент инерции фигуриста
относительно оси вращения, ω – угловая
скорость его вращения вокруг этой оси.
Отсюда с учетом того, что ω=2πn
, где n
– частота вращения,
.
Здесь J – момент инерции фигуриста
относительно оси вращения, ω – угловая
скорость его вращения вокруг этой оси.
Отсюда с учетом того, что ω=2πn
, где n
– частота вращения,
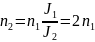 .
Кинетическая энергия тела, вращающегося
вокруг неподвижной оси, равна:
.
Кинетическая энергия тела, вращающегося
вокруг неподвижной оси, равна:
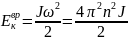 .
Тогда
.
Тогда
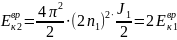 .
Таким образом, частота вращения фигуриста
и его кинетическая энергия возрастут
в 2 раза.
.
Таким образом, частота вращения фигуриста
и его кинетическая энергия возрастут
в 2 раза.
№8 Шар и полная сфера, имеющие одинаковые массы и радиусы, вкладываются без проскальзывания на горку. Если начальные скорости этих тел одинаковы, то …
Р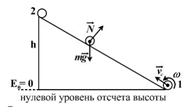 ешение:
Воспользуемся
законом сохранения механической энергии.
Полная энергия тел не изменяется, поэтому
ешение:
Воспользуемся
законом сохранения механической энергии.
Полная энергия тел не изменяется, поэтому
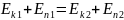 . Кинетическая энергия плоского движения
твердого тела равна сумме кинетической
энергии поступательного движения и
кинетической энергии вращения вокруг
оси, проходящей через центр масс:
. Кинетическая энергия плоского движения
твердого тела равна сумме кинетической
энергии поступательного движения и
кинетической энергии вращения вокруг
оси, проходящей через центр масс:
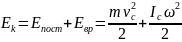 .
В последней формуле
.
В последней формуле
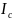 -
момент инерции тела относительно оси,
В
последней формуле
– момент инерции тела относительно
оси, проходящий через его центр масс ;
-
момент инерции тела относительно оси,
В
последней формуле
– момент инерции тела относительно
оси, проходящий через его центр масс ;
 –скорость его центра масс. Из условия
отсутствия проскальзывания следует,
что мгновенные скорости точек касания
тела о горку равны нулю, то есть угловая
скорость
–скорость его центра масс. Из условия
отсутствия проскальзывания следует,
что мгновенные скорости точек касания
тела о горку равны нулю, то есть угловая
скорость
 .
В нашем случае, энергии тела в первом
и во втором состояниях равны:
.
В нашем случае, энергии тела в первом
и во втором состояниях равны:
 ,
,

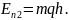 Из закона сохранения энергии
Из закона сохранения энергии
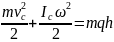 следует
следует
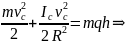
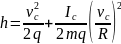 .
Анализируя последнюю формулу, видим,
что при равенстве масс, скоростей
радиусов однородного шара и полой сферы
.
Анализируя последнюю формулу, видим,
что при равенстве масс, скоростей
радиусов однородного шара и полой сферы
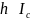 . Сравним моменты инерции тел, обозначив
их у шара
. Сравним моменты инерции тел, обозначив
их у шара
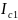 ,
у полой сферы -
,
у полой сферы - .
Момент инерции
.
Момент инерции
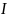 –величина, характеризующая распределение
массы тела относительно оси вращения
и являющаяся мерой инертности тела при
вращательном движении. Вся масса полой
сферы находится на расстоянии
–величина, характеризующая распределение
массы тела относительно оси вращения
и являющаяся мерой инертности тела при
вращательном движении. Вся масса полой
сферы находится на расстоянии
 от оси вращения, а у шара распределена
равномерно вдоль радиуса сферы. Тогда
от оси вращения, а у шара распределена
равномерно вдоль радиуса сферы. Тогда
 ,
следовательно,
,
следовательно,
 . Значит, полая сфера поднимается на
горку выше, чем однородный шар.
. Значит, полая сфера поднимается на
горку выше, чем однородный шар.
№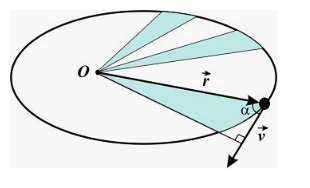 9
В случае
действия на тело центральной силы
радиус-вектор, проведенный к нему из
центра, описывает в равные промежутки
времени равные площади. (В этом, собственно,
и состоит по отношению к движению планет
второй закон Кеплера.) Если в начальный
момент расстояние от планеты до Солнца
r
, скорость v,
угол между скоростью планеты и
радиус-вектором r
равен α,
то за время t
радиус-вектор, проведенный от Солнца к
планете, опишет площадь…
9
В случае
действия на тело центральной силы
радиус-вектор, проведенный к нему из
центра, описывает в равные промежутки
времени равные площади. (В этом, собственно,
и состоит по отношению к движению планет
второй закон Кеплера.) Если в начальный
момент расстояние от планеты до Солнца
r
, скорость v,
угол между скоростью планеты и
радиус-вектором r
равен α,
то за время t
радиус-вектор, проведенный от Солнца к
планете, опишет площадь…
Р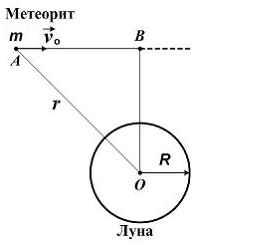 ешение:
Закон
равных площадей или 2-й закон Кеплера
является следствием закона сохранения
момента импульса для движения в
центральном поле. Выразим момент импульса
тела через заданные параметры начального
положения: . Из закона сохранения момента
импульса следует, что величина
ешение:
Закон
равных площадей или 2-й закон Кеплера
является следствием закона сохранения
момента импульса для движения в
центральном поле. Выразим момент импульса
тела через заданные параметры начального
положения: . Из закона сохранения момента
импульса следует, что величина
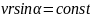 ,
т.е. должна оставаться постоянной в
процессе движения. Площадь, описываемая
радиус-вектором за бесконечно малый
промежуток времени будет равна площади
треугольника с гипотенузой r,
катетами
,
т.е. должна оставаться постоянной в
процессе движения. Площадь, описываемая
радиус-вектором за бесконечно малый
промежуток времени будет равна площади
треугольника с гипотенузой r,
катетами
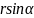 и
и
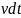 ,
то есть
,
то есть
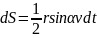 .
Следовательно, за время t
радиус-вектор, проведенный от Солнца к
планете, опишет площадь
.
Следовательно, за время t
радиус-вектор, проведенный от Солнца к
планете, опишет площадь
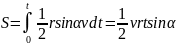 .
.
№10
Находясь
на расстоянии
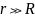 по направлению к Луне летит метеорит,
скорость которого
.
Для расчета минимального прицельного
расстояния OB,
при котором метеорит не упадет на
поверхность Луны, используют законы
сохранения механической энергии и
момента импульса.Выберите из предложенных
вариантов верную запись этих законов.
Радиус R
и массу M
планеты Луна, гравитационную постоянную
G
,скорость метеорита вблизи поверхности
Луны считать известными.
по направлению к Луне летит метеорит,
скорость которого
.
Для расчета минимального прицельного
расстояния OB,
при котором метеорит не упадет на
поверхность Луны, используют законы
сохранения механической энергии и
момента импульса.Выберите из предложенных
вариантов верную запись этих законов.
Радиус R
и массу M
планеты Луна, гравитационную постоянную
G
,скорость метеорита вблизи поверхности
Луны считать известными.
Р ешение:
Метеорит
массой m
должен двигаться по гиперболической
орбите,касающейся поверхности Луны в
точке C.
При движении по этой траектории
выполняется закон сохранения механической
энергии:
ешение:
Метеорит
массой m
должен двигаться по гиперболической
орбите,касающейся поверхности Луны в
точке C.
При движении по этой траектории
выполняется закон сохранения механической
энергии:
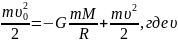 -скорость
метеорита вблизи Луны. Действительно,
метеорит приближается к Луне под
действием силы тяготения.работа этой
силы является мерой увеличения
кинетической энергии метеорита и
одновременно мерой уменьшения его
потенциальной энергии от 0 в точке А до
-скорость
метеорита вблизи Луны. Действительно,
метеорит приближается к Луне под
действием силы тяготения.работа этой
силы является мерой увеличения
кинетической энергии метеорита и
одновременно мерой уменьшения его
потенциальной энергии от 0 в точке А до
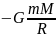 в точке С. Луна из-за большой массы в
процессе взаимодействия будет оставаться
в покое, а вследствие равенства нулю
момента силы притяжения относительно
центра Луны момент импульса метеорита
относительно центра Луны будет
сохраняться. Итак, для расчета мимнимального
прицельного расстояния используется
сситема уравнений
в точке С. Луна из-за большой массы в
процессе взаимодействия будет оставаться
в покое, а вследствие равенства нулю
момента силы притяжения относительно
центра Луны момент импульса метеорита
относительно центра Луны будет
сохраняться. Итак, для расчета мимнимального
прицельного расстояния используется
сситема уравнений
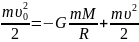 ,
m
,
m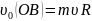 .
.
№11
Диск
в одном случае скатывается без
проскальзывания с наклонной плоскости
высотой
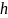 ,
а в другом случае соскальзывает с нее.
Если трением можно пренебречь, то
отношение скоростей диска
,
а в другом случае соскальзывает с нее.
Если трением можно пренебречь, то
отношение скоростей диска
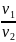 у
основания наклонной плоскости будет
равно …
у
основания наклонной плоскости будет
равно …
Решение: В рассматриваемой системе «тело – Земля» действуют только консервативные силы, поэтому в ней выполняется закон сохранения механической энергии, применяя который можно найти искомую скорость диска в обоих случаях:
 и
и
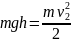 .
С учетом того, что момент инерции диска
относительно оси вращения
и
.
С учетом того, что момент инерции диска
относительно оси вращения
и
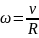 , получаем из первого уравнения
, получаем из первого уравнения
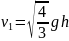 , а из второго уравнения –
, а из второго уравнения –
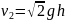 . Тогда искомое отношение равно
. Тогда искомое отношение равно
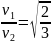 .
.
