- •Министерство образования и науки российской федерации
- •Содержание:
- •Кинематика поступательного и вращательного движения
- •Динамика поступательного и вращательного движения.
- •Работа. Энергия
- •Законы сохранения в механике
- •Элементы специальной теории относительности
- •Средняя энергия молекул
- •Распределения Максвелла и Больцмана
- •Первое начало термодинамики
- •Второе начало термодинамики. Энтропия.
- •Электростатическое поле в вакууме
- •Законы постоянного тока
- •Магнитостатика
- •Явление электромагнитной индукции
- •Электрические и магнитные свойства вещества
- •Свободные и вынужденные колебания
- •Сложение гармонических колебаний
- •Волны. Уравнение волны
- •Энергия волны. Перенос энергии волной
- •Уравнения Максвелла
- •Интерференция и дифракция света
- •Поляризация и дисперсия света
- •Тепловое излучение. Фотоэффект
- •Эффект Комптона. Световое давление
- •Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Спектр атома водорода. Правило отбора
- •Уравнение Шредингера
- •Ядерные реакции
- •Ядро. Элементарные частицы
- •Фундаментальные взаимодействия.
Сложение гармонических колебаний
№
 1
Сопротивление,
катушка индуктивности и конденсатор
соединены последовательно и включены
в цепь переменного тока, изменяющегося
по закону
1
Сопротивление,
катушка индуктивности и конденсатор
соединены последовательно и включены
в цепь переменного тока, изменяющегося
по закону
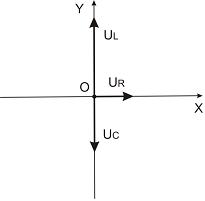
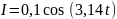 (А). На рисунке представлена фазовая
диаграмма падений напряжения на указанных
элементах. Амплитудные значения
напряжений соответственно равны: на
сопротивлении
(А). На рисунке представлена фазовая
диаграмма падений напряжения на указанных
элементах. Амплитудные значения
напряжений соответственно равны: на
сопротивлении
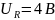 ; на катушке индуктивности
; на катушке индуктивности
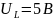 ;
на конденсаторе
;
на конденсаторе
 .
Установите соответствие между
сопротивлением и его численным значением.
.
Установите соответствие между
сопротивлением и его численным значением.
Решение:
Используем
метод векторных диаграмм. Длина вектора
равна амплитудному значению напряжения,
а угол, который вектор составляет с осью
ОХ, равен разности фаз колебаний
напряжения на соответствующем элементе
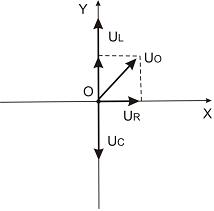
и колебаний силы тока в цепи. Сложив три
вектора, найдем амплитудное значение
полного напряжения:
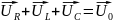 .
Величина
.
Величина
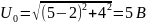 Полное
сопротивление контура найдем по закону
Ома:
Полное
сопротивление контура найдем по закону
Ома: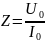 , где U0
,I0
– амплитудные
значения напряжения и силы тока.
Амплитудное значение силы тока, как это
следует из закона его изменения, равно
0,1 А.
Тогда
, где U0
,I0
– амплитудные
значения напряжения и силы тока.
Амплитудное значение силы тока, как это
следует из закона его изменения, равно
0,1 А.
Тогда 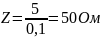 Активное сопротивление
Активное сопротивление
 Полное
сопротивление цепи равно:
Полное
сопротивление цепи равно: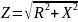 , где
, где
 реактивное
сопротивление; XL
,
XC
– индуктивное
и емкостное сопротивления соответственно.
Отсюда
реактивное
сопротивление; XL
,
XC
– индуктивное
и емкостное сопротивления соответственно.
Отсюда
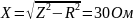
№2 Складываются взаимно перпендикулярные колебания. Установите соответствие между законами колебания точки вдоль осей координат ОХ, OY формой ее траектории.
1.
 2.
2.
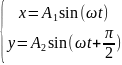 3.
3.
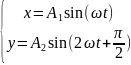
прямая линия
эллипс
фигура Лиссажу
синусоида
Решение:
При
одинаковой частоте колебаний вдоль
осей ОХ,
OY
исключив параметр времени, можно
получить уравнение траектории:
 .
Если разность фаз колебаний
.
Если разность фаз колебаний
![]() ,
то уравнение преобразуется к виду
,
то уравнение преобразуется к виду
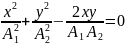 ,
или
,
или
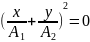 ,
что соответствует уравнению прямой:
,
что соответствует уравнению прямой:
 .
Если
.
Если
 ,
то
,
то
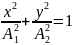 ,
что является уравнением эллипса. Если
складываются колебания с циклическими
частотами mω и
nω,
где m
и
n
– целые
числа, точка М
описывает сложную кривую, которую
называют фигурой Лиссажу. Форма кривой
зависит от соотношения амплитуд, частот
и начальных фаз складываемых колебаний.
,
что является уравнением эллипса. Если
складываются колебания с циклическими
частотами mω и
nω,
где m
и
n
– целые
числа, точка М
описывает сложную кривую, которую
называют фигурой Лиссажу. Форма кривой
зависит от соотношения амплитуд, частот
и начальных фаз складываемых колебаний.
№3 Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами A0 Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
1.

2. 0
3.
1.

2.

3.

4. 0
№4 Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами А0 Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
π/3
π
0

0


Решение
Амплитуда
результирующего колебания, полученного
при сложении двух гармонических колебаний
одного направления с одинаковыми
частотами, определяется по формуле
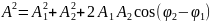 ,
где А1
и
А2
-
амплитуды,
,
где А1
и
А2
-
амплитуды,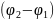 - разность фаз складываемых колебаний.
Если разность фаз
- разность фаз складываемых колебаний.
Если разность фаз
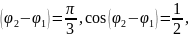 то
то
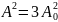 и
и
 Если
Если
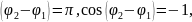 то А=0. Если
то А=0. Если
 то
то
 .
.
№
5
Сопротивление,
катушка индуктивности и конденсатор
соединены последовательно и подключены
к источнику переменного напряжения,
изменяющегося по закону
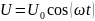 (В).
На рисунке представлена фазовая диаграмма
падений напряжений на указанных
элементах. Установите соответствие
между амплитудными значениями напряжений
на этих элементах и амплитудным значением
напряжения источника.
(В).
На рисунке представлена фазовая диаграмма
падений напряжений на указанных
элементах. Установите соответствие
между амплитудными значениями напряжений
на этих элементах и амплитудным значением
напряжения источника.
5B
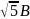
№6 Складываются два гармоничных колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной …
Решение.
Амплитуда
результирующего колебания, полученного
при сложении двух гармонических колебаний
одного направления с одинаковыми
частотами, определяется по формуле
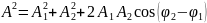 , где
и
, где
и
 -
амплитуда складываемых колебаний;
-
амплитуда складываемых колебаний;
 и
и
 -
их начальные фазы. Следует заметить,
если равны периоды колебаний, то равны
и их частоты, так как
-
их начальные фазы. Следует заметить,
если равны периоды колебаний, то равны
и их частоты, так как
 .
Амплитуда результирующего колебания
будет максимальной, если
.
Амплитуда результирующего колебания
будет максимальной, если
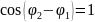 ,
следовательно,
,
следовательно,
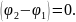
№7 Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами . Если разность фаз складываемых колебаний , то амплитуда результирующего колебания равна …
Ответ: 0
№8
Складываются
два гармонических колебания одного
направления с одинаковыми частотами и
равными амплитудами
. Если
разность фаз складываемых колебаний
 ,
то амплитуда результирующего колебания
равна …
,
то амплитуда результирующего колебания
равна …
Ответ: