
- •1 Вопрос. Предмет изучения теории вероятностей.
- •3. Понятие о событии
- •4. Действия над событиями
- •5. Свойства действий над событиями
- •6.Аксиомы Колмогорова
- •8.Формула классической вероятности
- •9. Принципы и формулы комбинаторики.
- •10. Геометрическая вероятность.
- •11. Относительная частота и вероятность
- •12. Условная вероятность
- •13. Независимость событий
- •14.Вероятность хотя бы одного события
- •15. Формула полной вероятности
- •16. Формула Байеса
- •17. Формула Бернулли
- •18. Предельные формула. Локальная формула Лапласса. Интегральная формула Лапласса. Формула Пуассона
- •20. Случайные величины
- •21. Функция распределения
- •22. Дискретные случайные величины
- •23. Примеры дискретных распределений: Пуассона, биноминальное
- •24. Непрерывные случайные величины. Плотность вероятностей
- •25. Примеры непрерывных распределений: равномерное, показательное, нормальное
- •26. Числовые характеристики случайных величин: математическое ожидание
- •27. Дисперсия и среднеквадратичное отклонение
- •28. Числовые характеристики некоторых дискретных распределений
- •31. Закон больших чисел. Лемма; неравентсво и теорема Чебышева
- •32. Закон больших чисел в форме Бернулли
- •33. Центральная предельная теорема
20. Случайные величины
Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения – соответствующими малыми буквами (xi, yi,…).
Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.
Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно ( соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой – все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.
Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.
21. Функция распределения
Определение 4.4. Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:
F (x) = p (X < x). (4.1)
Свойства функции распределения.
0 ≤ F(x) ≤ 1. Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность.
Функция распределения является неубывающей функцией, то есть F(x2) ≥ F(x1) при х2 > x1. Это следует из того, что F(x2) = p(X < x2) = p(X < x1) + p(x1 ≤ X < x2) ≥ F(x1).
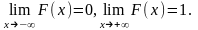 В частности, если все возможные значения
Х лежат на интервале [a,
b], то F(x)
= 0 при х ≤ а и F(x)
= 1 при х ≥ b.
Действительно, X <
a – событие
невозможное, а X <
b – достоверное.
В частности, если все возможные значения
Х лежат на интервале [a,
b], то F(x)
= 0 при х ≤ а и F(x)
= 1 при х ≥ b.
Действительно, X <
a – событие
невозможное, а X <
b – достоверное.Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала:
p ( a < X < b ) = F(b) – F(a).
Справедливость этого утверждения следует из определения функции распределения (см. свойство 2).
Для дискретной случайной величины значение F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.
