7. Представление пространственных кривых.

параметрически.

Непараметрическое явное задание:

Непараметрическое неявное задание - кривая на пересечении двух поверхностей:

Параметрическое задание:

Простейший пример - цилиндрическая спираль:

- радиус, - шаг спирали.

Очень часто аналитическое описание неизвестно. В этом случае ставится задача проведения кривой через ряд заданных точек, или проведения кривой, имеющей более сложную зависимость от заданных точек.

8. Кубические сплайны. Кривые Безье. В-сплайны. Кубические сплайны.

Математически сплайн описывается полиномом  - той степени. Чаще всего используют полиномы третьей степени - кубические сплайны. Конкретный вид кубического сплайна определяется координатами точек, через которые его надо провести (концевых точек) и наклоном в этих точках.

Если требуется провести гладкую кривую между точками, то используется совокупность сплайнов - так называемые сплайновые сегменты. При этом предъявляется требование непрерывности второго порядка в местах соединений.

Уравнение единственного кубического сплайнового сегмента в параметрической форме выглядит следующим образом:

, где - вектор положения произвольной точки на сплайне.

Коэффициенты определяются координатами концов сегмента ( и ) и касательными векторами на концах и , которые являются произвольными по параметру .

Внутри сплайнового сегмента параметр меняется от до ( соответствует ).

Обычно полагают . Тогда

Отсюда получим

Окончательно имеем

,

Отсюда уравнение одного кубического сплайнового сегмента:

Кубические сплайновые кривые широко распространены, однако имеют ряд недостатков. Например, с их помощью нельзя точно передать дугу окружности, а только приближенно. Примеры:

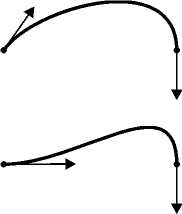
КРИВЫЕ БЕЗЬЕ

Кривая Безье определяется несколькими точками – так называемыми вершинами многоугольника. При этом кривой принадлежат лишь первая и последняя точки, а остальные задают ее форму.

В методе Безье порядок любого криволинейного сегмента может быть увеличен путем задания дополнительных вершин.

Математически кривая Безье описывается полиномиальной функцией, построенной в так называемом базисе Бернштейна. Базисная функция в нем задается соотношением

, где ,

Здесь - степень полинома; – порядковый номер отдельной вершины.

Точки кривой в базисе Бернштейна задаются как

,

то есть -й порядок полинома характеризуется – й вершиной.

В начальной точке

,

В конечной точке

То есть и , вершины и действительно являются началом и концом криволинейного сегмента.

В-СПЛАЙНЫ

Еще одним методом гладкой кривой между двумя точками (концами), форма отдельных участков которой определяется промежуточными точками, является метод В-сплайнов. Вначале определим понятие В–сплайна. Произвольная точка кривой ,то есть ее вектор положения, задается в В-сплайн базисе следующим образом:

Здесь - вершины характеристического многоугольника, ; – базисные функции; - порядок кривой; – параметр, изменяющийся в диапазоне от 0 до В отличие от метода кривых Безье, где в методе В-сплайнов величина и определяется порядком кривой, а также наличием так называемых кратных вершин

Для определения базисных функций введем понятие узлового вектора. Узловой вектор или вектор параметрических узлов представляет собой последовательность целых положительных чисел

в которой . Примерами узлового вектора является или и т. д. Значения рассматриваются как параметрические узлы, характеризующие различные интервалы изменения параметра . Размерность узлового вектора и конкретные значения узлов зависят от числа вершин задающего многоугольника, то есть от , порядка кривой и сложности вершин.

Сложная (или кратная) вершина это две или более вершины с одинаковыми координатами. В узловом векторе сложным вершинам соответствует последовательность одинаковых по величине компонент , где – кратность вершины.

Алгоритм формирования узлового вектора следующий. Входными параметрами являются:

1. массив вершин задающего многоугольника, в котором - кратная вершина представлена как - простых вершин с совпадающими координатами - массив ;

2. – число вершин без l;

3. – порядок кривой.

На выходе формируется вектор . Размерность вектора определяется, как , то есть

1. Для ;

2. Для , если , то если , то

3. Для

Отметим одно общее правило: начальные и конечные вершины условно считываются - кратными, однако, в отличии от кратных промежуточных вершин, это не приводит к увеличению , а лишь отражается в узловом векторе.

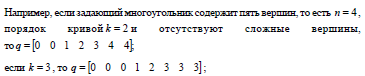
Теперь определим базисные функции . Они задаются рекуррентным соотношением

отсюда видно, что если порядок кривой равен , то функция , соответствующая i- вершине , не равна нулю только на промежутке то есть каждая вершина имеет ограниченное (локальное) влияние на форму кривой. Если порядок кривой равен числу вершин и отсутствуют сложные вершины, то В-сплайн кривая совпадает с кривой Безье; с уменьшением порядка форма кривой приближается к форме описывающего ее многоугольника.

При кривая полностью совпадает с многоугольником. При k = 4 – это кривая Безье; при k = 3 – промежуточное положение.

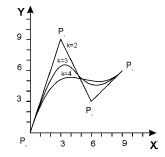
Чем выше порядок, тем больше форма кривой отличается от формы задающего многоугольника.