12

1. Преобразования для точек и прямых линий.

Преобразование точек

Пусть на плоскости т. Р . Исходные координаты точки Р(х,у) преобразованы в , где .

1) a=d=1, b=c=0 положение точки не изменилось.

2)

Происходит изменение масштаба по оси: или перемещение точки по оси . Если , то масштаб увеличивается (перемещение вправо); если -масштаб уменьшается (перемещение влево). Если , то происходят подобные изменения, но с отображением относительно оси .

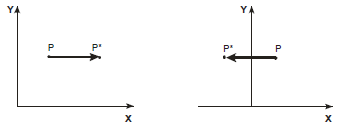
3) В данном случае происходят изменения масштаба по оси , и отображение (если ) относительно оси .

4)

Изменение масштаба (перемещение) по обеим осям (если , то не одинаково), отображение, если или , то относительно осей или соответственно, а если вместе, то относительно начала координат.

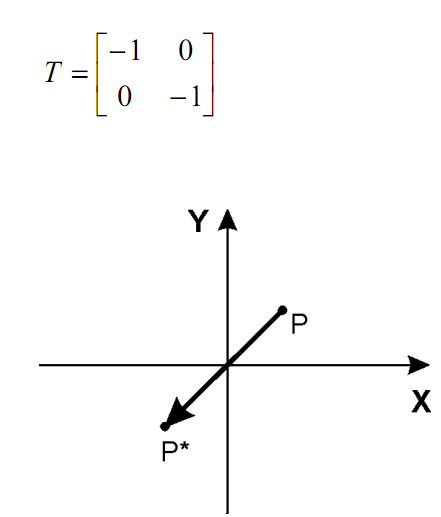
5)

Координата точки не изменяется, а координата линейно зависит от начала координат. Этот эффект называется сдвигом

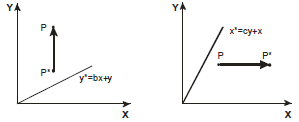
6)

Сдвиг вдоль оси пропорционально начала координате

Преобразование прямых линий

Прямая линия может быть задана координатами двух ее точек. Отрезок прямой задается координатами его концов. Пусть координаты концов отрезка равны

В результате преобразования получим

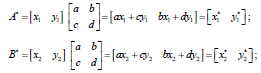
Преобразование отрезка можно записать представив его в виде матрицы координат концов

Тогда преобразованный отрезок получится как

матрица преобразования преобразует прямую линию в другую прямую. Между точками исходного и преобразованного отрезка существует взаимно однозначное соответствие. Концы отрезка преобразуются в концы нового отрезка. Средняя точка преобразуется в среднюю точку.

Координаты средней точки исходного отрезка равны:

преобразованного отрезка

Применение преобразования к точке дает ,

точку . Это соответствие выполнится для любой точки отрезка, делящей его в отношении , т. е. вообще для любой точки отрезка.

При применении машинной графики, чтобы получить преобразованный отрезок, необходимо преобразовать его концы и соединить полученные точки.

2.Вращение, отображение, изменение масштаба, произвольная матрица вращения. Композиция преобразований.

Преобразование матрицей плоских фигур.

Вращение

Вращение вокруг начала координат против часовой стрелки на угол реализуется матрицей Н

а угол – матрицей

На угол – матрицей

Вращение осуществляется вокруг оси, перпендикулярной к плоскости .

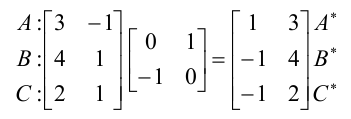
2.1.1Отображение

Отображение определяется поворотом на вокруг оси, лежащей в плоскости .

Отображение относительно оси осуществляется матрицей

Относительно оси – матрицей

Относительно оси – матрицей

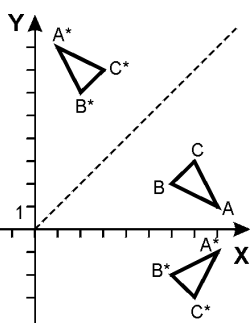
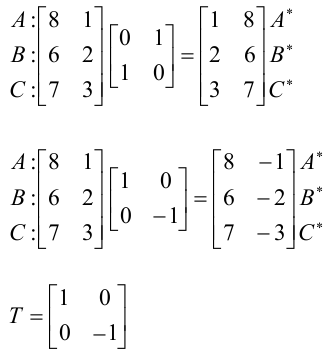
Изменение масштаба

Изменение масштаба определяется значением элементов главной диагонали матрицы 22 Если элементы главной диагонали матрицы не равны, то происходит искажение формы.

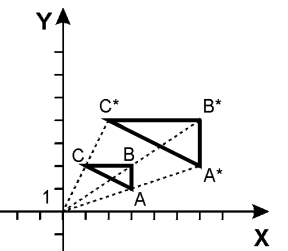
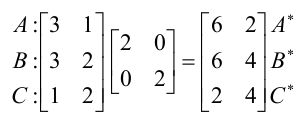
Произвольная матрица вращения 2x2

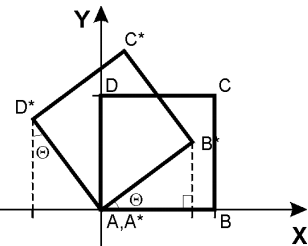
На примере единичного квадрата получим общий вид матрицы вращения на угол .В случае преобразования единичного квадрата координаты точки определяют первую строку матрицы, а точки – вторую строку. Таким образом, матрица вращения на произвольный угол определяется как

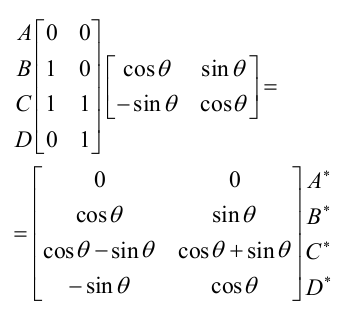
Частные случаи, рассмотренные выше, легко получаются подстановкой значений .