Лекція 2. Розв’язування систем лінійних алгебраічних рівнянь.

1. Постановка задачі

2. Метод Жордана-Гаусса

3. Ітераційні методи

1. Постановка задачі

Прикладні задачі часто зводяться до багатовимірних у загальному випадку нелінійних рівнянь, що розв’язують методом лініарізації, тобто приведенням нелінійних рівнянь до лінійних. У загальному випадку система n рівнянь з n невідомими записується у вигляді:

(1)

(нелінійна система досить складна при ,

лінійна при )

Ми будемо розглядати окремий випадок системи (1), а саме

систему з n лінійних неоднорідних рівнянь:

(2)

(система в якій кількість невідомих = кількості рівнянь називається нормальною)

або в матричній формі ,

де ; ; 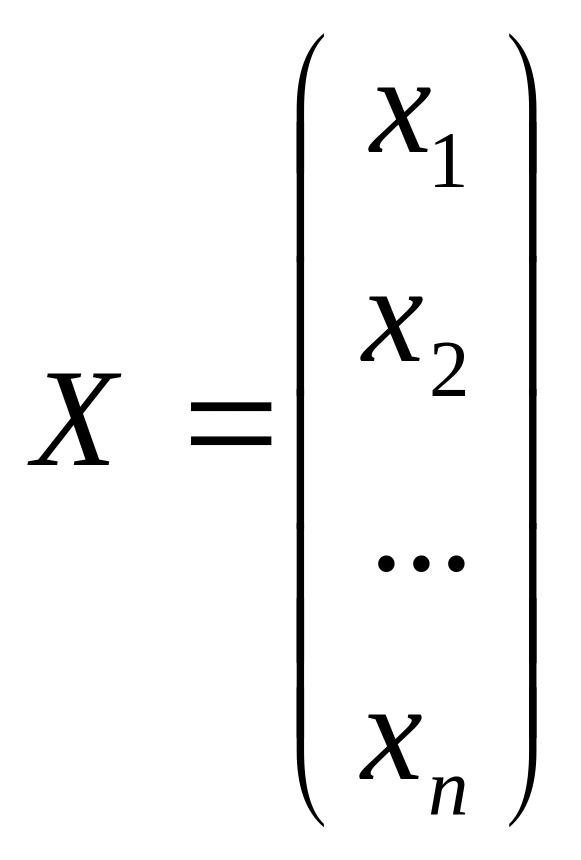; 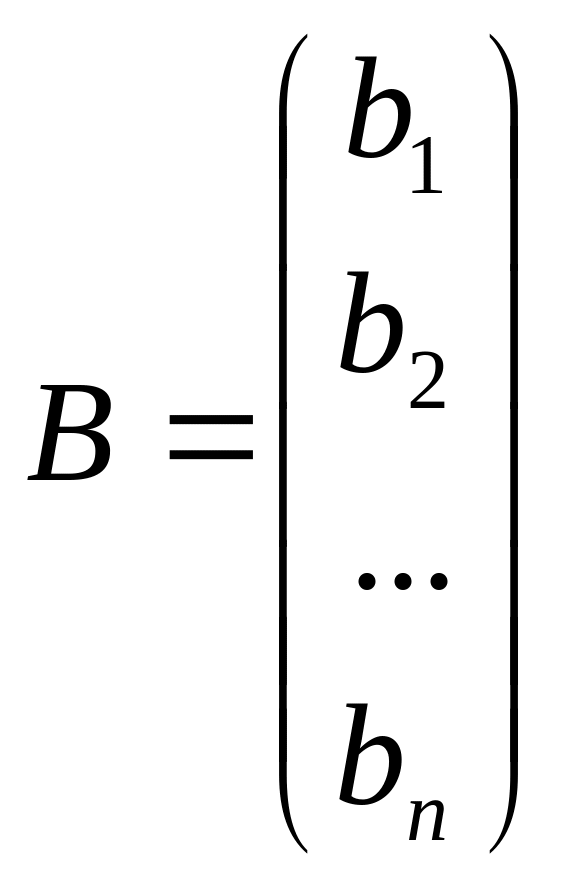( ) (3)

Характер задачі і точність отриманого розв’язку у більшості залежить від її обумовленості.

Задача є добре обумовленою, якщо при невеликих /незначних/ змінах вхідних даних результат її розв’язку змінюється несуттєво /несильно/ та при будь-яких вихідних даних з можливого діапазону задача однозначно розв’язується .

Наведемо приклад погано обумовленої задачі.

Приклад 1.

Нехай задана система

З’ясувати, чи є ця задача добре обумовленою.

Розв’язання: Система має точний розв’язок: ,

Нехай одне з вихідних значень змінилося на долі відсотка

І для нової системи будемо мати розв’язки: ; . Отже, компоненти розв’язку змінилися в 3 та 4 рази задача є погано обумовленою.

Пояснимо поняття обумовленості СЛАР на графіку (знову для простоти) для системи з двох рівнянь

Точним розв’язком є вектор . Графічно це координати точок перетину прямих заданих рівнянь:

та

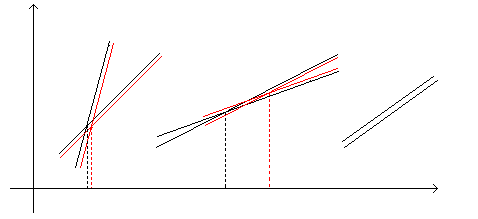
На малюнку, відповідно до трьох наборів вхідних даних, заданих з деякими похибками і відповідних різним системам лінійних рівнянь, ілюструється характер обумовленості системи. Якщо суттєво відрізниться від 0, то точка перетину пунктирних прямих, зсунутих відносно прямих через похибки задання А та b, зсувається несильно. Це говорить про добру обумовленість системи.

При незначні похибки в коефіцієнтах можуть привести до великих похибок у розв’язку (погано обумовлена задача), так як самі прямі близькі до паралельних.

При прямі або паралельні або співпадають, і тоді розв’язок або не існує, або не є єдиним.

Більш строго обумовленість задачі характеризується числом обумовленості

, де (одна з можливих норм)

Чим більшим є це число, тим гіршою є обумовленість системи.

Підкреслимо, що реалізація добре або погано обумовленої задачі напряму пов’язана із стійкістю розв’язку.

Чисельний метод називається стійким, якщо результати обчислення залежать від вхідних даних і похибка округлення пов’язана з реалізацією чисельного метода, при заданих межах змін параметрів чисельного метода, залишається обмеженою.

Мають місце 2 класи чисельних методів розв’язування СЛАР:

1. прямі методи, що дозволяють знайти розв’язок за певне число операцій. До прямих методів відносяться: метод Гауса та його модифікації, метод LU- розкладання (метод Холецького) та інші.

2. ітераційні методи, основані на використанні циклічного процесу, що дозволяють одержати розв’язок, як результат послідовних наближень. До ітераційних методів відносяться: метод простих ітерацій, метод Зейделя та інші.