I. Введение

Построение трехслойных, а также многослойных кривых вертикально­го электрического зондирования расчётным путём требует большой кро­потливой и трудоёмкой работы со счётными машинами. Несмотря на то, что число кривых ВЭЗ, рассчитанных аналитическим путём, достаточно велико, тем не менее, количество последних иногда бывает недостаточным для интерпретации полевых кривых ВЭЗ вследствие многообразия распре­деления сопротивлений и мощностей слоев геологического разреза. По­следнее обстоятельство и побудило разработать наиболее простые методы построения кривых ВЭЗ – графические, позволяющие очень просто и быст­ро создавать необходимые кривые. Сопоставления кривых, рассчитанных и настроенных графически, показывает, что погрешности при графических построениях могут достигать иногда на отдельных участках кривой 5-10% и более. Тем не менее это не исключает возможности использования графически построенных кривых ВЭЗ при истолковании практических кривых электрозондирования, поскольку измерения _к в полевых условиях производятся с погрешностью до 5%, а иногда и более.

К построению кривых ВЭЗ нередко прибегают при проектировании электроразведочных работ, т.к. даже при ориентировочных сведениях о параметрах разреза представляется возможным предугадать вид кривых ВЭЗ и выяснить рациональность постановки ВЭЗ в предполагаемых физико-геологических условиях.

Знакомство с методом графического построения кривых ВЭЗ является весьма полезным и с точки зрения качественной интерпретации кривых вертикального электрозондирования. Суть дела заключается в том, что в процессе построения, получая искомую кривую как кривую, состоящую из трех звеньев, интерпретатор глубже познает взаимовлияние параметров разреза на общую конфигурацию кривой. Это обстоятельство позволяет ему при визуальном анализе интерпретируемой кривой по её конфигурации делать наиболее правильные качественные выводы о параметрах разреза, что особенно важно в этом случае, когда количественная интерпретация данной кривой ВЭЗ по ряду причин не возможна.

Из всего сказанного следует, что искусством построения кривых ВЭЗ графическим методом должен владеть каждый электроразведчик, зани­мающийся постановкой электрозондирований, тем более, что это не сос­тавляет особого труда, т.к. приемы построения весьма просты. Наиболь­шей простотой отличается методика построения, разработанная А.М. Пылаевым, которая в основном и излагается в данном руководстве. Предполагается, что лицо, приступившее к изучению приемов построения кривых ВЭЗ, уже знакомо с содержанием альбома теоретических кривых вертикальных электрических зондирований, составленного под руководством А.М. Пылаева.

II. Продольная проводимость и поперечное сопротивление

При построении кривых электрозондирования приходиться оперировать с понятиями суммарной продольной проводимости и суммарного поперечного сопротивления. Рассмотрим сущность этих понятий.

Пусть мы имеем столбик с основанием, равным 1 м² (рис. 1) и высотою h, вырезанный из среды, состоящей из m слоев мощностью h_i, с удельным сопротивлением _i, где i – номер слоя и .

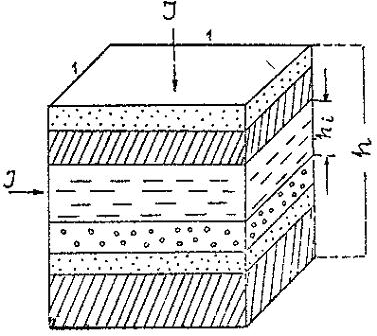
Рис. 1

Если через такой столбик пропускать ток параллельно слоям, то все слои образуют собою систему параллельно включенных проводников, каждый из которых обладает сопротивлением:

.

Величина обратная сопротивлению есть проводимость, которая при указанном направлении тока называется продольной и обозначается буквою ***.

.

Проводимость системы параллельно включенных проводни­ков, как известно, равна сумме проводимостей, откуда суммарная продоль­ная проводимость столбика будет иметь следующее выражение:

.

Если мы будем пропускать ток в направлении перпендикулярно основанию столбика, состоящего из тех же слоев, то поперечное сопротивление Т, оказываемое слоистым столбиком току, можно вычислить как сопротивление системы последовательно включенных проводу с поперечным сечением, равным единице, длиной h_i и удельным сопротивлением _i каждого про­водника, поэтому

,

где Т – суммарное поперечное сопротивление в Омм²,

m – число слоев;

Т_i –сопротивление i-го слоя в Омм².

В случаях изотропной среды знание продольной проводимости S и поперечного сопротивления Т столбика, вырезанного из этой среды, может заменить знание  - удельного сопротивления этой среды и h – высоты этого столба. Действительно, из формул

, (1) и Т=h, (2)

непосредственно следует, что

.

Поскольку при изображении результатов электрозондирования исполь­зуется билогарифмический масштаб, представим уравнения (1) и (2) в билогарифмических координатах, откуда имеем:

lgS=lgh – lg; lg=lgh – lgS;

lgT=lgh – lg; lg=lgT – lgh;

Обозначив lgh=, lg=, получим:

=– lgS (3)

=–+lgT (4)

Уравнение (3) является уравнением прямой, наклоненной под углом 45^о к оси ординат и отсекающей на отрицательных осях координат отрезок, рав­ный lgS. Уравнение (4) есть также уравнение прямой, но наклоненной к оси абсцисс под углом 135^о и отсекающей на отрицательной оси ординат и положительной оси абсцисс отрезки, равные lgТ (рис. 2).

Рис.2