Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Задачи рейтинг ОТЦ.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

5.45 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 174 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

2. Расчет линейных цепей с сосредоточенными параметрами при произвольном воздействии. Переходные процессы

2.1. Методы анализа неустановившихся и переходных процессов в линейных цепях

В задачах анализа переходных процессов, в линейных электрических цепях с сосредоточенными параметрами приходится рассчитывать мгновенные значения напряжений и токов в элементах цепи, т.е. функции времени. Переходным называется процесс, возникающий в электрической цепи при переходе от одного установившегося состояния к другому. Переход от одного состояния цепи к другому может быть вызван негармоническим воздействием,

подключением или отключением внешнего источника, изменением структурной схемы цепи или изменением ее параметров, т.е. коммутацией. При расчетах можно полагать, что коммутация происходит мгновенно. Исходным положением для анализа переходного процесса в линейных электрических цепях является то, что переход реальной цепи, содержащей реактивные элементы, от одного установившегося режима к другому не может происходить мгновенно.

Известны следующие основные методы расчета переходных процессов:

1 Классический метод или метод решения неоднородного линейного дифференциального уравнения [1],[9].

2 Операторный метод или метод преобразования Лапласа [1],[2],[10].

3 Метод преобразования Фурье и рядов Фурье [3].

4 Метод интеграла Дюамеля [1],[4].

5 Метод дискретных преобразований [5].

6 Метод переменных состояния или пространства состояния[6].

7 Численные методы [7].

2.2 Применение классического метода

Законы коммутации и начальные условия

При решении уравнений переходных процессов следует использовать свойства непрерывности заряда емкости и потокосцепления индуктивности во времени. Эти свойства носят название законов коммутации.

Из законов коммутации следует:

(13)

Это можно сформулировать следующим образом: потокосцепление в индуктивности и заряд на емкости не могут изменяться скачком. Записанные соотношения позволяют использовать начальное состояние цепи (начальные условия) для определения неизвестных постоянных интегрирования в уравнениях переходных процессов.

При отсутствии источников бесконечной мощности суммарная запасенная в цепи энергия может изменяться только плавно, т.е. представляет собой непрерывную функцию времени. Это позволяет сделать вывод о неизменности в первое мгновение после коммутации t=0₊ суммарных потокосцепления и заряда в цепи по отношению к их значениям в мгновение перед коммутацией t=0_-:

(2.1)

Если при коммутации не производится подключения или отключения ветвей, содержащих L и C, то из (2.1) следует непрерывность токов индуктивностей и напряжений емкостей (в первое мгновение эти параметры неизменны, а затем плавно изменяются, начиная со своих значений) – первый и второй законы коммутации:

i_L(0₊)=i_L(0_-), u_c(0₊)=u_c(0_-). (2.2)

При этом i_C , u_L , i_R , u_R могут изменяться произвольно, в том числе и скачкообразно.

Алгоритм расчета переходного процесса классическим методом:

При анализе переходного процесса в линейных инвариантных во времени цепях с сосредоточенными параметрами классическим методом необходимо провести:

Анализ цепи до коммутации (определение независимых начальных условий i_L, u_С при ).
Определение i_L, u_C при с помощью законов коммутации или принципа непрерывности потокосцепления и заряда.
Составление дифференциального уравнения цепи после коммутации при t 0 (относительно искомого i_L, или u_C ):

. (2.3)

Определение свободной составляющей реакции цепи (составление характеристического уравнения цепи, определение его корней и общего вида свободной составляющей – общего решения ОДУ):

, (2.4)

(2.5)

когда все корни уравнения (2.4) простые (различные);

(2.6)

для корня p_k характеристического уравнения (2.4) кратностью n;

при наличии комплексно-сопряженных корней в уравнении (2.4)

( - собственное затухание, частота свободных колебаний) составляющая свободного тока, обусловленная этими корнями характеристического уравнения, находится из соотношения

(2.7)

Постоянные , определяются из начальных условий по искомой переменной и ее производной:

Анализ установившегося процесса в цепи после коммутации при (отыскание принужденной составляющей реакции цепи – частного решения ДУ цепи):

.(2.7)

Нахождение общего вида реакции цепи (общее решение ДУ – суммирование свободных и принужденных составляющих):

(2.8)

Определение постоянных интегрирования , которые находятся по независимым начальным условиям – значениям i, u и их первым производным при t = 0.
Определение реакции цепи, соответствующей заданным начальным условиям (подставляя постоянные интегрирования в общее решение ДУ цепи находим его решение, соответствующее заданным начальным условиям, т.е. i либо u одной из ветвей при t >0).

Основные расчетные соотношения

Для переходных процессов в линейных R , L , С - цепях можно записать линейные дифференциальные уравнения, решение которых позволяет найти токи i( t) и напряжения u(t) в этих цепях во время переходного процесса:

для активного сопротивления

(1)

для индуктивности

(2)

для емкости

(3)

Здесь использована символическая запись соотношений для токов и напряжений на элементах, в которых операция интегрирования заменена символический оператор I/p — , операция дифференцирования - на оператор р – . Символическая запись уравнений позволяет легко составлять дифференциальные уравнения, так как по виду не отличаетcя от операторных.

Причем для нахождения установившегося (стационарного) режима достаточно найти частное решение неоднородного линейного дифференциального уравнения (НЛДУ), в правой части которого присутствуют функции внешних воздействий (либо это постоянное напряжение, либо синусоидальная, либо некоторая периодическая функция). Частное решение неоднородного линейного дифференциального уравнения определяет установившийся режим цепи или иначе его называют вынужденным режимом. Частное решение обращает уравнение в тождество. Довольно часто его можно найти методом подбора, или любимым методом студентами – методом подгонки решения. Обозначим, например, вынужденный ток - .

Для нахождения переходного процесса необходимо определить полные решения дифференциальных уравнений цепи. Как известно [8], полное решение линейного дифференциального уравнения получается как сумма частного решения неоднородного линейного дифференциального уравнения и полного решения однородного линейного дифференциального уравнения (ОЛДУ), которое получается из того же уравнения цепи, если положить в нем заданные ЕДС (внешние воздействия) равными нулю. Обозначим полное решение ОЛДУ - Оно носит название свободного тока.

Таким образом,

(4)

Если рассматривать асимптотику решения полного тока в цепи, то можно видеть, что при стремлении текущего значения времени к бесконечности полный ток стремится к вынужденному току, а свободный ток к нулю: t — , , . Это происходит потому, что свободный ток находится при отсутствии внешних источников.

Следует отметить, что в цепях с одним энергоемким элементом переходный процесс апериодический. В цепях с малыми потерями, содержащих индуктивность и емкость при коммутации возможно появление колебаний. Это явление наблюдается при отрицательном дискриминанте квадратного характеристического уравнения (корни уравнения комплексно сопряженные).

Для последовательной RLC – цепи это соответствует ее добротности (сопротивление потерь , где – характеристическое сопротивление). При этом свободные колебания в цепи имеют частоту:

, (2.9)

где – резонансная частота цепи, а – коэффициент их затухания.

Сопротивление потерь добротность ( ) соответствует критическому режиму для возникновения колебаний.

Классический метод применяют, когда исследуемая цепь имеет невысокий порядок сложности, а внешнее воздействие после коммутации гармоническое или постоянное.

Анализ переходных процессов в цепях первого порядка классическим методом

Цепями первого порядка будем называть цепи, которые содержат один реактивный элемент (емкость или индуктивность) и одно или несколько активных сопротивлений. Для цепей первого порядка можно записать дифференциальное уравнение первого порядка. Примеры простейших цепей первого порядка приведены на рисунке 2.2.1.

В дальнейшем будем рассматривать входные воздействия e(t) -ЭДС вида импульсных и скачкообразных процессов:

1 e(t)=E₀1(t) - единичная функция включения Хевисайда,

2 e(t)= - дельта-функция Дирака.

3 e(t)= -гармоническая функция.

Используемые функции вида единичной функция включения Хевисайда 1(t) и дельта - функции Дирака (t) определены в [8] .

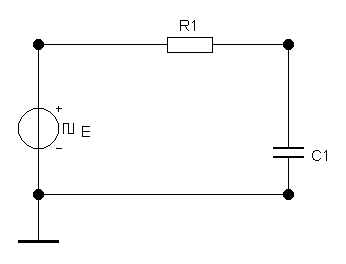
а) интегрирующая RC-цепь первого порядка

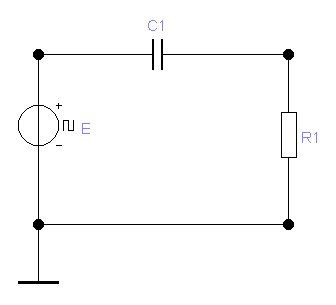
б) дифференцирующая RC-цепь первого порядка

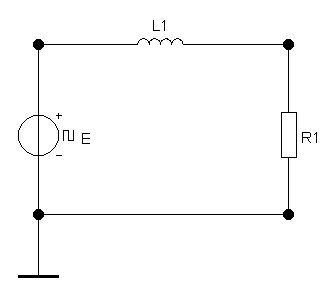
в) интегрирующая RL-цепь первого порядка

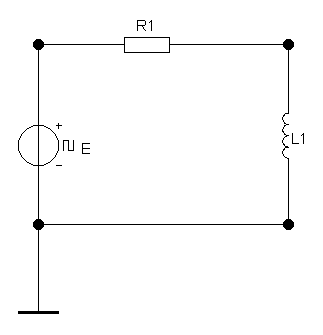
г) дифференцирующая RL-цепь первого порядка

Рисунок 2.1 – Примеры простейших цепей первого порядка

Пример 1

Рассмотрим пример нахождения переходных характеристик в цепи первого порядка при нулевых начальных условиях.

В схеме (рисунок 2.2) в момент t. = 0 ключ замыкается и ЭДС амплитудой Е1=10В подключается к цепи. Определить закон изменения тока во времени. Начальные условия нулевые.

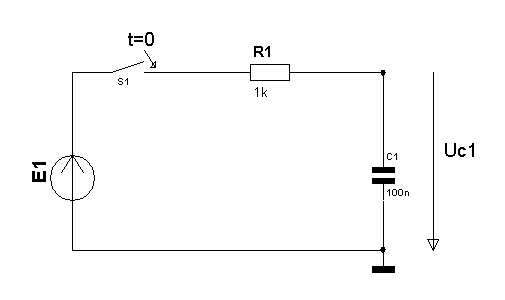
Рис. 2.2. Классический метод анализа переходных процессов в R-C цепи.

Решение задачи классическим методом состоит из следующих этапов:

1 Этап. Анализ цепи коммутации (t< 0 до появления воздействия). В результате этого анализа определяют токи индуктивностей и напряжения на емкостях в момент времени, непосредственно предшествующий появлению воздействия t=0. В рассматриваемом примере задано, что напряжение на емкости в рассматриваемый момент равно нулю: .

2 Этап. Определение независимых начальных условий. Независимые начальные условия представляют собой токи индуктивностей и напряжения на емкостях в момент времени непосредственно после появления воздействия t = 0+. В данном примере Uc(0+)=Uc(0-).

3 Этап. Составление дифференциального уравнения цепи после появления воздействия при t>0.

Для этого на основании второго закона Кирхгофа составим уравнение для контура (рисунок 1.2.2).Наиболее просто дифференциальное уравнение в символической форме составляется с использованием операторного или обобщенного сопротивления цепи:

(14)

(15)

(16)

(17)

(18)

Уравнение неудачно, так как для тока в емкости необходимо находить зависимые начальные условия. При известных навыках это сделать несложно. Но при первом знакомстве лучше использовать независимые начальные условия. Запишем уравнение для напряжения на емкости

(19)

Символическая запись дифференциального уравнения для напряжения на

емкости цепи (рисунок 2.2):

(20)

(21)

(22)

Получили линейное неоднородное дифференциальное уравнение первого порядка.

4 Этап. Анализ установившегося процесса в цепи после коммутации (при t >0). В результате этого анализа находят принужденную составляющую реакции цепи (частное решение неоднородного линейного дифференциального уравнения).

В рассматриваемом примере при падение напряжения на емкости U_c(t) стремится к постоянному напряжению ЭДC E₀, так как ток в цепи при этом будет неограниченно приближаться к нулю. Это следует из того, что для постоянного тока емкость представляет собой разрыв цепи. На основании (22).

где Uc уст (t) - принужденная составляющая решения.

5 Этап. Определение свободной составляющей реакции цепи. На этом этапе составляют характеристическое уравнение, находят его корни и определяют общий вид свободной составляющей реакции цепи (общее решение однородного линейного дифференциального уравнения, полученного из исходного приравниванием к нулю правой части). Уравнение записывается для момента времени непосредственно после коммутации:

(23)

Характеристическое уравнение, соответствующее уравнению (23) имеет вид

(24)

Решение этого уравнения:

- корень характеристического уравнения. Корень характеристического уравнения простой, следовательно,

(25)

Неизвестную постоянную интегрирования А найдем из начальных условий.

6 Этап. Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального уравнения) находят путем суммирования свободной и принужденной составляющих. Для цепи (рис.2.2).

(26)

7 Этап. Определение постоянных интегрирования. Постоянные интегрирования находят по зависимым начальным условиям (значениям искомых токов или напряжений и их n -1 производных в начальный момент времени после коммутации). Для определения зависимых начальных условий используют независимые начальные условия и уравнения электрического равновесия цепи после коммутации. В рассматриваемой задаче задано независимое начальное условие

(27)

Из законов коммутации следует

(28)

откуда постоянная интегрирования А равна

(29)

8 Этап. Определение реакции цепи, соответствующее заданным начальным условиям. Подставляя постоянные интегрирования, в общее решение исходного дифференциального уравнения, находят решение, соответствующее заданным начальным условиям при t >0 .

Подставляя (29) в (25) найдем:

(30)

Данное решение соответствует нулевым начальным условиям. Вид решения показан на рис.2.3 для заданных численных значений:

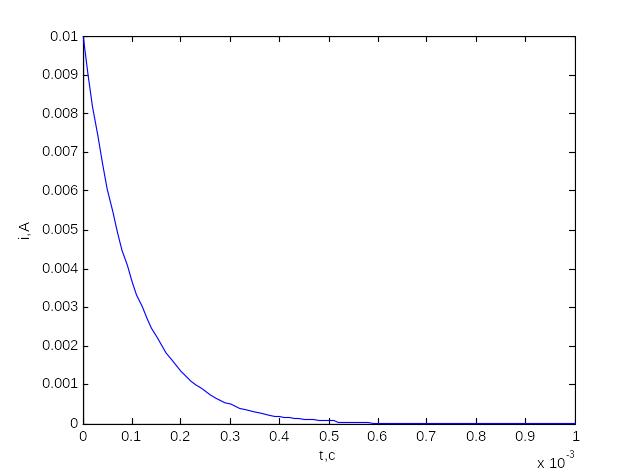
рис. 2.3. График зависимости тока в емкости от времени.

Другим, применяемым для расчетов более сложных цепей является операторный метод, основанный на преобразовании Лапласа.

Это символический метод, в котором операции над функциями времени a(t) заменяются операциями над их символами (изображениями) – A(p). Взаимное соответствие между ними устанавливается с помощью прямого:

, (2.10)

и обратного

(2.11)

преобразований Лапласа и обозначается знаком соответствия a(t) A(p).

Здесь A(p) – изображение оригинала a(t) по Лапласу, p – оператор преобразования Лапласа или комплексная частота.

При использовании метода неизвестные i и u заменяют их операторными изображениями, а элементы цепи – их операторными схемами замещения. По операторной схеме цепи после коммутации составляется система алгебраических уравнений, решая которые находят операторные изображения искомых токов и напряжений. Далее, с использованием обратного преобразования Лапласа, определяются оригиналы для этих изображений. С использованием операторной схемы цепи определяют также операторные входные сопротивления и проводимости:

, , (2.12)

передаточные сопротивления и проводимости:

, , (2.13)

а также коэффициенты передачи по току и напряжению:

, . (2.14)

В теории линейных цепей реакцию на произвольное входное воздействие исследуют также посредством его представления суммой элементарных единичных функций Хевисайда:

(2.15)

и Дирака:

. (2.16)

При этом используется Теорема суперпозиции – свойство линейных инвариантных во времени цепей заключающееся в том, что реакция на сумму входных воздействий равняется сумме реакций на каждое из воздействий в отдельности. Это позволяет ввести такие временные характеристики цепи, как переходная характеристика – реакция на функцию Хевисайда: и импульсная характеристика – реакция на функцию Дирака: . Реакция же цепи на сложное воздействие будет интегральной суммой (интегралом Дюамеля), содержащей переходную и импульсную характеристики:

. (2.17)

Здесь x(t) – воздействие на цепь, а y(t) – ее реакция.

Переходная и импульсная характеристики цепи могут быть определены с использованием классического метода анализа реакции на соответствующие входные воздействия, либо через операторный коэффициент передачи цепи:

. (2.18)

Приведенные соотношения используются при выполнении заданий 1-5 самостоятельной работы №2 и подробно обсуждаются в [2,3]. С примерами решения задач можно ознакомиться в [4, 6].