1.2. Варианты заданий

Вариант №1

1

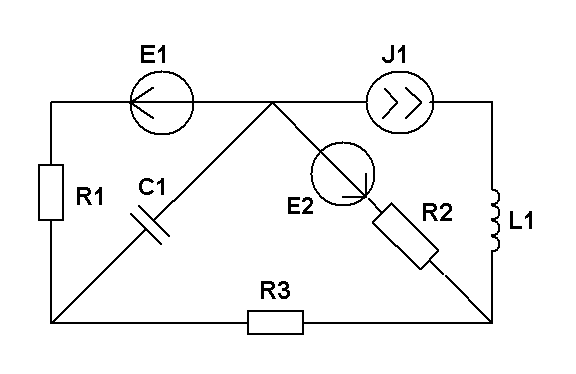
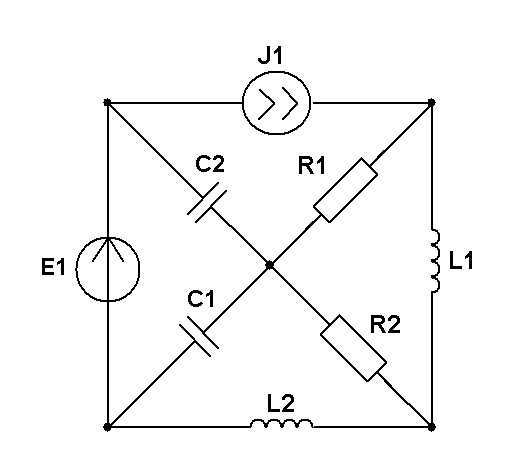
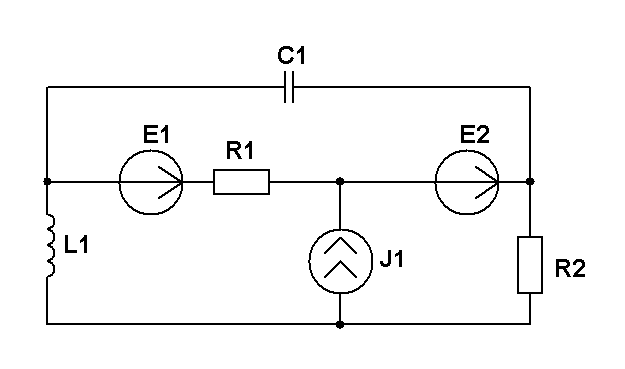
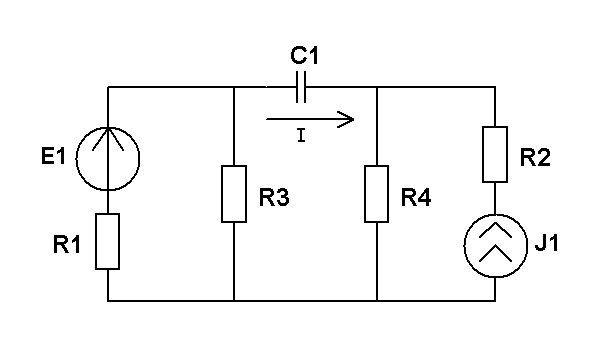
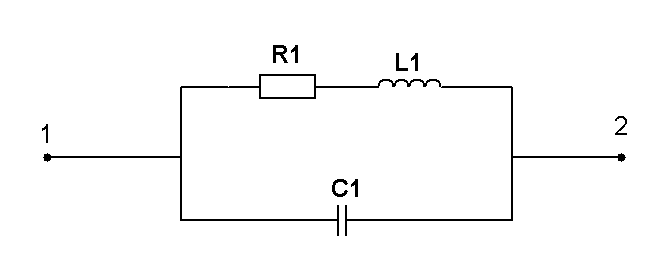
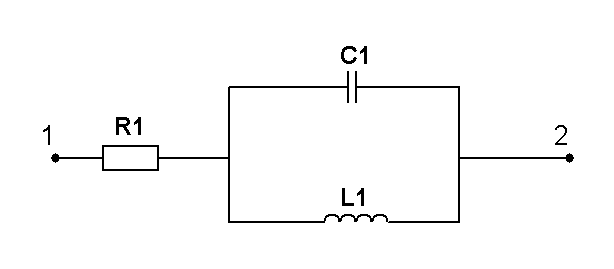
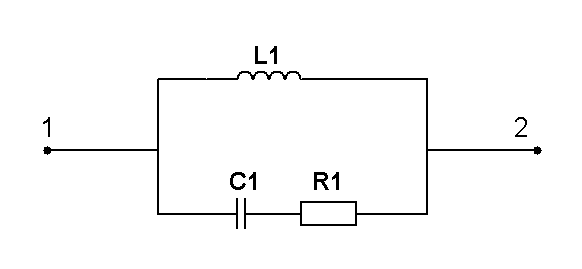
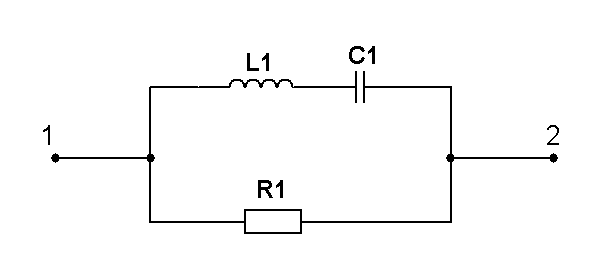
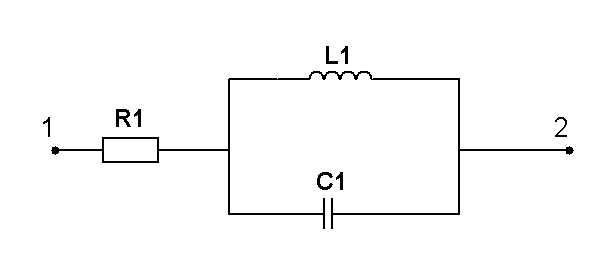
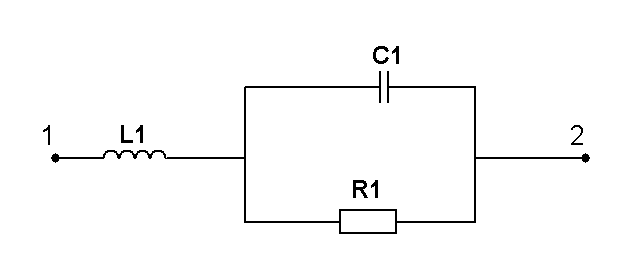
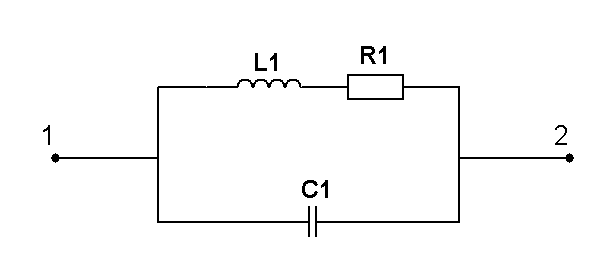
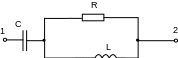
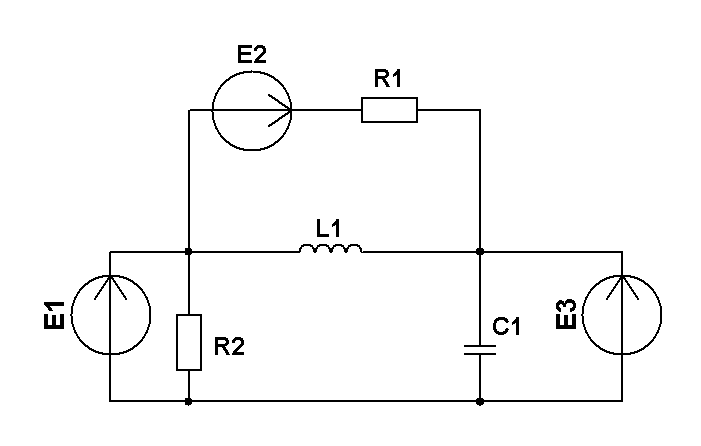
Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

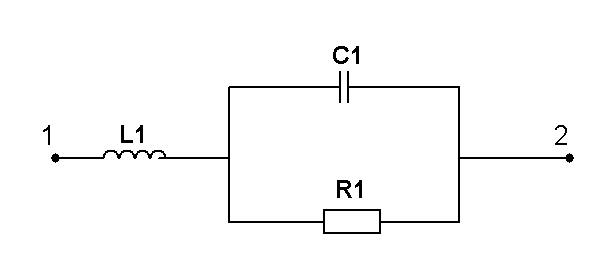
R=2 кОм

L=4 мГн

C=0,4 нФ

=10⁶ рад/с

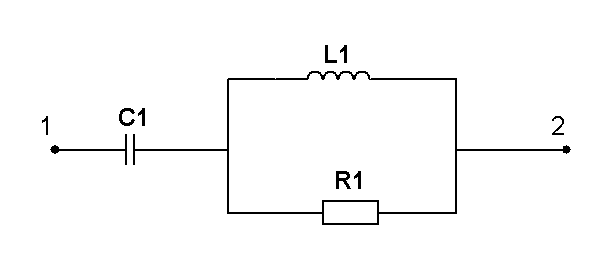
Определить мгновенное значение всех напряжений, если амплитуда напряжения между точками 1 и 2 равна 10 В, а начальная фаза напряжения равна 0. Построить векторную диаграмму для комплексных амплитуд токов и напряжений

3

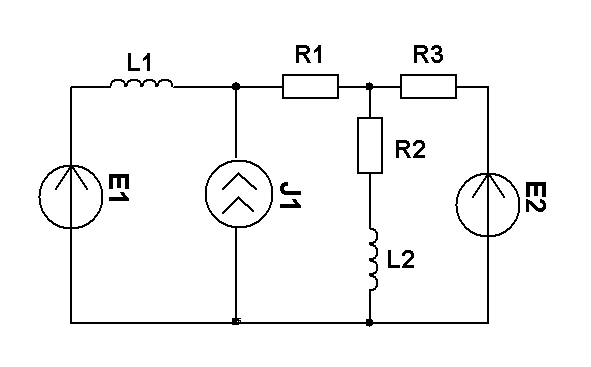
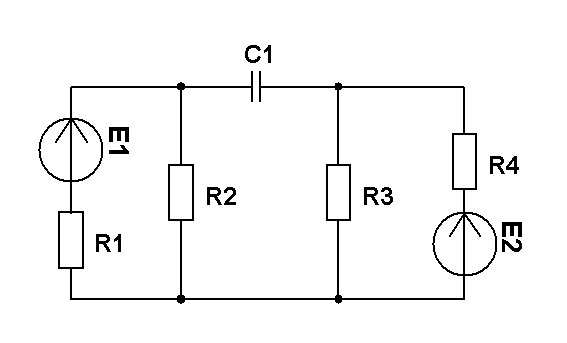
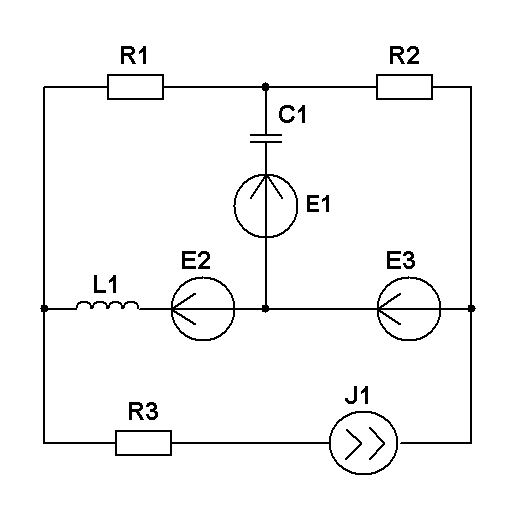
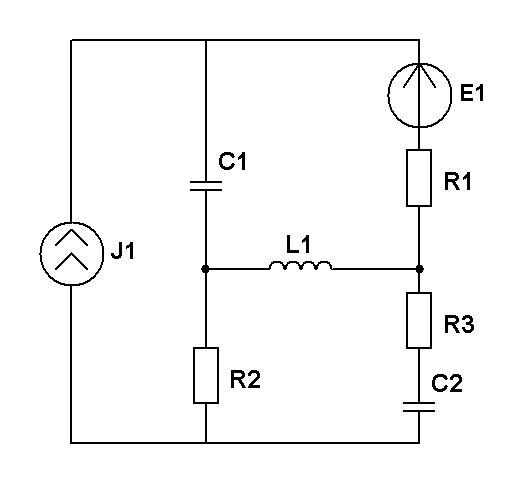
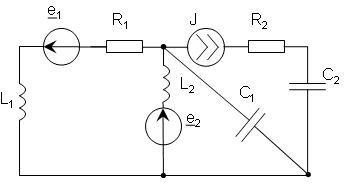
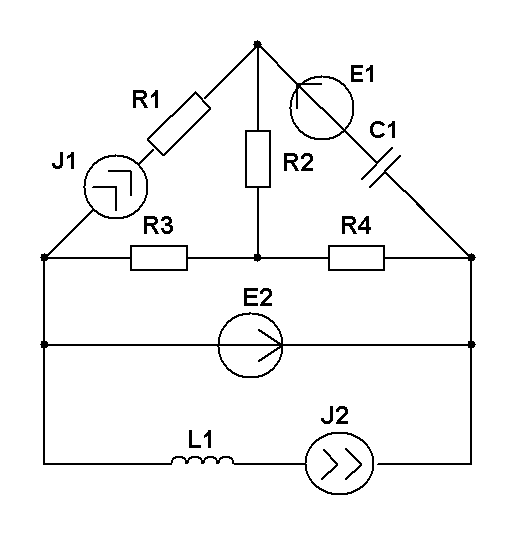
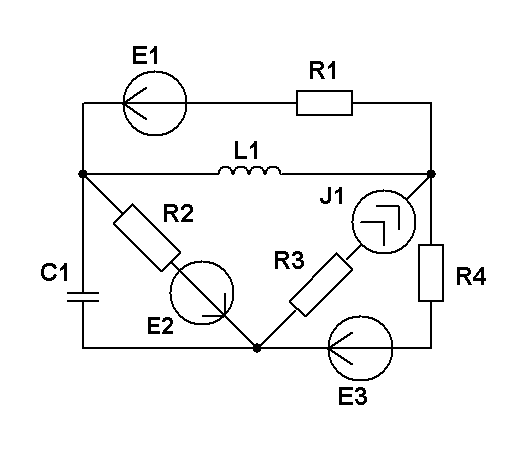
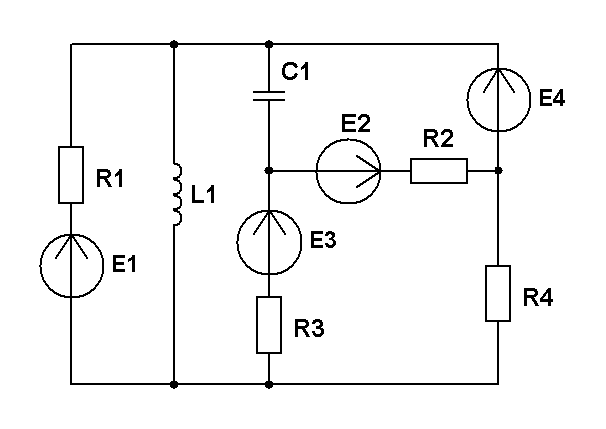
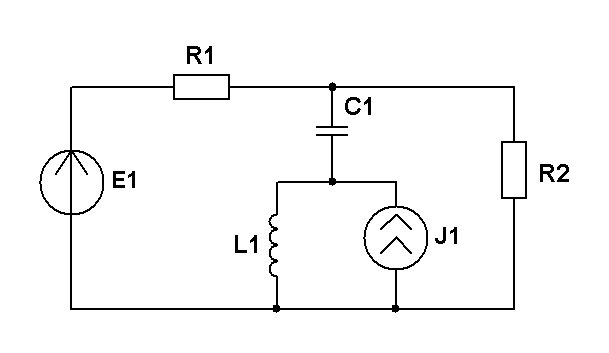
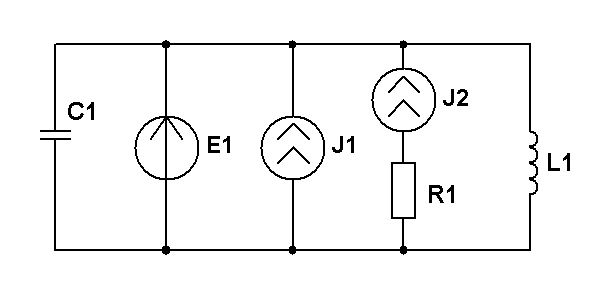
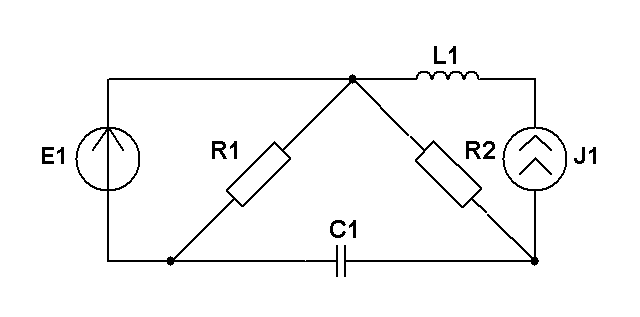
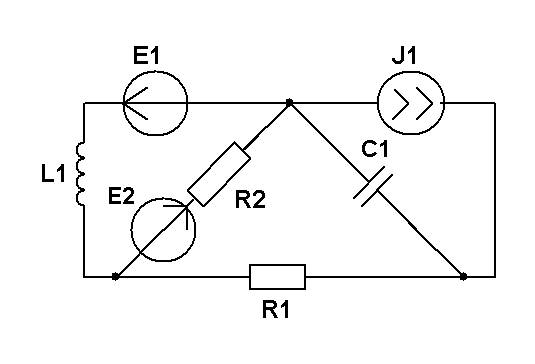
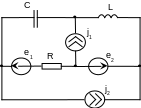
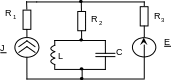
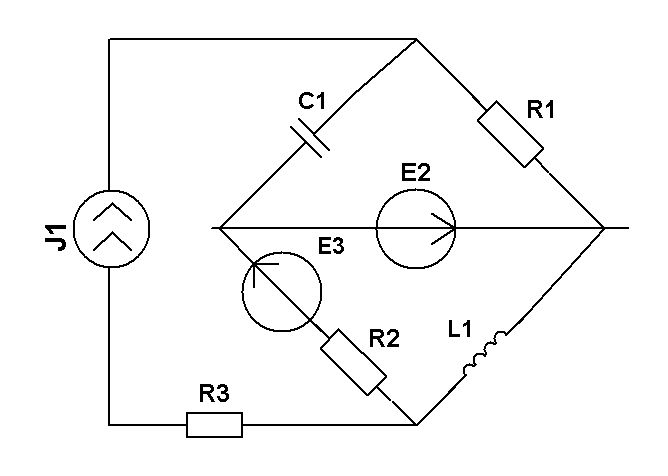
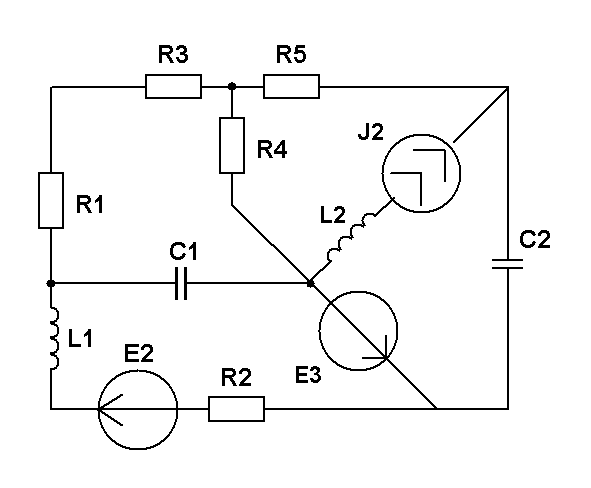
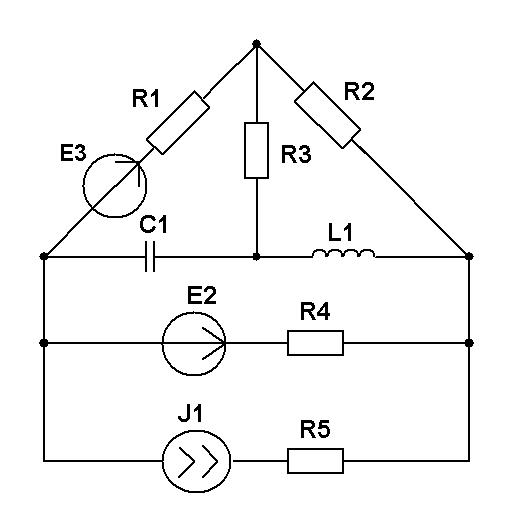
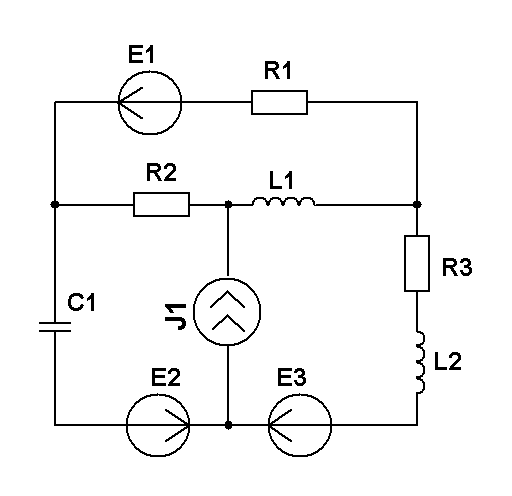
Составить уравнения контурных токов и узловых напряжений и решить их для численных значений: R₁=R₂=R₄= X_C1=100 Ом

R₃=R₅=X_L1= X_L2=25 Ом

E₂(t)=10cost,В;

E₃(t)=5cost, В.;

J₂(t)=20cost, мА

4

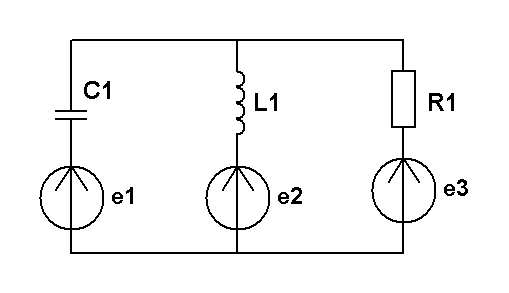
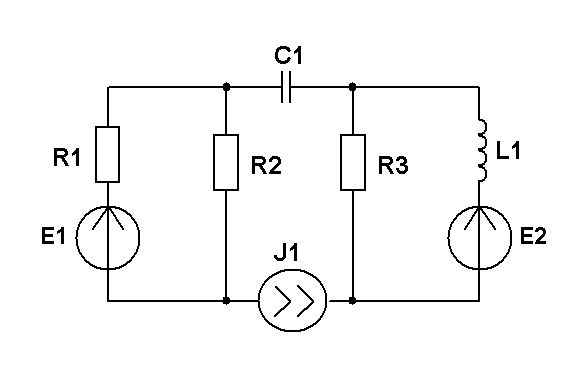
R₁=1 кОм; R₃=2 кОм;

X_L=2 кОм; X_C=3 кОм;

e₁=5 cost, В;

e₂=3 cost, В;

e₃=1 cost, В.

Рассчитать методом наложения ток в индуктивности.

5

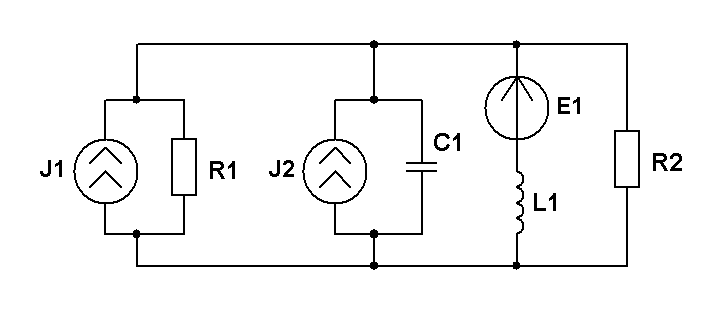
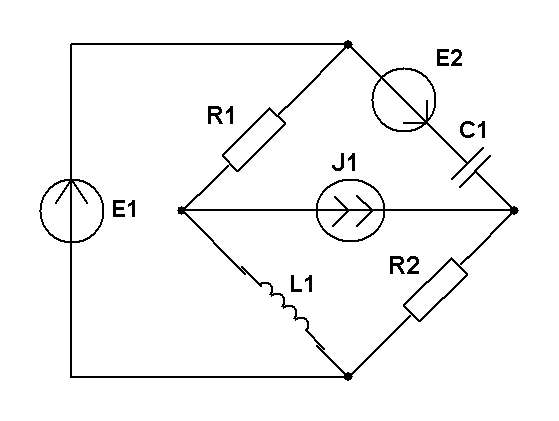
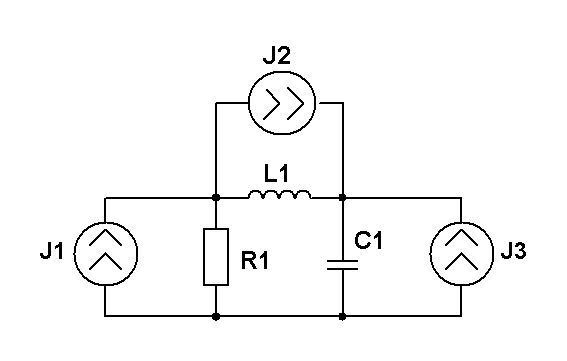
E=25 В; J=0.5 A;

R₁=R₂=100 Ом;

X_L=25 Ом;

X_C=50 Ом.

Методом эквивалентного генератора рассчитать ток в ветви с R₁.

Вариант №2

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=3 кОм

L=6 мГн

C=0,3 нФ

=10⁶ рад/с

Определить мгновенное значение всех напряжений, если U_1-2=15 В.

3

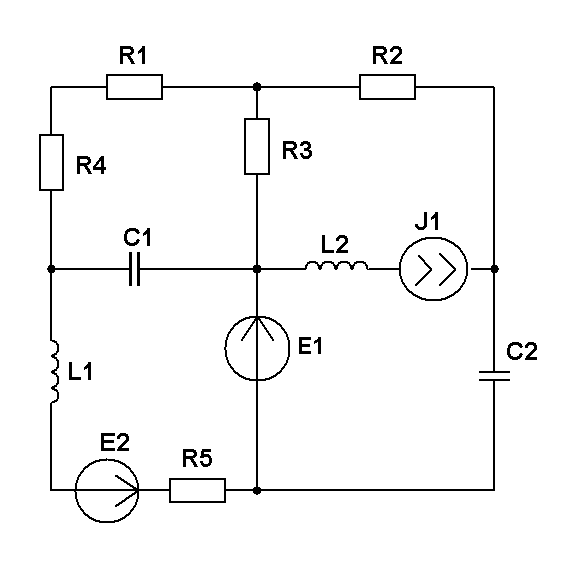
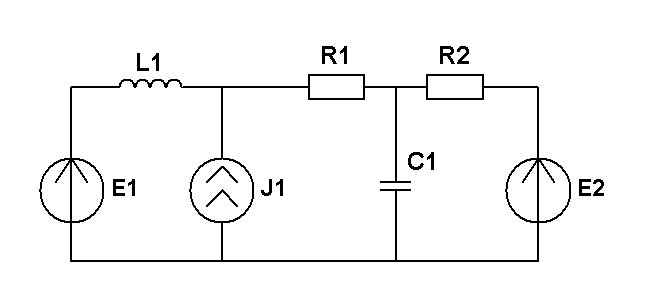
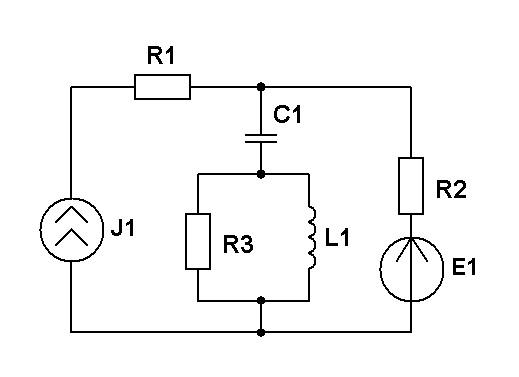
Составить уравнения контурных токов и узловых напряжений и решить их для численных значений: R₁=R₂=R₃= X_C1=200 Ом

X_L1= X_L2=250 Ом

E₁(t)=3cost,В; J ₁(t)=30cost,мА;

E₂(t)=3cost,В;

E₃(t)=5cost, В.;

4

Е ₁=80 В

J=0,4 мА

R₁=R₂=1 кОм

X_C=1 кОм

X_L=2 кОм.

Рассчитать методом наложения ток в сопротивлении R₂.

₁=10 В

₂=20 В

=1 A

R₁= X_L =R₂=10 Ом

R₃=X_C=50 Ом

Методом эквивалентного генератора рассчитать ток в ветви с R₃.

Вариант №3

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

R=1 кОм

L=2 мГн

C=0,5 нФ

=10⁶ рад/с

Определить мгновенное значение всех напряжений, если амплитуда напряжения между точками 1 и 2 равна 10 В, а начальная фаза напряжения равна 0. Построить векторную диаграмму для комплексных амплитуд токов и напряжений

3

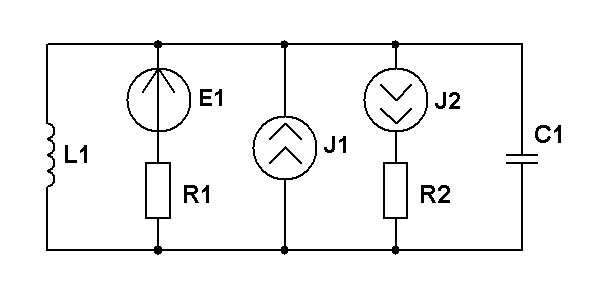
Составить уравнения контурных токов и узловых напряжений и решить их для численных значений:

R1=1 кОм; R₂=100 Ом ;

X_L1=2 кОм; X_C1=3 кОм;

J₁=1 мА; E₁=25 В:

E₂=20 В;

4

R=1 кОм; X_L=2 кОм;

X_C=3 кОм; J₁=1 мА;

J₂=2 мА; J₃=3 мА

Рассчитать методом наложения ток в резисторе.

5

E₁=25 В: E₂=20 В;

R₁=R₂=R₄=X_C=100 Ом;

R₃=25 Ом.

Методом эквивалентного генератора рассчитать ток в ветви с емкостью.

Вариант №4

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=4 кОм

L=8 мГн

C=1 нФ

=10⁶ рад/с

Определить полную мощность, потребляемую цепью, если U_1-2=10 В.

Д

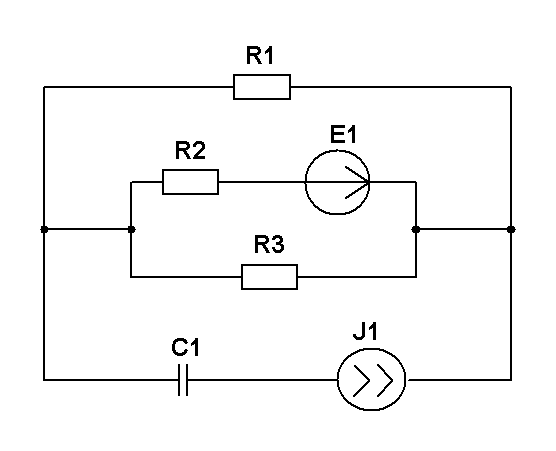
3

напряжений и решить их для численных значений: R₁=R₂=R₃= X_C1=100 Ом;

X_L1= X_L2=25 Ом; ₁=10 В, ₂=20 В, ₁=1 A

4

R₁=1 кОм; J₁=0,4 мА; Е₁ =1 В;

X_C1=3 кОм; X_L1=2 кОм

Рассчитать методом наложения ток в сопротивлении R₁.

5

E₁=10 В; E₂=20е^j90;

J=2е^j45 мA

R₁= 1 кОм

R₂=2 кОм

R₃=5 кОм

X_L1=4 кОм; X_L2 =4 кОм

Методом эквивалентного генератора рассчитать ток в ветви с R₁.

Вариант №5

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R₁=5 кОм; L₁=10 мГн;

C₁=0,1 нФ; =10⁶ рад/с

Определить полную мощность, потребляемую цепью, если U_1-2=1 В. (КДЗ)

3

Для схемы задания 1 составить уравнения контурных токов и узловых

напряжений и решить их для численных значений: R₁=R₂=R₃= X_L1=100 Ом;

X_L2= 25 Ом; ₁=12 В, ₂=18 В, ₁=1 A

4

J₁=1 мА

J₂=0,4 мА

J₃=0,8 мА

R=1 кОм

X_C=3 кОм

X_L=2 кОм

Методом наложения определить ток в индуктивности L.

5

E₁=10 В

E₂=20 В

R₁=R₂=R₄= X_C=100 Ом

R₃= 25 Ом

Методом эквивалентного генератора рассчитать ток в ветви с R₁.

Вариант №6

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=6 Ом

L=12 мГн

C=0,09 нФ

U_1-2=1 В (КДЗ)

=10⁶ рад/с

Определить потребляемую цепью комплексную мощность.

3

Для схемы задания 1 составить уравнения контурных токов и узловых

напряжений и решить их для численных значений: R₁=R₂=R₃= R₄= X_C1=100 Ом;

R₅=X_L1= X_L2= X_C2=25 Ом; ₁=12 В, ₂=18 В, ₁=1 A

R₁=1 кОм

X_C=3 кОм

X_L=2 кОм

e=20cos(t+90) B

J₁=0,4cost, мА

J₂=0,2cost. мА

Методом наложения определить ток в ветви с емкостью С.

5

E₁ =19cos(t+90) B

J₁=0,4cost, мА

R₃=1 кОм

R₂=2 кОм

R₁= 1 кОм

X_C=2 кОм

Методом эквивалентного генератора рассчитать ток в ветви с R₃.

Вариант №7

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=7 кОм

L=4 мГн

C=0,08 нФ

=10⁶ рад/с

Определить мгновенное значение всех напряжений, если U_вх=5 В.

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=12 В, ₂=18 В, ₃=10 В, ₁=0.2 A

4

Е=20 В

J=50 мА

R₁= X_L =1 кОм

R₂=2 кОм

Методом наложения определить ток в ветви с Е.

5

E₁=10 В

J₁=0,1е^j90 A

R₁= 12 Ом; R₂=40 Ом

R₃=10 Ом

X_С =16 Ом;

X_L=60 Ом

Определить методом эквивалентного генератора ток в емкости.

Вариант №8

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=8 кОм

L=16 мГн

C=0,07 нФ

=10⁶ рад/с

Определить мгновенное значение всех напряжений, если U_1-2=10 В. (СКЗ)

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1= X_C2=25 Ом; ₁=12 В, ₁=0.1 A

4

e₁=40cost, B

e₂=5cos(t+90), B

e₃=10cos(t-90), B

X_C=20 Ом

X_L=40 Ом

R=40 Ом

Методом наложения определить ток в индуктивности L.

5

E₁= 50е^j45 В

J₁=10е^j0 мА

J₂=20е^j90 мА

R₁=1 кОм; R₂=200 Ом

X_L1 =100 Ом

X_C1=0,5 кОм

Определить методом эквивалентного генератора ток в ветви с R₂.

Вариант №9

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=3 кОм

L=20 мГн

C=0,5 нФ

=10⁶ рад/с

Определить комплексное сопротивление схемы Z _экв и указать его характер (емкостной, индуктивный или резистивный) на заданной частоте.

3

Для схемы задания 1 составить уравнения контурных токов и узловых

напряжений и решить их для численных значений: R₁=R₂= X_L1 =X_C1= X_C2=100 Ом;

X_L1= 100 Ом; e₁=40cost, B; e₂=10cos(t+90), B; J=0,04cost, А

4

Е₁=125е^j90 В

J=0,1 А

R₁=R₂=60 Ом

X_C=36 Ом

X_L=36 Ом

Методом наложения определить ток в индуктивности L.

5

E₁=25 В

J₁=1 A

R₁= R₂=100 Ом

X_L =25 Ом

X_C=50 Ом

Методом эквивалентного генератора определить ток в R1.

Вариант №10

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=2 кОм

L=2 мГн

C=0,5 нФ

=10⁶ рад/с

U_1-2=1 В

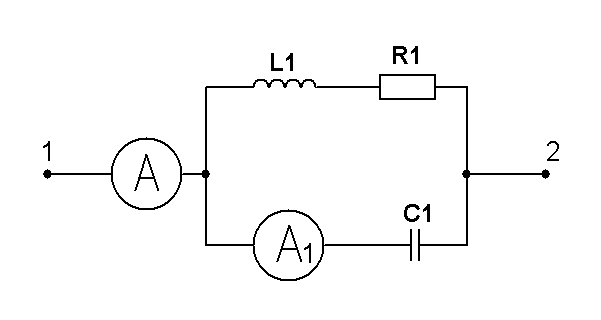
Определить показания приборов.

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=10 В, ₂=20е^j90 В, ₁=0.1 A, ₂=0.1е^j90 A

Е₁=12 В; J₁=0,4 мА

J₂=0,8 мА

R= 1 кОм

X_C=3 кОм

X_L=2 кОм

Методом наложения определить ток в индуктивности L1.

5

, В

,В

j₁=2,82 cos(t+45), А

R₁=10 Ом; R₂=5 Ом

X_L1 =10 Ом; X_С1 =4 Ом

Методом эквивалентного генератора определить ток в ветви с L1.

Вариант №11

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=2 кОм

L=1 мГн

C=0,4 нФ

=10⁶ рад/с

Определить мгновенное значение всех напряжений, если U_1-2=1 В.

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=10 В, ₂=10е^j90 В, ₃=20 B, ₁=0.1е^j90 A

Е₁=20 В

J₁=10 мА

R₁= X_C =1 кОм

R₂=2 кОм

Методом наложения определить ток в ветви с сопротивлением R₂.

5

E₁=10 В

E₂=20е^j90 В

J₁=2,82е^j45 mA

R₁=1 кОм; R₂=2 кОм

R₃=5 кОм

X_L1 =1 кОм; X_L2=4 кОм

Методом эквивалентного генератора определить ток в ветви с L2.

Вариант №12

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=3 кОм

L=3 мГн

C=0,3 нФ

=10⁶ рад/с

U_1-2=10 В.

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=12 В, ₂=20е^j90 В, ₃=10 B, ₄=10е^j90 B.

Е₁=5е^j90, В

Е₂=10е^j90, В

R=100 Ом

X_C=20 Ом

X_L=40 Ом

J₁=2 А

Методом наложения определить ток в ветви с L₁.

5

E =1е^{j90 }, В

J=0,4 мА

R₂= X_L =1 кОм

R₁=1 кОм

X_C=2 кОм

Методом эквивалентного генератора определить ток в R2.

Вариант №13

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=1 кОм

L=1 мГн

C=0,2 нФ

=10⁶ рад/с

U_1-2=12 В

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=12 В, ₂=18е^j90 В, ₁=0.1е^j90 A.

4

Е₁=125 В

J₁=0,1 мА

R₁=R₂=60 Ом

X_C= X_L =36 Ом

Методом наложения определить ток в ветви с сопротивлением R₂.

5

E₁=100 В

J₁=0,1е^j90 A

R₁=12 Ом; R₂=40 Ом

R₃=10 Ом

X_L =60 Ом

X_C=16 Ом

Методом эквивалентного генератора рассчитать ток в ветви с R₂.

Вариант №14

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=5 кОм

L=7 мГн

C=0,4 нФ

=10⁶ рад/с

U_вх=10 В.

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=10 В, ₂=20е^j90 В, ₃=10 B, ₁=0.1е^j90 A.

4

Е₁=12 В

J₁=0,4 мА

J₂=0,8 мА

R=1 кОм

X_C=3 кОм

X_L=2 кОм

Методом наложения определить ток в С.

5

E₁=25 В

J₁=0,2 A

R₁= R₂=R₄=X_L =100 Ом

R₃=25 Ом

Методом эквивалентного генератора определить ток в R2.

Вариант №15

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=6 кОм

L=9 мГн

C=1 нФ

=10⁶ рад/с

U_вх=20 В

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=12 В, ₂=18е^j90 В, ₁=0.1е^j90 A.

4

J₁=1 мА

J₂=0,4 мА

J₃=0,8 мА

R=1 кОм

X_C=3 кОм

X_L=2 кОм

Методом наложения определить ток в С.

5

E₁=25 В

J₁=1 A

R₁= R₂=100 Ом

X_L = 25 Ом

X_C=50 Ом

Методом эквивалент-ного генератора определить ток в С.

Вариант №16

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=2 кОм

L=1 мГн

C=1 нФ

=10⁶ рад/с

U_вх=1 В

Определить активную мощность, потребляемую цепью.

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; ₁=20 В, ₂=10е^j90 В, ₁=0.1е^j90 A.

4

е₁=10cost, В

е₂=10cost, В

i₁=0,01cost, А

R₁=1 кОм

R₂=2 кОм

X_C=3 кОм

X_L=2 кОм

Методом наложения определить ток в R₁.

5

E₁=10 В

E₂=10 В

J₁=1 A

R₁= X_L =R₂=12 Ом

X_C=25 Ом

Методом эквивалентного генератора определить ток в ветви с R₁.

Вариант №17

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=1 кОм

L=1 мГн

C=1 нФ

=10⁶ рад/с

U_вх=10 В

Определить показания приборов.

Д

3

напряжений и решить их для численных значений: R₁=R₂= X_C=100 Ом;

X_L1=25 Ом; X_L2=25 Ом; B, J(t)=200cost, мА

4

Е=10 В

J₁=0,4 мА

J₂=0,8 мА

R=1 кОм

X_C=3 кОм

X_L=2 кОм

Методом наложения определить ток в L.

5

E₁=10 В

E₂=20е^j90 В

J=0.02е^j45 A

R₁=2 кОм

R₂=5 кОм

X_С =1 кОм

X_L=1 кОм

Методом эквивалентного генератора определить ток в С.

Вариант №18

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=10 кОм

L=15 мГн

C=0,08 нФ

=10⁶ рад/с

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений, если U_вх=10В. (СКЗ)

Д

3

напряжений и решить их для численных значений: R₁=R₂= R₃= R₄= X_C=100 Ом;

X_L1=25 Ом; X_L3=25 Ом; E₂=10 В, E₃=20е^j90 В, J=0,2е^j45 A

4

Е=10 В

J₁=1 мА

J₂=0,4 мА

X_C=5 кОм

X_L=2 кОм

Методом наложения определить ток в L.

5

E₁=25 В

E₂=20 В

X_L1=R₁= R₂= 100 Ом

X_С =25 Ом

X_L2=100 Ом

Методом эквивалентного генератора рассчитать ток в ветви с L₁.

Вариант №19

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=1 кОм

L=1 мГн

C=0,5 нФ

=10⁶ рад/с

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений, если U_вх=10В. (СКЗ)

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; е₂=10cost, В , е₃=20cost, В, i₁=100cost, мА

4

Е=10 В

J₁=1 мА

J₂=0,5 мА

X_C=2 кОм

X_L=3 кОм

Методом наложения определить ток в L.

5

E=100 В

J=0,1е^j90 A

R₁= 12 Ом

R₂=40 Ом

R₃=10 Ом

X_C=16 Ом

Методом эквивалентного генератора рассчитать ток в ветви с R₂.

Вариант №20

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа)

2

R=5 кОм

L=10 мГн

C=0,01 нФ

=10⁶ рад/с

U_вх=1 В

Определить амплитуды всех токов.

Д

3

напряжений и решить их для численных значений: R= X_C=100 Ом;

X_L=25 Ом; е₁(t)=10cost, В , е₂(t)=20cost, В, J₁(t)=J₂(t)=100cost, мА

4

Е=20 В

J=20 мА

R₁=2 кОм

R₂= X_C =1 кОм

Методом наложения определить ток в ветви с сопротивлением R₁.

5

E₁=30 В

E₂=15 В

J=0,5 A

R= X_L =1 кОм

X_C=2 кОм

Методом эквивалентного генератора рассчитать ток в L.

Вариант №21

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа

2

R=1 кОм

L=1 мГн

C=0,5 нФ

=10⁶ рад/с

U_вх=10 В

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Д

3

напряжений и решить их для численных значений: R₁=R₂= R₃= X_C=100 Ом;

X_L=25 Ом; е₁(t)=10cost, В , е₂(t)=20cost, В, J(t)=100cost, мА

4

Е₁=5е^j0 В

Е₂=10е^j90 В

J1=0,02е^j90 А

R1=R2=R3=1 кОм

X_L1= X_L2=2 кОм

Методом наложения определить ток в ветви с сопротивлением R1.

5

E₁=10В

E₂=20е^j90 В

J=20 мA

R₁=1 кОм; R₂=2 кОм

X_C=4 кОм; X_L=1 кОм

Методом эквивалент-ного генератора рассчитать ток в L.

Вариант №22

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа

2

R=3 кОм

L=2 мГн

C=0,4 нФ

=10⁶ рад/с

U_вх=1 В

Определить сдвиг фаз между напряжением и током на входе.

Д

3

напряжений и решить их для численных значений: R₁=R₂= R₃= X_C=100 Ом;

X_L1=25 Ом; X_L2=25 Ом; е₁(t)=10cost, В , е₂(t)=20cost, В, J(t)=100cost, мА

4

Е=25 В

J=1 А

R₁=50 Ом

R₂= X_C =100 Ом

X_L=25 Ом

Методом наложения определить ток в C.

5

E₁=25 В; E₂=20 В

R₁= R₂=100 Ом

R₃=25 Ом

R₄=50 Ом

X_C=100 Ом

X_L =100 Ом

Определить методом эквивалентного генератора напряжений ток на закороченном участке 3-4.

Вариант №23

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа

2

R=4 кОм

L=3 мГн

C=0,3 нФ

=10⁶ рад/с

U_вх=10 В

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L=25 Ом; е₁(t )=10cost, В , е₂(t) =20cost, В, J(t) =100cost, мА

4

Е₁=20 В; J=0,1 А

R₁=100 Ом

R₂=20 Ом

R₃=50 Ом

X_C=100 Ом

Методом наложения определить ток в ветви с сопротивлением R₂

5

E₁=25 В

E₂=20 В

R₁= X_L =R₂=R₄=100 Ом

R₃= 25 Ом

Методом эквивалентного генератора рассчитать ток в L.

Вариант №24

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа

2

R=5 кОм

L=4 мГн

C=0,25 нФ

=10⁶ рад/с

U_вх=10В.

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L1=25 Ом; X_L2=25 Ом; X_c1=25 Ом; е(t )=10cost, В , е₁(t) =20cost, В, J(t) =100cost, мА

4

Е=20 В

J=8 мА

R= X_L =1 кОм

X_C=2 кОм

Методом наложения определить ток в С.

5

E=10 В

J=0,1е^j90 A

R₁= 12 Ом

R₂=40 Ом

R₃=10 Ом

X_C=16 Ом

X_L=16 Ом

Методом эквивалентного генератора рассчитать ток в ветви с R₂.

Вариант №25

1

Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. (уравнения по 1 и 2 закону Кирхгофа

2

R=6 кОм

L=5 мГн

C=0,2 нФ

=10⁶ рад/с

U_вх=10 В

Определить мгновенные значения всех токов и напряжений и построить векторную диаграмму для комплексных амплитуд токов и напряжений

Для схемы задания 1 составить уравнения контурных токов и узловых

3

X_L=25 Ом; е₁(t )=10cost, В , е₂(t) =20cost, е₃(t) =20cost, В, J(t) =100cost, мА

4

J₁=1 мА

J₂=0,8 мА

R=1 кОм

X_C= X_L =2 кОм

Методом наложения определить ток в ветви с L.

5

E₁=10В

E₂=20е^j90 В

J=2е^j45 мA

R₁=1 кОм

R₂=2 кОм

R₃=5 кОм

X_C=0,5 кОм

Методом эквивалентного генератора рассчитать ток в ветви с R₁.