Пример реализации фильтра Баттерворта 3го порядка

Аналоговый прототип Фильтра Баттерворта 3^го порядка имеет квадрат модуля комплексного коэффициента передачи:

|H(jΩ)|² = = H(jΩ)·H(-jΩ) (1)

Произведение операторного коэффициента передачи H(S) на зеркальную функцию H(-S) будет иметь вид:

H(S) H(-S) = 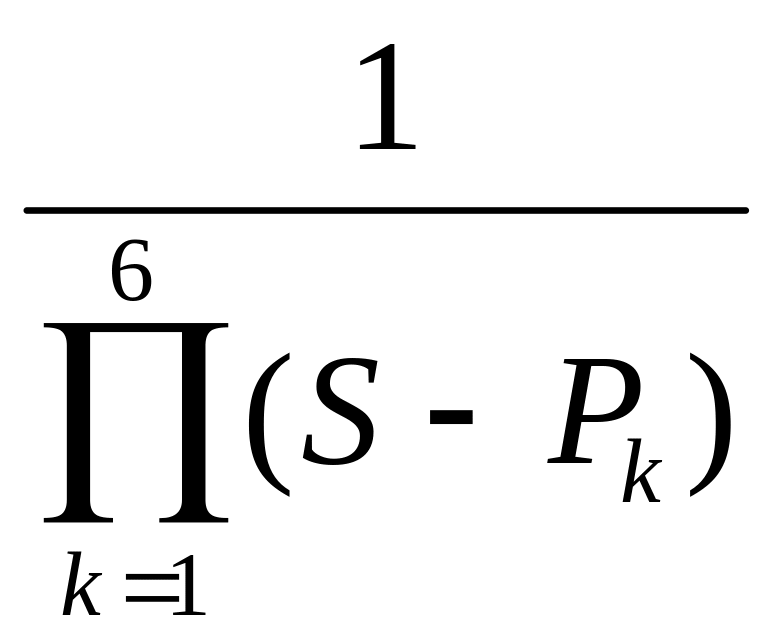(2)

P_k=jΩ_k=je^j , k= 1,2,3,4,5,6

К

+jω

орни P_k для этого фильтра на комплексной плоскости расположены на окружности единичного радиуса:

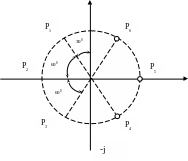
Рисунок 1 – Расположение полюсов аналогового фильтра

на комплексной плоскости

Первые три полюса P₁, P₂, P₃ расположены в левой полуплоскости. В соответствии с условиями физической реализуемости, они принадлежат передаточной функции H(p).

Полюса P₄, P₅, P₆ расположены в правой полуплоскости и принадлежат зеркальной функции H(-P).

Следовательно:

H(S)= 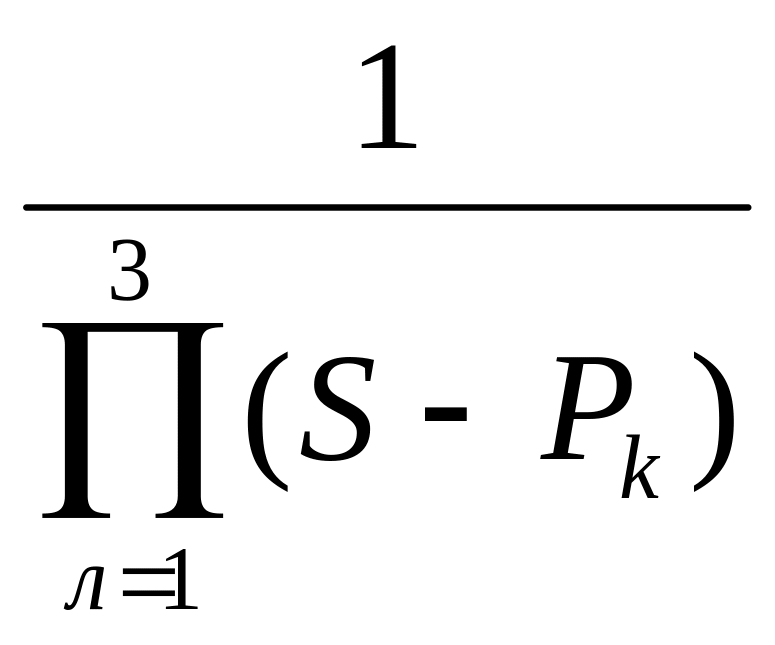, (3)

где P₁=- ;

P₂=-1;

P₃=-

Подставим значения, получим формулу для операторного коэффициента передачи в следующем виде:

H(S)=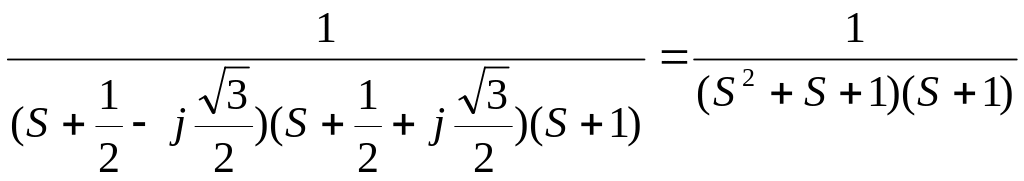 (4)

Используем билинейное преобразование для перехода от операторного коэффициента передачи к Z-преобразованию функции передачи фильтра:

P=2f_g (5)

где f_g – частота дискретизации.

Пусть частота среза фильтра определяется равенством:

f_c=0,2 f_g (6)

S=jΩ=j =j =j (7)

S= (8)

на частоте функция передачи будет иметь вид:

H(P)= = 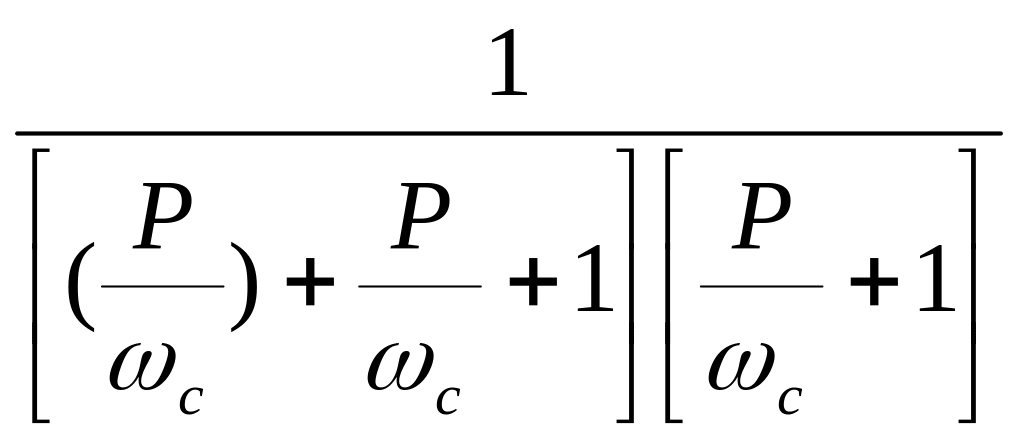(9)

Подставив в (9) (5) и (6) получим:

H_(Z)= (10)

X=

После упрощения (10) будет иметь вид:

H_(Z)=

Этой функции соответствует структурная схема рисунок 2.

X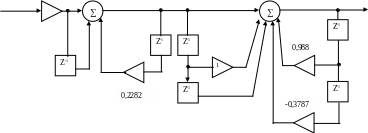 _(k) Y_(k)

Рисунок 2 – Структурная схема цифрового фильтра

Баттерворта 3^го порядка с f_c=02fg

Проверим с помощью пакета MATLAB 6.5, что эта структурная схема действительно соответствует фильтру Баттерворта.

>> в = [ ] % вектор коэффициентов числителя Z - преобразования функции передачи;

>> а = [ ] % вектор коэффициента знаменателя той же функции;

>> f gz(в,а).

Пример:

Фильтр Баттерворта 3^го порядка с частотой среза f_c=0,2fg или f_N= , f_c=0,4f_N,

где f_c – частота среза ФНЧ (граница ПП);

f_g = - частота дискретизации;

f_N – частота Нейквиста

имеет Z-преобразование передаточной функции, полученное с помощью билинейного преобразования:

H_(Z)= =

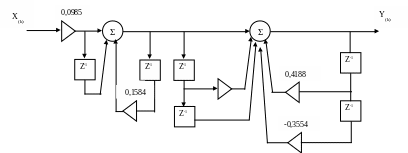
При расчете по этому оператору по умолчанию используются нормированные значения частот, измеряемые в радианах на отсчет. При такой нормировке частота дискретизации равна 2π, а частота Найквиста (максимальная частота спектра сообщения) равна π. При этом число частотных точек равно 512 на интервале 0/π с постоянным частотным шагом. [с. 218, 1]

3.2. Варианты заданий Вариант 1 Дискретная цепь описывается разностным уравнением

y[n]=x[n]-0,5x[n-1]+1,0x[n-2]-1,5x[n-3].

1. Записать передаточную функцию H(Z) цепи.

2. Записать АЧХ |H(j)| цепи.

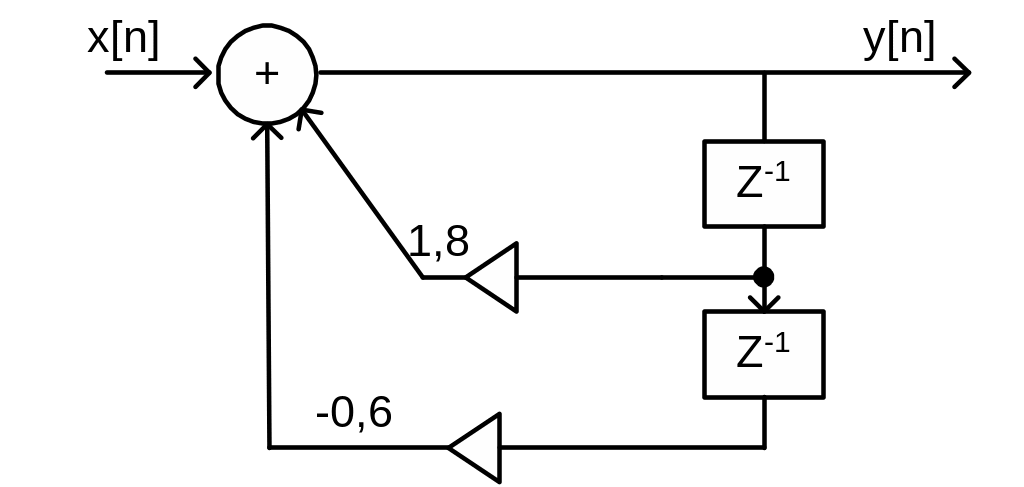
3. Привести схему дискретной цепи.

4. Определить отсчеты дискретной импульсной характеристики h[n] цепи.

5. Используя уравнение дискретной свертки, рассчитать отсчеты реакции y[n] цепи на воздействие x[n]=[1; 2; 0; -1].

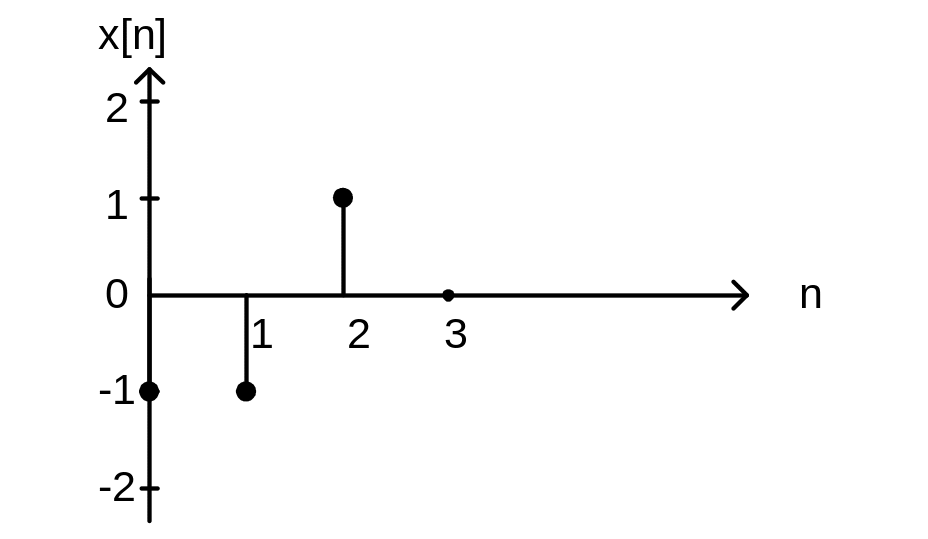Вариант 2

1. Записать передаточную функцию H(Z) цепи.

2. Записать АЧХ |H(j)| цепи.

3. Записать разностное уравнение дискретной цепи.

4. Получить формулу и рассчитать отсчеты дискретной импульсной характеристики h[n] цепи.

5. Рассчитать отсчеты реакции y[n] цепи на воздействие x[n].

Вариант 3