Амплитудно-частотная характеристика линейной дискретной системы

Для согласованного z-преобразования комплексная переменная «z» и «p» связаны уравнением (18):

Z=e^pTg

Преобразованию Лапласа можно сопоставить преобразование Фурье (там, где это допустимо). Если в преобразовании Лапласа сделать замену переменной p=jω, то тем самым из преобразования Лапласа будет получено для определенного класса непрерывных функций времени преобразования Фурье.

При замене

(55)

В формуле для z-преобразования функции передачи ЛДС (48) можно получить комплексный коэффициент передачи линейной дискретной системы:

(56)

Определение:

Амплитудно-частотной характеристикой ЛДС называется модуль комплексного коэффициента передачи линейной дискретной системы т.е.:

(57)

с учетом (46)

(58)

Комплексная частотная характеристика и амплитудно-частотная характеристика ЛДС при билинейном преобразовании

При билинейном преобразовании комплексная переменная «p» и комплексная переменная «z» связаны уравнениями (31), (32).

Для непрерывной линейной системы (линейной цепи) можно записать операторный коэффициент передачи как отношение изображения отклика цепи к изображению входного воздействия при нулевых начальных условиях:

, (59)

где

,

Для физически реализуемой цепи знаменатель операторной функции передачи H(p) является полиномом Гурвица.

Для перехода к z-преобразованию функции передачи можно сделать подстановку в H(p) вместо «p» из (31):

,

затем получившуюся функцию записать как отношение полиномов степеней (z^-1). При записи уравнений для фильтров, предполагается, что предварительно получена передаточная функция денормированного по частоте аналогового фильтра [2].

Для нахождения комплексной частотной характеристики, так же как при согласованном z-преобразовании делают подстановку:

(60)

где ω_y - цифровая частота;

учитывая, что p=jω_a,

где ω_a - аналоговая частота.

Связь между осью частот дискретной и аналоговой цепи становится комплексной:

(61)

отсюда

(62)

Однако (62) позволяет устранить деформацию частотной шкалы, путем пересчета граничных частот аналогового фильтра [2].

Примеры расчета характеристик дискретных цепей (тестовых заданий)

Пример 1

Задано разностное уравнение:

y(n)=a₀x_(n)+a₁x_(n-1)+a₂x_(n-2)+a₃x_(n-3) (63)

1 Записать передаточную функцию H(z) цепи.

Для уравнения (63) найдем его z-преобразование:

Y(z)=a₀z_(z)+a₁z^-1x_(z)+a₂z^-2x_(z)+a₃z^-3x_(z) (64)

По определению, z – преобразование функции передачи равно отношению z – преобразования отклика цепи Y(z) к z – преобразованию входного воздействия x_(z):

(65)

2 Записать АЧХ дискретной цепи (63), полагая a₀=a₁=a₂=a₃=1.

Пусть входная последовательность представляет собой отсчеты комплексной экспоненты:

(66)

Выходная последовательность y_(n) равна дискретной свертке входной последовательности x_(n) и дискретной импульсной характеристики ЛДС h_(n):

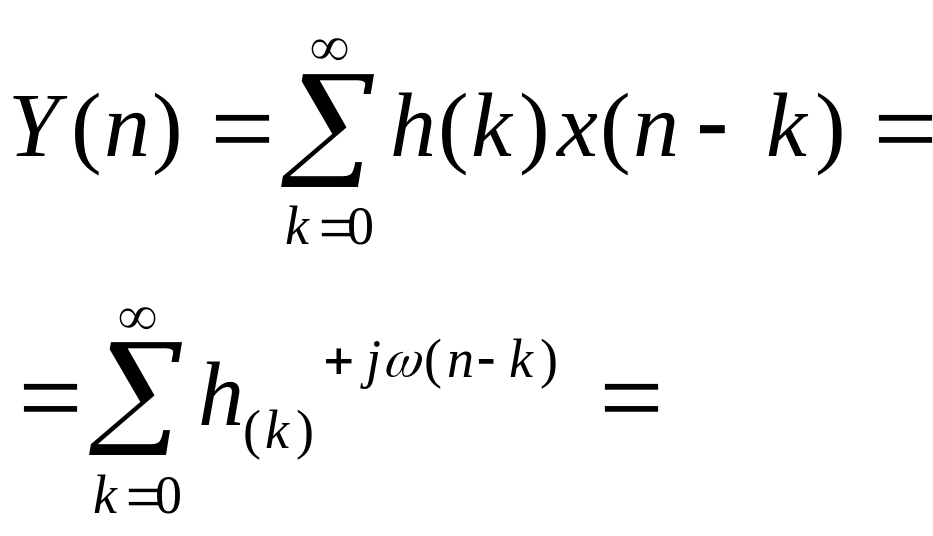
= (67)

Здесь H( ) – комплексная частотная характеристика дискретной цепи.

(68)

Допустим, что входной сигнал – отсчеты гармонической функции амплитуды A, частоты ω₀, начальной фазы :

(69)

(70)

(71)

Выходной сигнал y₁(n) на x₁(n) равен:

(72)

Выходной сигнал y₂(n) на x₂(n) равен:

(73)

Отсчеты выходной последовательности y(n) равны сумме y₁(n) и y₂(n)

(74)

Учитывая, что и - комплексно-сопряженные функции, можно записать:

(75)

Пусть - частота Найквиста

- интервал дискретизации, выбранный в соответствии с теоремой Котельникова для сигнала с ограниченным спектром.

(76)

где - круговая частота дискретизации.

Обозначим нормированную частоту

произведение:

(77)

Выразим из (75) Tg и подставим (77):

(78)

Определим комплексную частотную характеристику ЛДС как функцию частоты :

(79)

Для разностного уровня (63) при заданных исходных данных комплексная частотная характеристика дискретной цепи равна

(80)

где h(n) – дискретная импульсная характеристика.

(81)

h(n)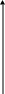

1

n

0

1

2

3

Рисунок 3 – График дискретной импульсной

характеристики ЛДС, N =4

(82)

Формула (82) получена на основе вычисления суммы геометрической прогрессии.

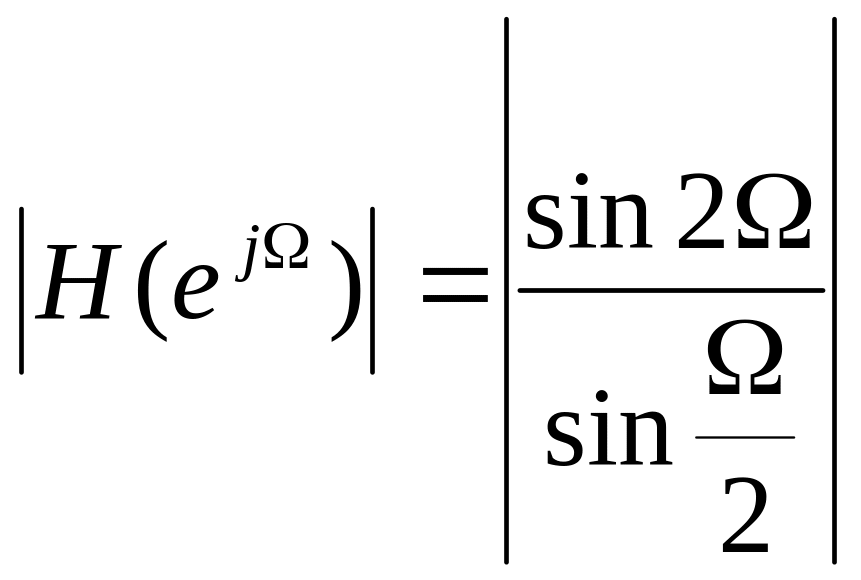
Ω

Р исунок 4 – График АЧХ ЛДС (пример 2)