
- •1.Матричный метод расчета хтс
- •2.Декомпозиционный метод расчета сложных хтс
- •2.1 Выделение контуров
- •2.2 Определение Оптимально-разрывающего множества дуг (омрд)
- •2.3 Определение окончательной последовательности расчета хтс
- •3.Расчет хтс с помощью моделирующей программы (м92).
- •3.1 Математическое описание элементов хтс
С
1
2
3
4
7
6
5
9
8
10
500
кг/ч
500
кг/ч
рисунок 1.
















Задачей курсового проекта было вычисление потоков представленных на рисунке 1.
В курсовой работе будет представлены следующие способы вычисления потоков:
1) Матричный метод расчета ХТС.
2) Декомпозиционный метод расчета ХТС.
3) Программная обработка на М92.
4) Итерационный способ расчета ХТС.
1.Матричный метод расчета хтс
Заданные уравнения связи между параметрами входных и выходных потоков аппаратов имеют линейный вид. Уравнения материального баланса для каждого аппарата и дополнительные уравнения связи между потоками:
G21 – G15 = 0
G26 + G21 = 500
G34 + G36 –G93 =500
G34 + G94 – G47 = 0
G15 – G56 – G58 = 0
G26 + G36 + G56 – G68 – G69 = 0
G47 – G79 = 0
G58 + G68 + G108 – G810 = 0
G69 + G79 – G93 – G94 – G910 = 0
G810 + G109 – G108 –G100 = 0
G21 = 250
G34 – 0.5*G93 = 0
G56 – 0.5*G15 = 0
G68 – 0.5*G26 – 0.5*G36 – 0.5*G56 = 0
G93 – 0.3*G69 – 0.3*G79 =0
G94 – 0.4*G69 –0.4*G79 = 0
G108 – 0.5*G810 –0.5*G910 = 0
Для решения системы (1) ее следует привести к стандартному виду систем линейных алгебраических уравнений:
a11х1+a12х2+…..+a1nхn=bi
……. (2)
an1х1+an2х2+…..+annхn=bn
Здесь n-число уравнений и аргументов; хj-аргументы системы уравнений, в качестве которых в уравнениях (1) рассматриваются неизвестные расходы;
aij-коэффициенты системы линейных уравнений; bi-свободные члены, не содержащие неизвестных параметров.
Удобно результат преобразования системы (1) к стандартному виду (2) представить в табличной (матричной, А) форме. Номер строки соответствует порядковому номеру уравнения, а номер столбца - номеру аргумента, тогда матрица коэффициентов при неизвестных расходах и вектор правых частей (свободных членов bi, B) примет вид, приведенный в таблице

Т
Столбец
свободных членов аблица
1.
аблица
1.
№ Ур |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
g15 |
g21 |
g26 |
g34 |
g36 |
g47 |
g56 |
g58 |
g68 |
g69 |
g79 |
g93 |
g94 |
g910 |
g810 |
g108 |
g100 |
В |
|
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
G02 |
3 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
500 |
G03 |
4 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-1 |
-1 |
0 |
|
11 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
250 |
0,5G02 |
12 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-0,5 |
0 |
0 |
0 |
0 |
0 |
250 |
0,5G03 |
13 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
14 |
0 |
0 |
-0,5 |
0 |
-0,5 |
0 |
-0,5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-0,3 |
-0,3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-0,4 |
-0,4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-0,5 |
-0,5 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
250 |
g15 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
250 |
g21 |
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
250 |
g26 |
4 |
-0 |
0,2 |
0,2 |
-0,4 |
0 |
-0,4 |
-0,4 |
0 |
0 |
0 |
-0,1 |
1,2 |
0,2 |
-0,4 |
0,8 |
0,4 |
0 |
475 |
g34 |
5 |
-0 |
0,2 |
1,2 |
-0,4 |
0 |
-0,4 |
-0,4 |
0 |
0 |
0 |
-0,1 |
-0,8 |
0,2 |
-0,4 |
0,8 |
0,4 |
0 |
475 |
g36 |
6 |
-0 |
0,733 |
0,7333 |
-2,47 |
0 |
-1,467 |
-1,467 |
0 |
0 |
0 |
-0,37 |
1,7333 |
0,733 |
-1,5 |
1,6 |
2,47 |
0 |
1075 |
g47 |
7 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0 |
1 |
0 |
0 |
0 |
0 |
125 |
g56 |
8 |
-1 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0 |
-1 |
0 |
0 |
0 |
0 |
125 |
g58 |
9 |
-0 |
0,6 |
0,6 |
-0,2 |
0 |
-0,2 |
-0,2 |
0 |
0 |
0 |
-0,3 |
-0,4 |
0,6 |
0,8 |
0,4 |
0,2 |
0 |
425 |
g68 |
10 |
-0 |
0,6 |
0,6 |
-0,2 |
0 |
-1,2 |
-0,2 |
0 |
0 |
0 |
-0,3 |
-0,4 |
0,6 |
-1,2 |
0,4 |
0,2 |
0 |
425 |
g69 |
11 |
-0 |
0,733 |
0,7333 |
-2,47 |
0 |
-1,467 |
-2,467 |
0 |
0 |
0 |
-0,37 |
1,7333 |
0,733 |
-1,5 |
1,6 |
2,47 |
0 |
1075 |
g79 |
12 |
-0 |
0,4 |
0,4 |
-0,8 |
0 |
-0,8 |
-0,8 |
0 |
0 |
0 |
-0,2 |
0,4 |
0,4 |
-0,8 |
1,6 |
0,8 |
0 |
450 |
g93 |
13 |
-0 |
0,533 |
0,5333 |
-1,07 |
0 |
-1,067 |
-1,067 |
0 |
0 |
0 |
-0,27 |
0,5333 |
0,533 |
-1,1 |
0,8 |
2,07 |
0 |
600 |
g94 |
14 |
-0 |
0,4 |
0,4 |
-0,8 |
0 |
-0,8 |
-0,8 |
0 |
-1 |
0 |
-0,2 |
0,4 |
0,4 |
-0,8 |
-0,4 |
-0,2 |
0 |
450 |
g910 |
15 |
-2 |
1,6 |
1,6 |
-1,2 |
-2 |
-1,2 |
-1,2 |
-2 |
-1 |
-2 |
0,2 |
-0,4 |
-0,4 |
0,8 |
0,4 |
0,2 |
-2 |
1550 |
g810 |
16 |
-1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-2 |
0 |
0 |
0 |
0 |
0 |
0 |
-2 |
1000 |
g108 |
17 |
-1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
g100 |

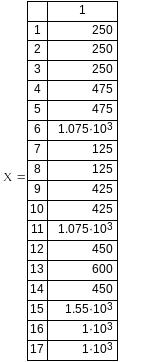
Решение системы уравнений
Решение системы уравнений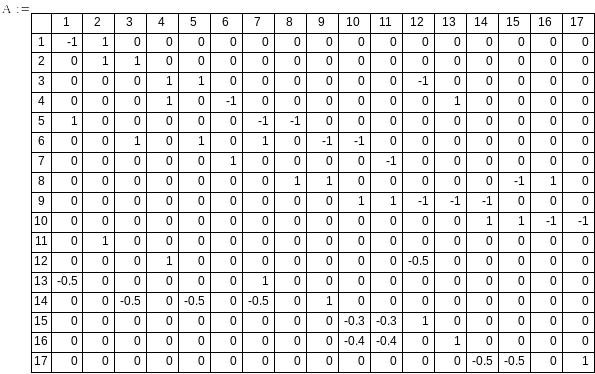
![]()

![]()
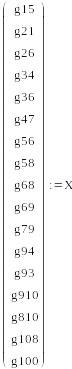

 000
000