Глава 3. Плоскопараллельное движение твердого тела
§ 3.1. Общие понятия и определения
3.1. Плоскопараллельным или плоским называется такое движение твердого тела, при котором каждая его точка движется в плоскости, параллельной некоторой фиксированной плоскости п (рис. 3.1).
Уравнение плоскопараллельного движения твердого тела
При
плоскопараллельном движении рис. 3.1
любое сечение тела
,
параллельное плоскости П,
должно оставаться параллельным плоскости
П
в процессе всего движения. В сечение
выберем произвольную точку
и проведем
через неё прямую, перпендикулярную к
плоскостям
и П.
В процессе плоскопараллельного движения
тела эта прямая остается параллельной
самой себе, следовательно, она движется
поступательно. Тогда все точки тела,
лежащие на этой прямой, например,
будут иметь одинаковые скорости,
ускорения и траектории. Следовательно,
достаточно знать движение точки
в сечения
,
чтобы знать движение любой точки тела,
лежащей на рассматриваемой прямой.
Аналогично можно взять любую другую
точку сечения
,
например, точку
и получить тот же вывод. Отсюда следует,
что плоскопараллельное движение тела
будет известно, если будет известно
движение фигуры
.
Вывод: Изучение плоскопараллельного движения твердого тела сводится к изучению движения произвольного сечения тела, параллельного плоскости П.
Движение
любой плоской фигуры
в неподвижной системе координат
на плоскости, при известных форме и
размерах фигуры
,
определяется по движению произвольного
отрезка
известной длины и ориентации по отношению
к фигуре (рис.3.2).
Точку А
на Ф
назовем полюсом, второй конец отрезка
обозначим точкой
.
Положение отрезка
на плоскости (следовательно, и положение
фигуры) будет в каждый момент времени
определено, если знать координаты полюса
и угол
,
который отрезок
образует с осью
.
Положение точки
можно определить по известной длине
отрезка
.
Рис.3.3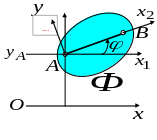
С
фигурой свяжем две системы координат
и
.
Оси
и
в процессе
движения остаются параллельными
неподвижным осям
,
т.е. оси системы координат
при движении фигуры Ф
движутся
поступательно. Движение фигуры Ф
в системе координат
есть движение вращательное относительно
подвижной оси
,
проходящей через точку
перпендикулярно плоскости чертежа (на
рисунке не показана). Система координат
жестко
связана с фигурой и движется вместе с
ней. Если фигура Ф
в процессе движения поворачивается, то
повернется и система координат
.
Поворот фигуры, происходящий в процессе
ее движения относительно точки
,
можно теперь определить углом поворота
между осями
и
(рис.3.2) или, что то же самое, между осями
и
.
Окончательно, движение отрезка
определяется уравнениями:
,
,
(3.1)
Эти же уравнения определяют движение плоской фигуры Ф, а по движению фигуры Ф определяется движение и самого тела.