Движение точки в плоскости.

Если точка M движется оставаясь в некоторой плоскости, то соответствующие формулы (1.30)- (1.41) упрощаются. Связав с этой плоскостью систему координат Оxy, будем иметь:

(1.43)

(1.44)

(1.45)

(1.46)

(1.47)

(1.48)

Вектор скорости , его проекции на оси координат и углы α₁, β₁, образованные с осями координат, для случая, когда точка движется в плоскости, показаны на рис.1.7а.

Вектор ускорения , его проекции и углы α₂, β₂, образованные с осями координат для случая, когда точка движется в плоскости, показаны на рис.1.7б. На рис.1.7а и 1.7б построения векторов выполнены так, чтобы выполнялись равенства: ,

Проекции векторов скорости и ускорения на оси координат - величины суть алгебраические. По модулю проекции вектора скорости , например, можно судить о скорости перемещения точки вдоль оси Ох. По знаку этой проекции можно судить о направлении перемещения ( если , то точка движется в положительном направлении оси Ох, если , то точка движется в обратную сторону).

1.22. Проекции вектора скорости являются алгебраическими величинами скоростей точки в направлении соответствующих осей.

По проекциям вектора ускорения определяется вектор ускорения и характер движения (ускоренное или замедленное).

Если , то точка вдоль оси движется ускоренно. При этом, если , то точка движется в положительном направлении оси Ох, если , то точка движется в обратную сторону.

Если (проекции векторов скорости и ускорения точки имеют разные знаки), то точка направлении оси Ох движется замедленно (модуль проекци убывает). При этом, если , то точка движется в положительном направлении оси Ох, если , то точка движется в обратную сторону.

Прямолинейное движение точки вдоль одной оси

Итак, пусть траектория точки - прямая линия. Выберем на этой прямой произвольную точку и примем её за начало одномерной системы координат Ох. В этой системе координат положение точки будет определяться только одой координатой . Все соотношения упрощаются, и мы будем иметь:

, = . (1.49)

, , (1.50)

В этом случае отпадает необходимость в индексах, так как ось одна единственная. Проекции векторов скорости и ускорения , .

Пример 1.4. Покажем некоторые возможные варианты прямолинейного движения точки.

1) На рис.1 показано ускоренное прямолинейное движение точки по правой полуоси ( ) в положительном направлении оси координат.

2) На рис. 2 показано прямолинейное замедленное движение по правой полуоси в положительном направлении оси координат. Точка, находясь правее начала координат, движется в положительном

Рис. к примеру 1.4.-1. Ускоренное движение точки вправо

направлении оси координат замедленно ( как бы стремиться к покою). Но это не означает, что точка в следеющий момент времени остановиться – есть только тенденця к «останову», проявивщаяся только в данный, показанный на рисунке, момент времени.

Рис. к примеру 1.4.-2. Замедленное движение точки вправо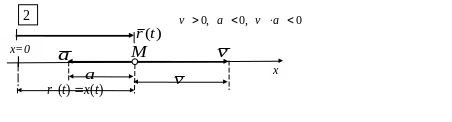

3) На рис. 3 показано прямолинейное ускоренное движение по правой полуоси в отрицательном направлении оси координат. Точка движется к началу координат. При этом . Точка находится справа от начала координат, движется к началу координат.

3

4) На рис.4 показано прямолинейное ускоренное движение по левой полуоси ( ) в отрицательном направлении оси координат. Точка движется от начала координат в отрицательном направлении - влево.

Другие возможные ситуации, возникающие при прямолинейном движении точки, предлагается рассмотреть самостоятельно.