
- •Глава 1. Кинематика точки
- •§ 1.1. Основные понятия и определения. Задачи кинематики
- •1.1. Раздел механики, в котором изучается механическое движение точек и тел без учета их массы и действующих на них сил, называется кинематикой.
- •1.2. Материальные частицы бесконечно малых размеров, из которых состоят абсолютно твердые тела, называются в механике материальными точками.
- •1.3. Механическим движением точки или твердого тела называется изменение с течением времени положения точки или тела в пространстве по отношению к другому телу.
- •1.4. Тело отсчета и неизменно связанная с ним система координат образуют систему отсчета.
- •§ 1.2. Векторный способ задания движения
- •1.10. При векторном способе задания движения траекторией движения точки является годограф радиус-вектора .
- •§ 1.3. Вектор перемещения, вектор скорости и вектор ускорения точки
- •1.11. Движение точки называется прямолинейным, если она движется по прямолинейной траектории.
- •Вектор скорости точки в данный момент времени.
- •1.16. Вектором среднего ускорения точки за промежуток времени называется отношение приращение вектора скорости, произошедшее за данный промежуток времени, к самому промежутку времени.
- •§ 1.4. Координатный способ задания движения
- •1.19. Уравнения (1.17) называются уравнениями движения точки при координатном способе задания движения в декартовой прямоугольной системе координат.
- •Уравнение траектории при координатном способе задания движения
- •1.120. Чтобы определить уравнение траектории точки в заданной системе отсчета, при координатном способе задания движения необходимо исключить время t в уравнениях движения.
- •§ 1.4. Связь между координатным и векторным способами задания движения
- •2. Точка движется в трехмерном пространстве
- •§ 1.5. Скорость и ускорение точки при координатном способе задания движения
- •1.20. Проекции вектора скорости равны первым производным по времени от соответствующих функций закона движения точки (1.7).
- •Движение точки в плоскости.
- •1.22. Проекции вектора скорости являются алгебраическими величинами скоростей точки в направлении соответствующих осей.
- •Прямолинейное движение точки вдоль одной оси
- •§ 1.6. Задачи с решениями на исследование движения точки при векторном и координатном способах задания движения.
- •§ 1.6. Естественный способ задания движения точки
- •1.23. Чтобы задать движение точки естественным способом необходимо произвести следующие действия:
- •1) На траектории точки выбрать начало координат о1 и ввести криволинейную систему координат о1s так, чтобы ось о1s полностью совпала с траекторией.
- •Алгебраическое значение скорости (понятие вводится при естественном способе задания движения)
- •1.25. Алгебраическое значение скорости точки в данный момент времени равно первой производной по времени от функции s(t).
- •Ускорения при естественном способе задания движения
- •1.28. Движение точки м по траектории будет ускоренным, если векторы и направлены по касательной к траектории в одну сторону, и движение точки будет замедленным в противном случае.
- •1.29. Движение точки м по траектории будет ускоренным, если произведение , и движение точки по траектории будет замедленны, если .
- •§ 1.7. Связь между координатным и естественным способами задания движения
- •§ 1.8. Законы равномерного и равнопеременного движений точки
- •Прямолинейное равномерное движение точки.
- •Равнопеременное прямолинейное движение точки.
- •3. Равномерное криволинейное движение точки.
- •Равнопеременное криволинейное движение точки.
- •1.26 Если при движении точки , то движение будет ускоренным. В этом случае вектор скорости и вектор касательного ускорения направлены в одну сторону (сонаправлены) и модуль скорости возрастает.
- •§ 1.9. Свободное прямолинейное движение точки по
- •§ 1.10. Задачи по кинематике точки для самостоятельного решения
2. Точка движется в трехмерном пространстве
![]() .
(1.23)
.
(1.23)
![]() ,
(1.24)
,
(1.24)
,
,
![]() ,
(1.25)
,
(1.25)
![]() (1.26)
(1.26)
Обратная задача. Здесь заданным или известным принимается радиус-вектор точки . По заданному (известному) радиус-вектору нужно построить функции типа (1.17), которые определяли бы движение точки координатным способом. Выкладки проведем только для движения точки в пространстве. Для движения в плоскости надо будет просто пробросить (обнулить) функции с индексом « z ».
а) Радиус - вектор
задан своими координатами
![]() .
.
![]() (1.27)
(1.27)
Тогда
![]()
![]() ,
,
![]()
![]() ,
,
![]() =
=![]() .
(1.28)
.
(1.28)
б) Радиус - вектор
задан модулем
и направляющими косинусами углов
![]() ,
,
![]() ,
,
![]() .
Тогда (рис.1.6) получим:
.
Тогда (рис.1.6) получим:
![]() ,
,
,
,
![]() (1.29)
(1.29)
То есть движение определилось координатным способом.
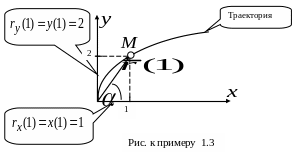
Пример 1.3. Движение
точки в плоскости
![]() задано векторным способом
задано векторным способом
![]() .
Задать это движения координатным
способом. Изобразить уравнение траектории
точки и показать на рисунке данный
радиус – вектор в момент времени
.
Задать это движения координатным
способом. Изобразить уравнение траектории
точки и показать на рисунке данный
радиус – вектор в момент времени
![]()

Р





 ешение.
Радиус вектор точки задан
через свои проекции
ешение.
Радиус вектор точки задан
через свои проекции
![]() .
.
![]()
![]() .
Таким образом, при координатном способе
движение задается уравнениями
.
Таким образом, при координатном способе
движение задается уравнениями
![]()
![]() .
Получим уравнение траектории. Из
второго уравнения движения выразим
время:
.
Получим уравнение траектории. Из
второго уравнения движения выразим
время:
![]() .
Подставим это
в
первое уравнение движения. Тогда получим
следующее уравнение траектории:
.
Подставим это
в
первое уравнение движения. Тогда получим
следующее уравнение траектории:
![]() .
Это верхняя часть параболы (так как
уравнения движения дают
.
Это верхняя часть параболы (так как
уравнения движения дают
![]() )
с ветвями вытянутыми вдоль оси
)
с ветвями вытянутыми вдоль оси
![]() .
При
.
При
![]() точка имеет координаты
точка имеет координаты
![]() .
Эти же значения определяют значения
проекций радиус-вектора
для момента времени
.
Эти же значения определяют значения
проекций радиус-вектора
для момента времени
![]() .
По вычисленным значениям проекций
радиус - вектора
.
По вычисленным значениям проекций
радиус - вектора
![]() строится сам вектор для
конкретных моментов времени, как показано
на рисунке. Тангенс угла наклона
строится сам вектор для
конкретных моментов времени, как показано
на рисунке. Тангенс угла наклона
![]() радиус-вектора к оси
равен:
радиус-вектора к оси
равен:
![]() .
Угол
теперь можно найти по таблицам.
.
Угол
теперь можно найти по таблицам.
§ 1.5. Скорость и ускорение точки при координатном способе задания движения
Скорость точки при координатном способе задания движения
Обозначим через
![]() -
проекции вектор скорости
на соответствующие оси произвольно
выбранной системы координат
-
проекции вектор скорости
на соответствующие оси произвольно
выбранной системы координат
![]() .
Тогда
.
Тогда
![]() .
(1.30)
.
(1.30)
Кроме того, как было показано выше, радиус-вектор точки может быть представлен через свои проекции по формулам:
=![]() ,
(1.31)
,
(1.31)
где
![]() -
это функции из уравнений движения точки
(1.17). По (1.13) с учетом (1.30) и (1.31) имеем:
-
это функции из уравнений движения точки
(1.17). По (1.13) с учетом (1.30) и (1.31) имеем:
![]() =
=
![]() (1.32)
(1.32)
Два вектора равны, если их одноименный проекции на оси одной и той же системы координат равны. Тогда из (1.32), получим:
![]() ,
,
![]() ,
,
![]() (1.33)
(1.33)
Здесь точки над функциями означают дифференцирование по времени. Итак,
1.20. Проекции вектора скорости равны первым производным по времени от соответствующих функций закона движения точки (1.7).
По
проекциям вектора скорости (1.33)
определяется и его модуль
![]() .
.
![]() (1.34)
(1.34)
С осями Оx, Оy, Оz вектор скорости образует, соответственно, углы α1, β1, γ1, косинусы которых определяются по формулам :
![]() (1.35)
(1.35)
Для направляющих косинусов вектора скорости имеет место равенство:
![]() (1.36)
(1.36)
Ускорение точки при координатном способе задания движения.
Обозначим через
![]() -
проекции вектор ускорения
-
проекции вектор ускорения
![]() на соответствующие оси произвольно
выбранной системы координат
.
на соответствующие оси произвольно
выбранной системы координат
.
Вектор ускорения
![]() можно
записать через его проекции
можно
записать через его проекции
![]() .
(1.37)
.
(1.37)
Тогда из (1.15) с учетом формул (1.30), (1.31), (1.33) получим:
![]() (1.38)
(1.38)
Или
![]() (1.39)
(1.39)
Здесь две точки над функциями означают вторую производную по времени от соответствующих функций, одна точка над функциями означает первую производную по времени от соответствующих функций. Итак,
1.21. Проекции
вектора ускорения
![]() равны первым производным по времени от
соответствующих проекций вектора
скорости
равны первым производным по времени от
соответствующих проекций вектора
скорости
![]() или вторым производным по времени от
соответствующих функций
закона движения (1.7).
или вторым производным по времени от
соответствующих функций
закона движения (1.7).
По известным проекциям вектора определяются его модуль и направляющие косинусы.
![]() (1.40)
(1.40)
Обозначая углы, которые образует вектор с положительными направлениями осей Оx, Оy, Оz через α2, β2, γ2, для направляющих косинусов получаем формулы:
![]() (1.41)
(1.41)
![]() (1.42)
(1.42)
