Вектор скорости точки в данный момент времени.

Будем вычислять среднюю скорость точки на убывающих интервалах времени . Другими словами, перейдем к пределу в отношении (1.12), устремив к нулю.

Итак, (1.13)

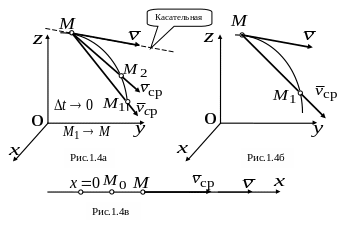
При , . Следовательно, вектор будет вращаться относительно точки и в пределе стремится занять положение касательной к траектории в точке (рис.1.4а). На рис.1.4б показаны оба вектора скоростей точки. На рис.1.4в показан случай прямолинейного движения точки. Поскольку касательная к прямой в любой её точке совпадает с самой прямой, то при прямолинейном движении оба вектора и направлены по траектории движения точки (рис.1.4.в).

1.15. Вектором скорости точки в некоторый момент времени называется вектор , приложенный своим началом к движущейся точке, направленный по касательной к траектории в этой точке в сторону перемещения точки. Он равен первой производной по времени от радиус - вектора точки (1.13).

Основной единицей измерения скорости в системе СИ является . Точка над вектором означает дифференцирование радиус-вектора по времени.

Вектор среднего ускорения точки, вектор ускорения точки

По аналогии с векторами скорости вводятся понятия вектора среднего ускорения точки и вектор ускорения точки в данный момент времени. Они характеризуют изменение соответствующих векторов скорости или за промежуток времени , или в данный момент времени.

1.16. Вектором среднего ускорения точки за промежуток времени называется отношение приращение вектора скорости, произошедшее за данный промежуток времени, к самому промежутку времени.

. (1.14)

0

Рис. 1.5а

Рис.1.5б

0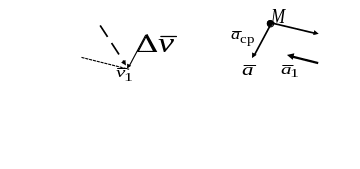

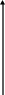
Из формулы (1.14) следует, что вектор среднего ускорения параллелен вектору приращения скорости = , где - вектор скорости точки в , – вектор скорость в точке траектории . Этот вектор, построенные по правилу параллелограмма, показан на рис.1.5а.

Переходя к пределу в формуле (1.14), получим формулу для вычисления вектора ускорения точки в данный момент времени:

.

. (1.15)

1.17. Вектором ускорения точки в некоторый момент времени t называется приложенный своим началом к точке и направленный в сторону вогнутости траектории вектор , равный первой производной по времени от вектора скорости точки.

В Международной системы СИ, как видно по формулам (1.14),(1.15), величина ускорения измеряются в .

На рисунке 1.5.б. векторы ускорения показаны в двух точках траектории. В точке векторы и «сонаправлены» - точка движется ускоренно (модуль вектора скорости увеличивается). В точке векторы и «не сонаправлены» - точка движется замедленно (модуль вектора скорости уменьшается).

Учитывая, что сам вектор скорости вычисляется по формуле (1.13), формулу (1.15) можно переписать еще в другом виде:

. (1.16)

Следовательно, можно дать второе определение вектора ускорения.

1.18. Вектором ускорения точки в некоторый момент времени t называется приложенный своим началом к точке и направленный в сторону вогнутости траектории вектор , равный первой производной по времени от вектора скорости или второй производной по времени от радиуса вектора точки.

В подробных курсах доказывается, что вектор ускорения лежит в соприкасающейся плоскости к траектории (надо вспомнить геометрию пространственных кривых). Если движение точки М происходит в плоскости, то её траекторией является плоская кривая. Для плоских кривых соприкасающаяся плоскость – это плоскось самого рисунка.