§ 1.3. Вектор перемещения, вектор скорости и вектор ускорения точки

Важнейшей характеристикой движения является понятие механической скорости и механического ускорения (или замедления). Только в механике даются точные определения этих понятий, которые затем используются не только для характеристики механической формы движения, но для характеристики любых других форм движения. Например, говорят о скорости роста или старения биологических объектов, скорости протекания химических реакций, скорости увеличения информации, скорости старения используемых технологий, скорости роста валового национального продукта, скорости роста благосостояния народа и так далее и тому подобное. Что же такое скорость и ускорение? На уровне бытового языка можно было бы сказать, что скорость – это «быстрота» происходящего движения. Ускорение – это «быстрота» изменения самой скорости, то есть – это уже скорость изменения самой скорости. Для инженерных расчетов этих определений, конечно, недостаточно. Ниже дается математически строгое определение этих понятий.

Вектор перемещение точки при прямолинейном движении

1.11. Движение точки называется прямолинейным, если она движется по прямолинейной траектории.

Положение движущейся точки М на траектории в разные моменты времени будем обозначать той же буквой М, но с разными индексами. Например, , и т.д. Положение точки на траектории в произвольный момент времени будем обозначать буквой . Пусть за промежуток времени точка М переместилась из положения в последующее положение . В начальный момент времени положение точки определяется радиус-вектором , положение точки определяется радиус-вектором . Положение точки в произвольный момент времени определяется радиус-вектором . Радиус-вектор точки получает приращение (рис.1.2). При этом

.

Если точка, двигаясь в положительном направлении оси (рис.1.2а), перемещается вправо из точки в точку , то радиус-вектора получает приращение . При этом вектор направлен в ту же сторону, что и (по направлению движения).

Если точка двигалась в отрицательном направлении оси (рис.1.2б) и переместилась влево из точки в точку , то и вектор приращения радиус-вектора направлен в отрицательном направлении оси (то есть пять по направлению движения).

,

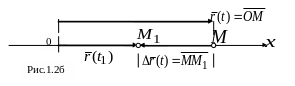
Все вектора должны лежать на оси , некоторые из них показаны в стороне от оси для большей наглядности.

1.12. Перемещением точки , которое произошло за время , из положения в положение называется вектор , равный приращению радиус-вектора точки и направленный по направлению движения точки из положения в положение .

С понятием перемещение точки тесно переплетается и понятие «путь пройденный точкой». Рассмотрим два возможных варианта движения:

1) Точка движется только в одном направлении, удаляясь или приближаясь к началу координат. На рис. 1.2а точка удаляется от начала координат, а на рис. 1.2б. приближается к началу координат. В этом случае путь , пройденный точкой, будет равен модулю вектора перемещения, то есть длине отрезка .

= .

2) Точка с момента времени некоторое время движется вправо от точки к точке оси . Радиус-вектор получает приращение . Точка останавливается в точке и продолжает движение в обратном направлении от точки к точке (см. рис. 1.2в). При точка вновь оказывается в точке оси . Радиус – вектор точки получает приращение ( ). Обратный путь точка проделывает за время . Полное время движения точки = = . Вектор полного перемещения точки за время движения точки обозначим (см. рис.1.2в). Полное перемещение точки складывается из перемещений точки в одну и в другую стороны.

= + +( ) = 0.

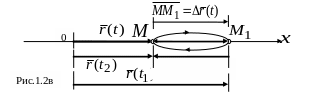
Путь , пройденный точкой за рассматриваемый промежуток времени, в нашем примере будет равен:

.

В рассматриваемом примере вектор полного перемещения точки оказывается равным нулю, в других случаях он отличен от нуля. Равенство нулю вектора полного перемещения точки может означать, что: 1) Точка в течении рассматриваемого промежутка времени пребывала в покое. 2) В течении рассматриваемого промежутка времени движение точки происходило так, что к концу промежутка времени точка вернулась в своем первоначальном положении .

Как видно из приведенного примера, путь пройденный точкой в общем случае не может быть вычислен только по приращению векторной координаты точки (по вектору полного перемещения ). Необходимо знать «историю» движения за промежуток времени .

1.13. Таким образом, путь , пройденный точкой за время , является сугубо положительной величиной и равен сумме длин участков траектории по которым двигалась точка в течении времени . В основных единицах системы СИ путь измеряется в метрах.

Вектор перемещение точки при криволинейном движении

Определение 1.12 справедливо и в этом случае. Отличие состоит в том, что теперь вектор перемещения направлен по хорде дуги в направлении движения точки (рис.1.3). Путь пройденный точкой в этом случае определяется не длиной отрезка, а длиной дугу , которая охватывает хорду (рис. 1.3).

Вектор средней скорости точки за промежуток времени .

1.14. Вектором средней скорости точки за промежуток времени назы­вается векторная величина , равная отношению вектора перемещения точки к промежутку времени, за которое это перемещение произошло.

( 1.12)

Так как деление вектора перемещения точки на положительное число не меняет направление вектора на обратное, то из формулы (1.12) видно, что вектор средней скорости направлен так же, как и вектор перемещения точки (рис. 1.3). При прямолинейном движении вектор лежит на траектории, при криволинейном движении (рис.1.3) вектор средней скорости направлен по хорде траектории в ту же сторону, что и вектор перемещения . В основных единицах системы СИ величина средней скорости измеряется в м/сек.

Пример 1.1. Мостовой кран за одну минуту перемещается на расстояние 80 м. Принимая кран за точку, определить его среднюю скорость в и .

Решение: В данной задаче речь идет о прямолинейном движении точки. Полагая в момент начала движения крана, Модуль вектора перемещения крана равен пройденному пути (рис.1.2а). Тогда

.

Замечание: Очевидно, что кран имел некоторые участки разгона и торможения, где его скорость в отдельные моменты времени не равнялась вычисленной нами средней скорости. Но для проектирования технологических процессов, например, для расчета среднего времени погрузки изделий на заводах железобетонных конструкций, знаний о средней скорости движения крана часто бывает достаточным.