§ 1.8. Законы равномерного и равнопеременного движений точки

В данном параграфе обсудим четыре типа движений точки, для которых относительно простым способом можно установить законы движения и определить кинематические характеристики (скорости и ускорения).

1. Прямолинейное равномерное движение точки.

Движение точки называется прямолинейным, если траектория точки есть прямая линия, для которой, как известно, радиус кривизны постоянен и равен бесконечности ( ).

Прямолинейное движение точки будет еще и равномерным, если точка движется с постоянной скоростью.

Другими словами, , , и, как следствие, вектор полного ускорения . При прямолинейном движении вектор скорости точки направлен параллельно траектории движения (прямо лежит на траектории) в сторону движения точки. При прямолинейном движении точки координатный и естественный способы задания движения полностью совпадают. Направим ось Оx по траектории в направлении движения точки (рис.1.16). Положение точки определяется одной координатой и, следовательно, закон движения по прямой задается одной функцией . Зададим начальные условия движения. Пусть в начальный момент времени , кинематическая точка находилась в точке прямой с координатой (рис.1.16).

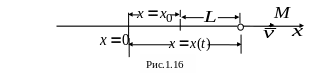
Необходимость в индексе х, например, в формулах (1.61) отпадает, так как движение точки происходит только вдоль известной оси . В направлении других осей движения просто нет (при прямолинейном движении всегда именно так надо выбирать оси координат). Тогда , , (это следует из условия прямолинейности и равномерности движения), и (это следует из условия прямолинейности движения). Проинтегрируем первое равенство из (1.61), при . Это потребует проведение следующих действий:

, , , ,

где С- постоянная интегрирования. Для определения константы интегрирования воспользуемся начальным условием: при , . Это приводит к уравнению . Тогда . Отсюда видно, что механический смысл константы интегрирования - это начальное положение (координата) точки .

Окончательно, уравнение равномерного прямолинейного движения точки и выражение для скорости этой точки принимают вид:

, (1.71)

Напомним, что в (1.71) величина скорости может быть положительна ( , точка движется в положительном направлении оси ) или отрицательна ( , точка движется в отрицательном направлении оси ). Если обозначить = - путь, пройденный точкой за рассматриваемый промежуток времени, тогда то, что в обыденной речи называют скоростью точки, можно вычислить по формуле . Надо помнить, что путь –это просто длина расстояния, пройденного точкой за некоторый промежуток времени, поэтому всегда . Например, если и точка все время двигалась в положительном направлении, то . Этот случай показан на рис.1.16.

Пример 1.10. Скорость движения эскалатора метрополитена равна . Определить скорость движения в и время, за которое эскалатор с пассажиром переместиться на расстояние .

Решение: Точки эскалатора совершают одинаковые прямолинейные равномерные движения. Поэтому достаточно рассмотреть движение любой ступеньки с пассажиром. Систему координат выберем так, как показано на рисунке к примеру. Тогда:

.

.