1.28. Движение точки м по траектории будет ускоренным, если векторы и направлены по касательной к траектории в одну сторону, и движение точки будет замедленным в противном случае.

1.29. Движение точки м по траектории будет ускоренным, если произведение , и движение точки по траектории будет замедленны, если .

Действительно, если, например, , то это означает, что одновременно и или и . В первом случае точка М движется ускоренно (рис.1.9) в положительном направлении оси (направление движения точки всегда определяется или по направлению вектора скорости , или по знаку величины алгебраической скорости ). Во втором случае точка движется ускоренно в отрицательном направлении оси . Если , то это означает, что в один и тот же момент времени и имеют разные знаки, а точка М движется замедленно в положительном направлении оси , если , и в отрицательном направлении оси , если .

Модуль вектора ускорения при естественном способе задания движения определяется по формуле:

, (1.54)

где а_, а_n вычисляются по формулам (1.53).

Тангенс угла отклонения μ вектора полного ускорения точки от направления Мn (рис.1.9) вычисляется по формуле

(1.55)

, если и , если , так как - всегда больше нуля. Другими словами, при ( ) вектор полного ускорения точки отклоняется в сторону оси (рис. 1.3) или в сторону положительного направления оси . Рассмотрим пример.

Пример 1.5. Точка движется по криволинейной траектории согласно закону (м) (здесь – в секундах). Определить модуль и направление вектора скорости в момент времени .

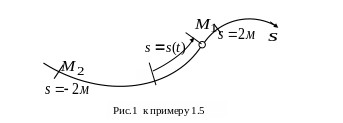
Решение. Итак, по условию задачи траектория считается известной. Пусть она имеет вид, показанный на рис. 1 к примеру. На траектории зададимся началом криволинейной системы координат, где будет , и положительным направлением оси . Точка движется по траектории по закону . Чтобы представить себе закон движения этой точки, надо знать элементарные функции и их графики. Для функции график представлен на рис. 2. Во - первых, график функции показан только для значений аргумента (времени) , так как параметр времени не может принимать отрицательные значения.

При точка находится в начале координат . Во – вторых, по графику функции видим (рис.2), что координата точки сначала растет в положительном направлении до значения . Это соответствует промежутку времени (при , как известно, функция ). Это означает (рис.1), что в промежутке точка удаляется от начала координат на расстояние . Что происходит дальше? Вернемся опять к графику закона движения (рис.2). По графику видим, что координаты точки убывают в промежутке времени сначала до нуля, а при координаты точки становятся даже отрицательными. Другими словами, в промежутке времени материальная точка из положения движется в отрицательном направлении оси, сначала к началу координат (рис.1) и далее точка от точки продолжает движение к точке траектории. Максимальное удаление точки в отрицательную сторону . А координата точки траектории , в которую приходит материальная точка в момент времени будет .

Далее, как видно по графику уравнения движения (рис. 2), все будет повторяться. Такие повторяющиеся движения, которые описываются периодическими функциями синусов или косинусов, принято называть колебательными движениями. Таким образом, движение материальной точки является колебательным движением около начала координат с амплитудой . Заметим, что амплитуда колебательного движения «2» является коэффициентом в уравнении движения точки .

Закон изменения скорости точки определим по (1.51):

.

Отсюда видим, что алгебраическое значение скорости тоже описывается периодической функцией. График этой функции представлен на рис.3. По графику (рис.3) видим, что модуль скорости меняется с течением времени от нуля до 6,28 (м/c). Кроме того, величина скорости равна нулю в моменты времени и т.д. В указанные моменты времени (см. рис.2) материальная точка имела координаты (точка или траектории). Другими словами, в точках , траектории материальная точка имеет на некоторое мгновение скорости равные нулю (мгновенный покой). В этих точках ( и ) движущаяся материальная точка меняет направление движения на обратное (следовательно, и вектор скорости меняет направление на обратное). Не остановившись нельзя изменить направление движения на обратное. Направление вектора скорости при естественном способе задания движения определяется по знаку алгебраического значения скорости. При получаем: . Другими словами, точка находится в начале координат (точка на рис.1 и рис.4). При получим .

Знак минус у алгебраического значения скорости (у производной ) говорит о том, что точка в данный момент времени движется в отрицательном направлении оси ,

то есть от точки к точке . Следовательно, вектор скорости направлен в точке по касательной к траектории в сторону точки . Модуль вектора скорости равен модулю алгебраического значения скорости . Ответ: Модуль скорости точки равен , а вектор скорости направлен по касательной к траектории в отрицательном направлении оси (рис.4 к примеру 1.5).