1.2.6. Эпр плоской круглой пластины

Для схождения ЭПР плоской круглой пластины радиусом , можно так же воспользоваться формулой (1.21.)

Где следует положить

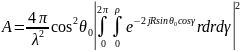
Воспользовавшись представлением функции Бесселя, получим :

,

Где J(Z) – функция Бесселя первого порядка.

Формула (30) дает удовлетворительные результаты лишь при услови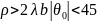и . при 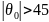она дает не только количественно, но и качественно неверные результаты . В этом случае вместо формулы (30) можно использовать следующее представление:

,

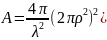Которое дает хорошее согласие с экспериментом при условии .

При скользящих углах (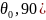 хорошие результаты дает формула:

Из которой следует ,что в области скользящих углов падения ЭПР в зависимости от R

В области малых радиусов ЭПР диска , когда существенно меньше длины волны ЭПР может быть рассчитан для горизонтальной поляризации по формуле :

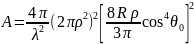, а для вертикальной –

При нормальном падении имеем:

На рис.1.13. приведена зависимость отношения

Наибольшее относительное значение ЭПР, равное наблюдается при что очень близко к условию

1.2.7. Эпр треугольной пластины

Рассмотрим бесконечно тонкую идеально проводящую пластину, имеющую вид равнобедренного треугольника с основанием 2а и выстой В при естественном допущении и определим ее ЭПР в направлении, определяемой углами

Для случая можно непосредственно воспользоваться формулой (1.17). которая дает :

независимо от вида поляризации падающей волны.

Чтобы найти ЭПР треугольной пластины при произвольных углах и , целесообразно использовать соотношение (1.21). Однако в виду крайней громоздкости получающихся соотношений ограничимся рассмотрением ЭПР при определении ее в двух взаимо-ортогональных плоскостях, перпендикулярных плоскости пластины

Для первого случая (горизонтальная плоскость , из формулы (1.21) имеем :

Для второго случая (вертикальная плоскость также из формулы (1.21). имеем :

Полученные формулы достаточно хорошо согласуются с экспериментальными данными.

В горизонтальной плоскости ДОР представляет собой достаточно быстро ( при изменении угла наблюдения ) осциллируюшую функцию, при этом ширина главного лепестка ДОР по уровню 0.5 составляет в уровень первого бокового лепестка -26.6 дБ . в вертикальной плоскости –напротив, ДОР является монотонной функцией , не имеющей лепестков. Ширина главного лепестка по уровню 0.5 при условии

Кроме пластин в форме равнобедренного треугольника на практике часто встречаются пластины в форме прямоугольного треугольника, для которых остаются справедливыми формулы (1.32) и (1.33) .Это свидетельствует о том ,что их ДОР представляют собой монотонные финкции, не имеющие лепестковой структуры. Более того , можно утверждать , что любые треугольники с основание А и вытой В в вертикальной плоскости также будут иметь безлепестковую ДОР.

1.2.8. Эпр малых и соизмеримых с длиной волны целей методы расчета эпр, изложенные в 1.2 , оказываются непригодными . Получим ряд соотношений , относящихся к этим случаям.

Для целей , у которых размеры Л много меньше ,ток, наведенный на их поверхности, можно считать не только равным по амплитуде в каждой точке, но и синфазным. Воспользуемся результатами, полученными в теории антенн, для рассматриваемого случая. Наведенная ЭДС будет ЭДС равна Е и Л , где -напряженность электрического поля падающей волны. Сопротивление Z , носящее емкостной характер, может быть рассчитано по формуле , где имеет порядок 1 кОм. С учетом сказанного легко получить выражение для тока в проводе:

Напряженность электрического поля в точке приема можно найти на основании теории элементарного вибратора:

Откуда с учетом формулы(1.8) получаем следующее выражение для ЭПР цели, размеры которых много меньше

Как видно, ЭПР пропорциональна шестой степени их размера и обратно пропорциональна четвертой степени длины волны. С такой зависимостью мы уже встречались в п.1.2.1 при рассмотрении ЭПР малых шариков (1.22), Различные только в коэффициентах, которые состаляют для шара ,для вибратора . если вместо радиуса шара взять его диаметр , то коэффициент будет , а его отношение составит 17. Это позволяет удержать , что практически для всех малых тел величина их ЭПР будет ограничена неравенством:

Где пол следует понимать максимальный линейным размер. Для диска в соответствии с формулой (1.37) получим коэффициент, равный 0.18 .

Хотя неравенство (1.37) относится к случаю оно позволяет понять практически важное положение о том , что в радиолокации можно применять лишь сравнительно короткие волны ,т.к. нельзя получить интенсивного обратного рассеяния, если длина волны велика по сравнению с линейными размерами цели. Поэтому совершенно не случайно верхняя граница используемых в радиолокации длин волн лежит в метровом диапазоне.

В случаи, когда размеры целей становятся соизмеримыми с длиной электромагнитных волн, начинают проявляться эффекты, подобные явлению резонанса , и происходит резкое возрастание наводимых в цели поверхностных токов.( Об этом уже частично говорилось в предыдущих разделах). Естественно , что зависимость ЭПР от отношения в этом случае будет носить осциллирующий характер .

Для полуволнового вибратора первые равенства формул( 1.34) и (1.35) останутся в силе, только вместе следует подставить действующую высоту такого вибратора, равную , а вместо сопротивления Z- соответствующую ему величину 73 Ом. С учетом сказанного вместо соотношения (1.36) будем иметь :

Полученный результат показывает , что ЭПР полуволнового вибратора при резонансе значительно превышает его собственную геометрическую площадь.

В соответствии с рис. 1.13 для круглого диска при имеем:

Эта же формула справедлива и для тонкой квадратной пластины с размером стороны

Кривые, приведенные на рис. 1.6 , дают для сферы диаметром следующее значение максимальной ЭПР:

Из графиков рис.1.10 можно получить аналогичное выражение для цилиндра , у которого площадь поперечного сечения равно площади резонансного диска , а радиус основания соответствует максимуму ЭПР , т.е.

Полученные соотношения также дают возможность записать неравенство аналогичное (1.37 для целей , у которых один из характерных размеров примерно равен :

Или в терминах этого размера :

Обращает на себя внимание факт, что резонансное значение ЭПР сферы диаметром оказывает меньше, чем ЭПР вибратора такой же длины. Это является следствием того , что излучение от дальних участков сферы оказывается не только не в фазе с излучением от ближних ее участков , но и даже близко к противофазному.

1.3. Характеристики искусственных отражателей

1.3.1. уголковые отражатели

В ряде случаев требуется создание специальных искусственных целей. Подобная задача возникает при калибровка и настройке радиолокационных станций, при анализе структуры облачности , при определении направления и скорости ветра . Большую роль искусственные отражатели играют для обозначения целей , которые желательно видеть с борта летательного аппарата, для создания ложных целей и маскировки тех или иных воздушных или наземных целей.

К искусственным можно отнести все типы отражателей, рассмотренных в разделе 1.2. Кроме того , широкое распространение получили так называемые уголковые отражатели, представляющие собой дву или трехгранные углы с боковыми стенками, выполненными в виде квадратных, треугольных или секторных граней ( рис .1.15. а-в). Используются также уголковые отражатели с гранями произвольной формы (рис. 1.15. г)

Металлические двугранные уголковые отражатели представляют собой простейший тип радиолокационных отражателей. На практике из-за того ,что они являются широкоугольными отражателями только в одной плоскости, используются редко. Тем не менее изучение рассеивающих свойств двугранных уголковых отражателей представляет большой интерес для объяснения и понимания свойств трехгранных отражателей . Кроме того, двугранные отражателей часто входят как составные элементы в различные конструкции.

Двугранный уголковый отражатель состоит из двух плоских металлический граней, в общем случае произвольной формы , развернутых чаще всего под углом 90 ( рис .1.16)

В предположении, что размеры граней ОС и ОД много больше допустима лучевая трактовка процесса отражения . Луч 1 после отражения от граней ОС и ОД изменит свое направление на 180 и переотразится в сторону источника волны( луч 2).

Считая фазу волны в точке N равной нулю, найдем ее фазу в точке M , которая , естественно , будет пропорциональна длине ломаной прямой NABM . из рис 1.16 следует :

Равенство (1.38) показывает , что фаза волны в точке М не зависит от положения точки А , а поэтому фазы всех лучей (3- 8) на плоскости FC будут одинаковыми. С позиции наблюдателя перед ним будет синфазная излучающая площадка размером СН на -длину третьей стороны уголкового отражателя ( перпендикулярной плоскости рис. 1.16)длина СН определяет элементарно . она равна : . Таким образом , в соответствии с формулой (1.17) ЭПР рассматриваемого отражателя будет :

Если боковые грани считать одинаковыми , т.е. ОС=ОД , то при точка Р на рис .1.16 совместится с точкой Д , и при дальнейшем росте угла размер излучающей площади СН меняться не будет так как луч № после отражения не будет попадать на вторую грань. Это означает , что формула ( 1.39) справедлива при а поэтому при ЭПР будет равна своему максимальному значению

Основная особенность двугранного уголкового отражателя состоит в том , что он создает кроссполяризованное рассеянное поле.

Двугранный уголковый отражатель делается малоэффективным , когда падающий луч отклоняется от плоскости, нормальной к ребру. Этот недостаток устраняется применением третьей грани, перпендикулярной двум основным . Наиболее часто встречаются треугольные, секторные и квадратные грани ( рис.1.15). Внутренние поверхности граней, если они достаточно велики по сравнению с , образуют систему из трех зеркал. При падении на них пучка лучей после трехкратного отражения формируется пучок лучей, распространяющийся в направлении, обратном направлению падения.

Это свойство характерно только для тех взаимоперпендикулярных граней. Четыре, пять и более граней не дают подобного эффекта. Для трехгранного уголкового отражателя свойство обратного отражения сохраняется в широком секторе углов падения, что дает возможность представить его в виде эквивалентного плоского зеркала, расположенного перпендикулярно направлению падения.

Трехгранные уголковые отражатели в радиолокации используется в качестве эталонов ЭПР, навигационных знаков, пассивных маяков, реперов, мишеней и т.д.

Все существующие методы расчета и ЭПР сводятся к апертурному методу, при этом вся сложность расчета состоит в определении величины эквивалентной площади S , входящей в формулу (1.17) Ход лучей в трехгранном уголковом отражателе схематически показан на рис. 1.15а.

Расчет максимального значения ЭПР отражателя, имеющего длину ребра а с треугольными гранями, приводит к формуле:

Максимальный ЭПР при секторных гранях оказывается примерно в 4 раза большим:

А при квадратных – в 9 раз

Если размеры отражателей уменьшаются и становятся соизмеримыми с длиной волны или меньшими , то формулы ( 1.40) – (1.42) оказываются несправедливыми. Для определения ЭПР в таком случае можно воспользоваться графиком рис.1.17. где показано отношение ЭПР для трехгранного уголкового отражателя с треугольными гранями к его значению, найденному по формуле (1.40) , то отношения длины ребра а к . Как видно , при а=5 ошибка расчета ЭПР по формуле ( 1.40) составляет 20 %

На практике иногда все –таки используют в качестве грубых эталонов ЭПР уголки малых размеров вплоть до . Это объясняется тем , что даже уголок малых размеров обладает гораздо большим ЭПР, чем примерно равные ему по размеру сфера или цилиндр.

Важное значение имеет точность изготовления уголкового отражателя. Чем больше линейные размеры граней, тем точнее должен быть выдержан угол 90 между ними. Так, например, при неточность в I уменьшает величину ЭПР в 10 раз , при - в 3.5 раза. Проиллюстрируем сказанное численным примером. Уголковый отражатель с треугольными гранями 125 см на волне 3.2 см должен был иметь . При отклонении углов от прямых на I значение станет равным 300 м2.