МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ДЕПАРТАМЕНТ ВОЗДУШНОГО ТРАНСПОРТА

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ГРАЖДАНСКОЙ АВИАЦИИ

Кафедра системотехники

А.И. Козлов, А.И. Логвин

Отражательные характеристики радиолокационных целей

Разрешено к изданию в качестве

Учебного пособия для студентов

Специальности 23.04

Москва 1995

ББК 0571.55

К59

Печатается по решению редакционное издательского совета московского государственного технического университета ГА

Рецензенты: канд.техн.наук, доц. В.В.Соломенцев;

д-р физ.-мат.наук, проф. А.Г.Горелик.

Козлов А.И., Логвин А,И.

K59 Отражательные характеристики радиолокационных целей: Учебное пособие. - М.: МГТУ ГА, 1995. - 68 с.: Ил. 38, табл. 5, список лит.: 4 наим.

ISBN 5-86311-078-3

Данное учебное пособие "Отражательные характеристики радиолокационных целей" по дисциплине "Теоретические основы радиолокации" издается в соответствии с учебной программой для студентов 4 курса дневного обучения и 5 курса заочного обучения специальности 23.04.

Рассмотрено и одобрено на заседаниях кафедры 14.09.95 г. и методического совета 21.09.95 г.

3206040000-013 ББК 0571.55

Ц33(03)-95 Св.тем.план 1995 г.

поз, 13

КОЗЛОВ Анатолий Иванович,

ЛОГВИН Александр Иванович

ОТРАЖАТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ

РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ

Учебное пособие

Редактор Л.Е.Паталова Корректор И.В.Вилнова

ЛР № 020580 от 23.06.92 г. Подписано в печать 29.01.95 г.

ОТРАЖАТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ

РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ

Введение

Радиолокация - это область науки и техники, обеспечивающая получение радиотехническими методами сведений об объектах (целях), включающих в себя их обнаружение и измерение параметров принимаемых злектромагнитных волн, характеризующих относительное положение и скорость взаимного перемещения радиолокационной станции (РЛС) в целей, а также размеры целей, их конфигурацию, ориентацию, отражающие свойства и т.д.

Из сказанного видно, что радиолокацию нужно рассматривать как средство дистанционного зондирования радиолокационных целей, которы-ми могут быть любые объекты исследования, включая самолеты, вертолеты, космические аппараты, а также земную поверхность, гидрометеооб-разования и пр. Носителем информации о радиолокационных целях является рассеянная или электромагнитная волна, которая может быть зафиксирована приемным радиотехническим устройством, входящим в состав РЛС. При любом способе обработки радиолокационных сигналов названная информация может быть извлечена, а затем интерпретирована только путем сравнения посланной и принятой электромагнитных волн.

При решении радиолокационных задач ГА в подавляющем большинстве случаев РЛС и цели находятся достаточно далеко, что дает возможность считать падающую волну в окрестности цели и рассеянную у антенны - плоскими, которые могут быть описаны при помощи только одного электрического вектора Е . Ограничиваясь случаем однопозиционной радиолокации, когда приемная и передающая антенны совмещены в пространстве, что характерно для РЛС ГА, проблема получения информации о радиолокационных целях, в конечном счете, сведется к сравнению электрических векторов излученной Еи ж принимаемой Еп электромагнитных волн у антенны. Так как в общем случае антенна излучает эллиптически поляризационную волну (в частности, линейную, круговую), а отраженная также является таковой, то целесообразно вместо вектора Е использовать два его ортогональных компонента - горизонтальный (Г)-Ег и вертикальный (В)-Ев.

В связи с тем, что процесс рассеяния электромагнитных волн является линейным, между независимыми составляющими рассеянной и излу-

ченной волн существует линейная зависимость. Практически для всех радиолокационных целей в пределах ширины спектре реальных излучаемых сигналов отражательные свойства этих целей на всех частотах спектра остаются неизменными. Это позволяет, с учетом сказанного, связать компоненты электрического вектора излученной волны в окрестности цели с соответствующими компонентами рассеянной волны у антенны при помощи следующих равенств:

Где S_m,n - некоторые коэффициенты пропорциональности ( m,n =r,B );

Ψ_m,n -соответствующие S_m,n фазы;

-горизонтальный и вертикальный компоненты излученной волны,

а - принимаемой.

В формуле (I.I) принята комплексная форма записи гармонического колебания, т.е. вместо выражения Acos(ωt +β) используется запись Ае^jωt e^jβ.

В рамках общей теории отражения электромагнитных волн показано, что для однопозиционной радиолокации S_Br = S_rB и Ψ_Br = Ψ_rB .

Систему (I.I) удобно представить в матричном виде:

В равенстве (1.2) вместо индексов r и B введены индексы I и 2 соответственно. Если для матриц-столбцов ввести обозначение Е_n и Е_u , а для квадратной матрицы:

то соотношение (1.2) можно представить в компактной форме:

Из представлений (1.2) я (1.4) наглядно видно, что в рамках проведенного рассмотрения отражательные свойства цели характеризуются матрицей S , носящей название матрицы рассеяния (1.3). Более того, так как равенство (1.1) устанавливает общий вид линейной связи между электрическими векторами излученной и принимаемой электромагнитными волнами, матрица рассеяния является наиболее общей характеристикой отражательных свойств цели. В реальных условиях работы РЛС из-за непрерывного изменения взаимного положения антенны и цели все элементы матрицы рассеяния в общем случае случайным образом меняются, а поэтому наиболее полной характеристикой радиолокационной цели являются соответствующие многомерные законы распределения.

Перейдем к рассмотрению наиболее простого, но имеющего важное значение случая, когда ни один из элементов матрицы S не меняется во времени. Это соответствует ситуации, когда неподвижный луч антенны "смотрит" на неподвижную цель. Как видно из формулы (1.3), цель в этом случае описывается шестью числами: S₁₁, S₁₂, S₂₂, Ψ₁₁, Ψ₁₂, Ψ₂₂ . Это означает что максимальное число независимых параметров, которые можно получить из измерения, также равно шести. Разберем их физический смысл. Для этого вернемся к системе (1.1). Пусть излучается горизонтально поляризованная волна ( =0 ), тогда будем иметь:

откуда получаем для S_rr и S_rB :

а для фаз Ψ_rr и Ψ_rB :

Таким образом, аргумент отношения горизонтального компонента принимаемой волны у антенны к аналогичной величине излученной волны у цели равен фазе Ψ_rr , а модуль этого отношения - величине S_rr. Аргумент отношения вертикального компонента принимаемой волны у антенны к горизонтальному компоненту излученной волны у цели (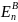 = 0) равен Ψ_rB, а модуль этого отношения - величине S_rB . Аналогичный смысл имеют S_BB и S_rB при этом должен рассматриваться случай излучения вертикально поляризованной волны ( = 0).

Элементы матрицы рассеяния S₁₁ и S₂₂ называются основными, а S₁₂ - кроссовым или перекрестным.

Измерения абсолютных значений Ψ₁₁, Ψ₁₂, Ψ₂₂ сопряжены с большими трудностями, поэтому, как правило, ограничиваются их относительными значениями Ψ₁₂ - Ψ₁₁ , Ψ₂₂ - Ψ₁₁, что эквивалентно тому, что фазу Ψ₁₁ принимают равной нулю. Большие трудности порождаются и при измерении абсолютных значений S₁₁ , S₁₂, S₂₂ , а поэтому также проводят относительные измерения и определяют отношения S₁₂/S₁₁ и S₂₂/S₁₁, что эквивалентно тому, что S₁₁ кладут равным единице. При таком подходе цель описывается не шестью, а четырьмя параметрами.

К дальнейшему анализу свойств матрицы рассеяния мы вернемся несколько позже, а сейчас перейдем к рассмотрению наиболее распространенного в настоящее время случаю, когда РЛС работает только на одной фиксированной поляризации как в режиме передачи, так и в режиме приема. При этом, как правило, есть возможность проводить только измерение сигнала, пропорционального S₁₁ . Ясно, что при такой ситуации цель описывается только одним числом S₁₁. Так как по определению S₁₁ связывает поля, измеряемые в разных точках (одно у цели, другое у антенны), то, очевидно, S₁₁ зависит от расстояния, что порождает определенные неудобства. На практике широкое распространение получил несколько иной параметр. Введем его. Поскольку в дальнейшем речь идет только о случае, соответствующем приему и излучению на одной и той же поляризации, индексы у Е и S , где в этом не будет особой необходимости, писать не будем.

Пусть РЛС через антенну с коэффициентом усиления D излучает электромагнитную волну мощностью . Тогда значение плотности потока мощнооти П у цели, находящейся на расстоянии R от антенны, будет:

Очевидно, что в направлении на антенну рассеется волна, мощность которой Р_р пропорциональна величине П_u , определяемой равенством (1.6). Коэффициент пропорциональности при этом должен иметь размерность площади. Обозначим его А , тогда

а поэтому плотность потока мощности рассеянной волны П_n у антенны будет определяться при помощи равенства:

Так как величина П пропорциональна квадрату модуля электрического вектора, то из первого равенства в выражении (1.5) с учетом (1.6) и (I.7) получаем:

Достоинство введенного параметра А состоит в том, что он не зависит от расстояния, хотя в формулу (1.8) он входит в явном виде. Это объясняется тем, что Е_п пропорциональна величине Е_u/R, а поэтому А определяется только целью. Коэффициент А называется эффективным поперечником (площадью) рассеяния (ЭПР) или эффективной отражающей площадью (ЭОП) и является основной характеристикой радиолокационных целей. Аналогично можно получить выражения ддя А₁₂ и А₂₂ .

При изменении взаимного расположения антенны и целя ЭПР, очевидно, будет изменяться. Зависимость ЭПР от азимута и угла места называется диаграммой обратного рассеяния (ДОР).

Для того, чтобы рассчитать ЭПР и ДОР, необходимо провести решение соответствующей дифракционной задачи, что сопряжено с серьезными математическими и вычислительными трудностями, а поэтому здесь нашли широкое применение различные приближенные методы. Перейдем к их рассмотрению.

I.I. Основные методы расчета эпр

Расчет ЭПР в подавляющем большинстве случаев сводится к решению соответствующих дифракционных задач, определение необходимых поляризационных компонентов рассеянного поля и последующем начислении ЭПР пo формуле (I.I). Проведем краткий обзор некоторых методов, использующихся в настоящее время для расчета ЭПР.

Как известно, для того, чтобы найти рассеянное в заданной точке пространство, необходимо решить уравнения Максвелла с учетом соответствующих граничных условий. Этот путь ведет к так называемым строгим методам теории дифракции. Не следует, конечно, думать, что решение, полученное строгим методом, даст более точный ответ для реальных целей, чем полученное приближенным методом. Дело в том, что во всех случаях при расчете ЭПР радиолокационная цель с необходимостью заменяется приближенной идеализированной моделью, строящейся на базе таких моделей, для которых можно получить строгое решение. К сожалению, их круг ограничен весьма небольшим набором: сфера, сфероид, диск, тонкий провод и некоторый ряд других. Ошибка, возникающая вследствие такой замены, зачастую оказывается столь большой, что практически сводит на нет все достоинства строгих решений. В этой связи приближенные методы могут дать гораздо более точное решение, так как на этапе моделирования они позволяют учесть значительно большее число факторов, определяющих рассеяние поля. Тем не менее при строгих методах всегда есть возможность строго оценить ошибку полученных решений на всех этапах решения задачи, в то время как при использовании приближенных методов такой возможности практически нет, так как там математические трудности обходятся при помощи той или иной физической гипотезы.

Наибольшее распространение в радиолокации для расчета ЭПР целей получили приближенные методы: геометрической оптики и апертурный. Рассмотрим их подробнее.

В основе метода геометрической оптики лежат следующие физические допущения:

длина волны электромагнитного поля существенно меньше характерных размеров тел, с которыми поле взаимодействует;

границы раздела взаимодействующих о электромагнитным полем тел и сред идеально гладкие, а кривизна границ незначительна, так что в пределах небольших площадок границы раздела преломляют и отражают электромагнитные волны в соответствия о формулами Френели для плоской границы раздела;

распространение энергии электромагнитного поля происходит вдоль лучей;

в случае электрически неоднородных сред длина волны электрромагнитного поля в среде существенно меньше расстояния, на котором параметры среды заметно изменяются.

Применительно ко многим радиолокационным целям, перечисленным вше, условия являются вполне приемлемым, а поэтому получающиеся в рамках геометрической оптики решения являются вполне удовлетворительными. Пo существу этот метод применительно к большим хорошо проводимым телам дает возможность вычислять ЭПР, не используя никаких других законов электромагнетизма, кроме закона отражения в преломления Спеллиуса.

Проиллюстрируем сказанное на примере расчета ЭПР плоских и выпуклых тел, размера которых значительно превышают длину волны. Пусть плоская электромагнитная волна падает на такое тело (рис. I.I).

Рис. I.I. К иллюстрации геометрического приближения

Пря геометреоптическом приближении поверхность тела разбивается на две зоны: область тени и освещенную область. При этом надо считать, что под воздействием падающей волны никаких поверхностных токов в области тени наводиться не будет. Несмотря на то, что такое допущение является физически необоснованным, так как в области тени обязательно наводятся токи, вклад создаваемого ими поля в суммарное рассеяние очень мал, а поэтому названное допущение вполне корректно.

Рассмотрим окрестность точки B на рис. I.I, которая в силу предположения о том, что радиусы кривизны тела существенно больше длины волны λ , может быть заменена плоской большой (по сравнению с λ ) хорошо проводящей площадкой (рис. 1.2). Как известно из электродинамики, на рассматриваемой границе раздела нормальная составляющая магнитного вектора Ḣ_n должна равняться нулю. Это c необходимостью влечет за собой равенство длин магнитных векторов падающей Ḣ_пад к отраженной Ḣ_отр волн, под действием которых возникает, как это видно из рис. 1.2, тангенциальная составляющая суммарного магнитного вектора Ḣ=Ḣ_τ , равная удвоенной тангенциальной составляющей магнитного вектора падающей волны Ḣ_τпад. Тангенциальная составляющая вектора Ḣ приводит к возникновению электрического тока, плотность которого I будет определяться известным соотношением:

где - вектор нормали к поверхности.

Введем некоторую отсчетную плотность ММ (рис. 1.1) и обозначим через R_o расстояние от РЛС до этой плоскости, а через R расстояние от точки B ; значение магнитного вектора падающей волны в плоскости ММ будем записывать как Ḣ_опад.

Так как цель находится достаточно далеко от РЛС, то падающая волна может считаться плоской, и поэтому значение вектора Ḣ в точке В будет:

Где - волновое число, .

Таким образом, плотность тока на освещенной части поверхности может быть представлена в виде:

Выделив около точки В элементарный вибратор длиной dl и шириной db , по которому протекает ток dI=Idb и воспользовавшись известными из курсов электродинамики и антенных устройств формулами для магнитного вектора в дальней зоне, получим следующее выражение для этого вектора около приемной антенны:

Смысл угла α ясен из рис. 1.2, откуда видно, что произведение соsα x ds есть проекция освещенной области на плоскоcть, перпендикулярную направлению распространения падающей волны. Введем обозначение:

и проинтегрируем равенство (1.9) по освещенной области:

Так как в плоской волне электрический и магнитный векторы пропорциональны, то, воспользовавшись равенством (1.5) и (1.8), получим следующее выражение для ЭПР плоских и выпуклых тел, размеры которых существенно превосходят λ :

Под знаком интервала стоит быстро осциллирующая функция, а поэтому при небольшом изменении угла падения α ЭПР будет испытывать осцилляции тем больше, чем больше отношение линейных размеров тела к длине волны.

Формула (1.10), несмотря на внешнюю простоту, оказывается в ряде случаев неудобна, так как ведет к необходимости вычисления сложных интегралов. Однако при используемом допущении, что размеры тела и его радиусы признаны много больше длины волны, можно получить более компактное и удобное соотношение.

Введем два характерных размера тела ρ₁* ρ_е (это могут быть радиусы кривизна поверхности) и представим показатель экспоненты следующим образом:

Где обозначено:

С учетом этого запишем интеграл, входящий в формулу (1.10):

Под интегралом стоят быстро осциллирующие функции cos[py(x,y)]. Все подынтегральное выражение имеет характер колебания, изменяющегося по фазе по закону У(x,у) (рис. 1.3).

Зафиксируем сначала некоторое значение y=y₁. Тогда видно, что две соседние полуволны колебания (положительная и отрицательная) имеют почти равные площади и почти полностью погашают друг друга, в связи с чем величина интеграла резко падает с увеличением р. Однако эта компенсация соседних полуволн становится не эффективной в окрестности точки x=x₀ , где У’(x₀, у₁)=0. В таких точках, называемых точками стационарной фазы, "частота колебаний"рy”(x) стремится к нулю и колебательный процесс прекращается (рис. 1.3). Аналогичная ситуация имеет место и при изменении у . Поэтому величина интервала зависит главным образом от поведения подынтегральной функции вблизи точек (Хо, у0) , где У’_x=У_у’= О , причем по мере увеличения р существенные части области интегрирования уменьшаются.

Разложим функцию У(x,y) в ряд Тейлора в окрестности точки стационарной фазы (У’_x=У_у’= О):

и подставим ее представление в формулу (I.II):

где введены обозначения:

Проведя перегруппировку в показателе экспоненты и учитывая известное значение интеграла Пуассона:

получим:

(1.13)

Подставим полученное выражение в равенство (1.10) с учетом выражений

для р и У(x,у):

Применим эту формулу для расчета ЭПР выпуклой поверхности двойной кривизны. Рассмотрим параболоид, уравнение поверхности которого в прямоугольной системе координат может быть записано в виде:

где p₁ и p₂ - главные (наибольший и наименьший) радиусы кривизны в вершине параболоида х = у = 0.

Найдем точку стационарной фазы:

Таким образом, x₀=y₀ =o. Вычислим вторые производные в этих

точках:

Подставляя найденные значения в формулу (1.14), для ЭПР получим:

Так как поверхность второго порядка в окрестности точки наблюдения на выпуклой поверхности достаточно хорошо ее описывает, то формула (I.15) имеет достаточно общий характер. К такому же выводу можно прийти на основе следующих простых рассуждений. Выделим на поверхности тела малый элемент, перпендикулярный направлению падения и ограниченный дугами главных радиусов кривизны dS₁ и dS₂. В центре элемента располагается точка зеркального отражения (точка стационарной фазы или, как это принято говорить в радиолокации, блестящая точка). Мощность падающей волны, приходящейся на малый элемент ( П - плотность потока мощности падающей волны у цели), после отражения по закону геометрической оптика распределится в телесном угле . Плотность потока мощности рассеянного поля в

окрестности антенны запишется в виде:

Откуда с помощью формулы (1.8) получим выражение (I.I5). Таким образом, ЭПР гладкого выпуклого тела двойной кривизны не зависит от длины волны. Результаты расчета по формуле (I.15) соответствует действительности с ошибкой не более 20% при условии

Найдем ЭПР для шара радиуса р . Уравнение поверхности может быть записано в виде:

Точкой стационарной фазы здесь также будет точка х₀ =у₀ =0 а вторые производные от ΔR равны:

Подстановка этих равенств в формулу (I.I4) определит ЭПР шара:

который равен просто площади его поперечного сечения.

Поясним физический смысл точен стационарной фазы . Так как для них выполняется условие , то это означает, что в этих точках касательная плоскость к поверхности тела будет параллельна плоскости отсчета ММ (рис. I.I), т.е. перпендикулярна направлению распространения волны. Таким образом, основной вклад в поле, рассеянное в направлении на приемную антенну, дают именно эти участия исследуемого тела.

Совсем просто можно рассчитать в рамках рассматриваемого метода ЭПР плоской цели, расположенной перпендикулярно направлению распространения волны. В этом случае и "блестящей" является вся поверхность цели. Поэтому целесообразней непосредственно воспользоваться формулой (I.10). откуда сразу истекает:

формула (I.I7) свидетельствует о возможности несколько иного подхода к расчету ЭПР цели. При рассматриваемом расположении цели, т.е. перпендикулярно вектору Пойтинга, на ее поверхности, кроме узкой об-ласти размером порядка λ у границы, возбуждаются синфазные токи равной амплитуды. Это значит, что цель можно рассматривать как антенну с синфазным равноамплитудным распределением пола (упомянутая выше узкая область около границы особой роли не играет, т.к. принято, что размеры цели существенно больше λ ), коэффициент направленного действия D которой можно вычислить по формуле:

Мощность поля, рассеиваемая идеально проводящей целью, будет равна мощности падающей на него волны (с учетом, естественно, того, что с неравномерностью тока на краях цели можно не считаться), которая, очевидно, будет записываться в виде , а поэтому плотность потока мощности рассеянной волны у антенны с учетом направленных свойств цели будет:

Откуда из равенств (I.I7) и (1.I8) элементарно получается представление (I.17).

Обобщим полученные результаты на случай, когда вектор П_u образует некоторые углы Q и c осями Z и X системы координат, связанной с целью, как это показано на рис. 1.4.

В этом случае фаза тока, наводимого в точке А , будет отставать от соответствующей фазы тока в точке О на величину . Если коэффициенты точки А обозначить черев (x,y) , то:

Что касается амплитуд токов, то в рамках рассматриваемых допущений их надо считать одинаковыми по всей поверхности цели.

Поле в окрестности приемной антенны будет представлять собой сумму элементарных полей, создаваемых элементарными токами, протекающими по поверхности цели, при этом фаза элементарного поля будет равна .

В этом случае по-прежнему будет справедлива формула (I.I9), но под D следует понимать, как это принято в антенной технике, произведение максимального значения коэффициента направленного действия D_max на нормированную диаграмму направленности (по мощности) антенны, имеющей равномерное распределение амплитуд токов и распределение их фаз по закону (1.20), при этом плоский раскрыв такой антенны совпадает с поверхностью цели.

Значение D_max будет определяться формулой (1.18), а нормированная диаграмма направленности определяется как:

Таким образом, c учетом cказанного b соотношений (I.I8) и (1.19) получаем:

т.е. вновь получили формулу (1.10), но в виде, удобном для расчета ЭПР плоских целей.

Соотношения (1.10),(1.I4), (I.I5), (1.17) и (1.21) дают широкие возможности для расчета ЭПР достаточно большого типа целей.

1.2. ЭПР простейших целей

В настоящем разделе будут найдена ЭПР простейших целей, которые не только могут выступать как модели некоторых реальных целей , но и выступать в качестве их составных частей.

I.2.I. ЭПР шара

Задача о рассеянии к дифракции плоской электромагнитной волны на сфере исследована наиболее полно по сравнению со всеми другими телами простой и сложной формы. Особенно велико значение этой задачи для радиолокации, поскольку сфера представляет собой одно из тел простой формы, для которого имеется строгое решение. По этой причине металлические сферы широко используются в качестве эталонов ЭПР. Кроме того, сфера обладает одним уникальным свойством: это единственное тело, рассеивающее энергию во все стороны равномерно. Иными словами, сфера является всенаправленным отражателем как в случае, когда приемная антенна совпадает с передающей (так называемая однопозиционная радиолокация), так и, когда приемная и передающая антенны расположены в разных местах (двухпозиционная радиолокация). Всенаправленность сферы при однопозиционной радиолокации очевидна и не требует пояснений. Что же касается всенапревленности сферы двухпоэиционной радиолокации, то она иногда вызывает недоумение и нуждается в доказательстве, которое приведем в виде , данном в книге В.О.Кобака "Радиолокационные отражатели".

Пусть на идеально проводящую сферу, радиус которой р>>λ, вдоль отрицательного направления оси OZ падает плоская волна а плотностью потока мощности П_u, (рис. 1.5).

Рис. 1.5. К доказательству всенаправленности сферы

Определим плотность потока мощности, рассеянной сферой под углом к направлению падения. Для этого опишем вокруг сферы вторую вспомогательную концентрическую сферу радиуса R₀>>p. Выделим полосу, соответствующую зеркально-отраженным лучам, распространяющимся под углами β и β+dβ. Полюса, как следует из геометрии, будет иметь радиус psin(β/2) и ширину (p/2)dβ . Полная мощность, приходящаяся на полосу, равна - площадь проекцкк поло си на фронт падающей волны.

Энергея после отражения распределится на поверхности второй сферы также по кольцевой полосе, площадь которой при условии равна отсюда находим плотность потока мощности рассеянной волны

Таким образом, действительно плотность потока мощности рассеянной волны не зависит от угла β и является постоянной величиной во всех направлениях. Исключение составляет направление , где приближение геометрической оптики неприменимо.

Что касается численного значения ЭПР, то в случав идеально проводящего шара, радиус которого р много больше длины волны λ. ЭПР шара с достаточно высокой степенью точности может быть рассчитано по формуле (I.I6). Если шар обладает конечной проводимостью, а материал, из которого он сделан, имеет комплексную диэлектрическую проницаемость Е , то достаточно очевидно, что ЭПР по сравнению с предыдущим случаем уменьшатся в коэффициент отражения раз. Строгая теория подтверждает это утверждение, т.е.

Важное значение в радиолокации имеет случай, когда целью является сфера, радиус которой много меньше длины волны, что хорошо моделирует капельки дождя и некоторых искусственных целей. Однако полученные формулы не дают возможности использовать их для этого случая. Дадим без вывода формулы для ЭПР идеально проводящего шара с радиусом р<<λ:

и диэлектрического шара:

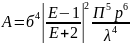
Для капель дождя, когда ,имеет :

.

В области, где имеет порядок 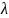или нескольких ,формулы для расчета ЭПР довольно громоздки, поэтому воспользуемся графическим представлением.

На рис. I.6. Приведена зависимость отношения идеально проводящего шара от отношения

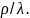
Рис. I.6. Энергетическая функция рассеяния сферы

На Лицо ярко выраженный осцилляционный характер этой зависимости.

Максимум ЭПР имеет место тогда, когда шар становится как бы полуволновым вибратором и вдоль его полуокружности длиной укладывается полуволна тока, т.е. при этом само значение ЭПР более, чем в 3,5 раза превышает площадь поперечного сечения шара. Этим объясняется то, что в сантиметром диапазоне воли при увеличении интенсивности дождя, когда размеры капель воды увеличиваются, просходит резкий рост отражений от дождя, что еще более ярко проявляется в миллиметровом диапазоне.