5.3.6. Мінімізація логічних функцій

Найпоширенішими методами мінімізації є:

1) Метод безпосередніх перетворень;

2) метод карт Карно;

3) метод Квайна.

Гарантовано мінімальний вираз можна отримати лише методом повного перебору в процесі мінімізації всіх можливих варіантів. При багатьох змінних суттєво зростає складність, що приводить до необхідності застосування ЕОМ. Для оцінки складності уводиться поняття ціни реалізації логічної функції, яка за Квайном визначається числом змінних в конституенті, що рівнозначно числу входів логічних елементів, які реалізують дану функцію. Кон’юнкції вищого рангу покриваються кон’юнкціями нижчого рангу, наприклад, , тобто використовується операція склеювання , де а – елементарна кон’юнкція або імпліканта – така логічна функція, яка отримана в результаті склеювання і яка на будь-якому наборі змінних набуває такого самого значення, що й сама функція (конституента), яка її утворила. Якщо в диз’юнкція простих імплікант жодну з них шляхом поглинання визначити неможливо, таку диз’юнкцію називають тупиковою або мінімізованою диз’юнктивно нормальною формою (МДНФ) заданої функції.

Метод безпосередніх перетворень – це аналітичний метод скорочення логічних функцій з допомогою аксіом та законів Булевої алгебри. Досить ефективний для кількості змінних n ≤3.

Корисно пам’ятати:

, .

Приклад: Аналітичним методом мінімізувати логічну функцію .

Рішення:

Інколи простіше мінімізувати інверсію логічної функції для отримання простішого виразу МДНФ (наприклад, за умови, що у виразі функції більше “1”, ніж “0”). Технічно реалізується функція, а потім на виході схеми використовується інвертор.

Метод карт Карно придатний для мінімізації логічних функцій в УДНФ за умови n≤6 і алгоритм мінімізації є таким:

• розміщуються конституенти в клітинках карти Карно, які відповідають мінтермам даної функції, що подана в формі в УДНФ;

• об’єднуються сусідні одиниці контурами по 2, 4, 8 клітинок, причому сусідніми вважаються клітинки, що розташовані на границях карти Карно;

• зчитуються кон’юнкції (імпліканти), що входять у даний контур, вилучаючи з них за законом склеювання ті змінні, які утворюють доповнення ( );

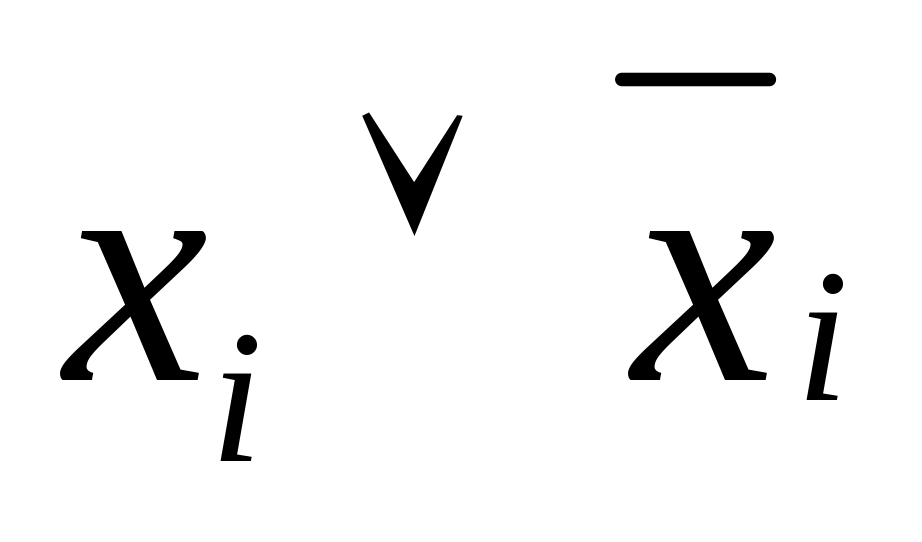• об’єднуються одержані імпліканти диз’юнкцією, яка й і є МДНФ заданої логічної функції.

Наприклад: методом карт Карно мінімізувати логічну функцію (ту ж саму, що й у вище поданому прикладі).

Зчитування з контурів дає такий результат

Метод Квайна – логічна функція повинна бути подана в УДНФ. Мінімізація відбувається за теоремою Квайна.

Таблиця 5.10 – Рішення вищеподаного прикладу методом карт Карно

		X2 X3
X1			X2
			10	11	01	00
	Х1	1	1			1
		0	1		1	1
				X3

Теорема Квайна: якщо в УДНФ виконати всі операції склеювання, а потім – усі операції поглинання, то в результаті буде одержана МДНФ. Необхідно пам’ятати, що склеювання це: , а поглинання -

де а – довільна елементарна кон’юнкція, тобто імпліканта, .

Два етапи мінімізації: 1) одержання скороченої ДНФ; 2) отримання МДНФ на основі скороченої ДНФ.

Методика мінімізації подана на прикладі (тому самому, що й поданий вище). Цей метод універсальний. Застосовується на ЕОМ.

За методом Квайна мінімізувати логічну функцію:

.

Підбір імплікантних пар, що склеюються у виразі логічної функції: (1-2): ; (1-5): ; (2-4): ; (3-4): ; (4-5): (табл. 5.11).

В табл. 5.11 можна викреслити середній стовпець з мінімальною (одиничною) кількістю позначень, а, відповідно, й передостанній рядок з таблиці 5.11, де знаходиться дана позначка, то й імпліканта є базовою і результат зчитування з першої імплікантної таблиці: .

Підбір імплікантних пар, що склеюються у виразі частково мінімізованої логічної функції: (1-4): ; (2-3): . З другої імплікантної таблиці (табл. 5.12), видно, що імпліканта входить у всі стовпці без винятку, тому вона й і є базовою. Остаточно, результат мінімізації за методом Квайна можна зчитати з обох таблиць (табл. 5.11, табл. 5.12) як .

Таблиця 5.11 – Перша імплікантна таблиця процесу мінімізації логічних функцій за методом Квайна

	+	+
	+				+
		+		+
			+	+
				+	+

Таблиця 5.12 – Друга імплікантна таблиця процесу мінімізації логічних функцій за методом Квайна

	+	+	+	+

Отже, підсумовуючи результати мінімізації за різноманітними методами (див. приклади), робимо висновок, що результат є однаковим для усіх трьох використаних методів.