5.1.2. Перевід чисел з однієї системи числення в іншу

Алгоритм: ділення числа А_р на основу р системи, в яку переводиться число:

1. Ділення в цілих числах числа А_р на основу р тієї системи, в яку переводиться число А_р;

2. Якщо частка 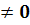, вона береться за нове число і повторює операції п. 1; якщо частка =0, то перейти до п.3

У загальному випадку дробова частина числа переводиться шляхом підбору ваг розрядів основи нової системи числення так, щоб вони завжди були не більшими від неї. При цьому задається точність результату переводу, яка зазвичай дорівнює половині одиниці молодшого розряду вихідного числа.

ПРИКЛАД 1.1: число 123,321₁₀ перевести у двійкову систему числення

123 | 2__

-122 _61 | 2__

1 60 30 |2__

МБ 1 -30 15 | 2

0 -14 7 |2__

1 -6 3 |2__

1 -2 1

1 СБ

123₁₀=1111011₂

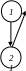
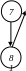
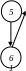
Д ля переводу у двійкову систему дробову частину слід послідовно домножувати на число 2. Двійкове число записується у вигляді цілих частин чисел, які отримані при перемноженні тільки дробової частини, починаючи зверху після коми. Тут точність +0,0005≤2^-11

0 ,321 0,284 0,136 0,544 0,176 0,704

× ___2 ×___2 ×___2 ×___2 ×____2 ×___ 2

С Б - 0,642 0,568 0,272 1,088 0,352 1,408

×___2 ×___2 ×___2 ×____2 ×___2 МБ

1,284 1,136 0,544 0,176 0,704

ПРИКЛАД 1.2: двійкове число 1111011,01010010001₂ перевести в десяткову систему числення.

Для цього записуємо двійкове число через відповідні ваги двійкових розрядів та підсумовуємо їх і отримуємо десяткове число

1111011,010100100012=2⁶+2⁵+2⁴+2³+2¹+2⁰+2^-2+2^-4+2^-7+2^-11=64+32+16+8+2+1+ +0,25+0,0625+0,0078+0,002=123,3208 123,321

Спрощений перевід: 2

111 1 - МБ

. 55 1

27 1

13 1

6 0

3 1

1 1 – СБ 2⁶+2⁵+2³+2²+2¹+2⁰=111

=100...0 =11…1

m нулів m одиниць

Приклади спрощених розрахунків:

69₁₀=64+5=2⁶+101₂=100000+101₂=1000101₂

31₁₀=32-1=2⁵-1=11111

ПРИКЛАД 1.3: десяткові числа 123₁₀ та 1727₁₀ перевести у шістнадцятковий код

1 23 16 1727 16

-112 7 - СБ -16 107 16

11 - МБ 127 -96 6 - СБ

-112 11

15 - МБ

123₁₀=7В₁₆ 1727₁₀=6BF₁₆

ПРИКЛАД 1.4: шістнадцяткові числа 7В₁₆ та 6BF₁₆ перевести в десяткову систему числення.

7×16¹+11×16⁰=123₁₀; 6×16²+11×16¹+15×16⁰=1536+176+15

5.2. Принцип дії основних типів логічних елементів

5.2.1. Транзисторний ключ – основа схемотехніки логічних елементів

Транзисторний ключ - основи цифрових елементів (рис.5.1).

Транзистори – біполярні, польові з р-n переходом, польові з ізольованим затвором.

Логіка – додатня, від’ємна.

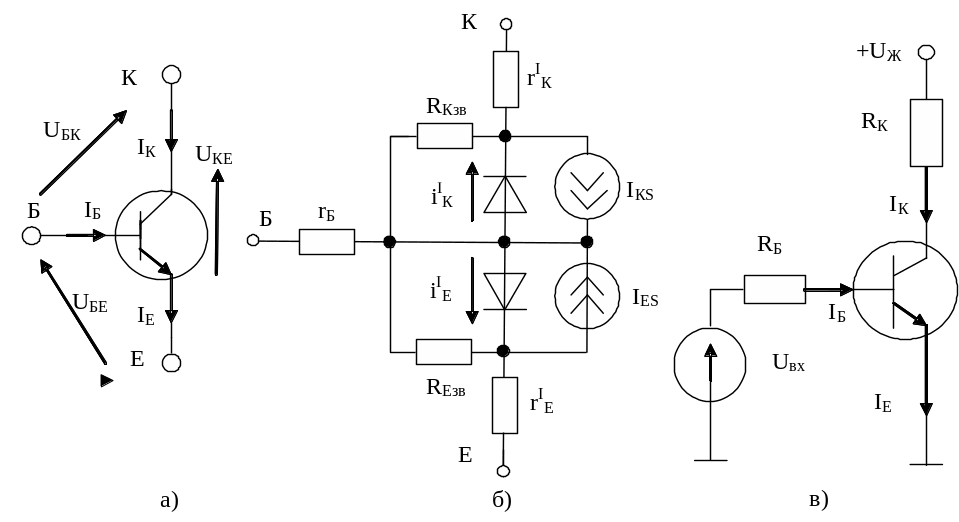
Рис. 5.1 – Позначення n-p-n транзистора (а), його заступна схема (б) та схема найпростішого транзисторного ключа

І_КS, I_ЕS – струми неосновних носіїв; , - відповідно, опори бази та емітера; R_Кзв, R_Езв - опори ізоляції, відповідно, колекторного та емітерного переходів; - інжекційні струми, відповідно, емітера та колектора.

В статичному режимі можна записати: , де α, α_І – коефіцієнти передавання емітерного струму в колектор та колекторного струму в емітер (для сучасних транзисторів їх значення знаходяться у межах α, α_І≈1; 1-α=0,05…0,001; 1-α_І=0,2…0,01/

Математична модель транзистора - рівняння Еберса – Молла (рис. 5.2)

,

,

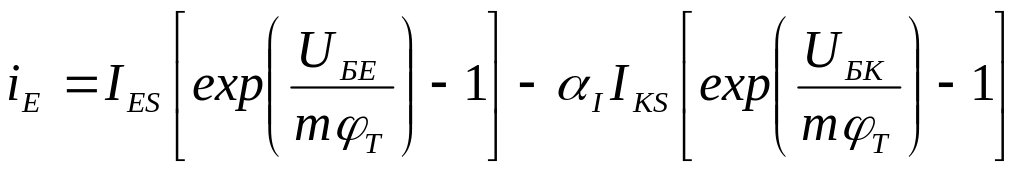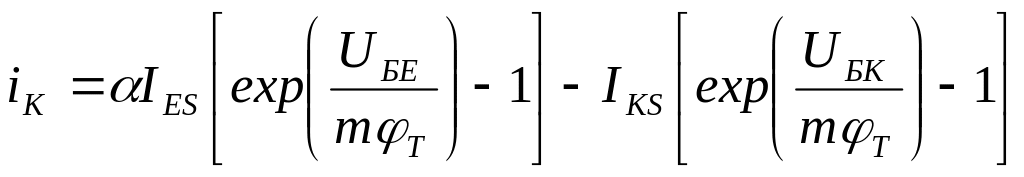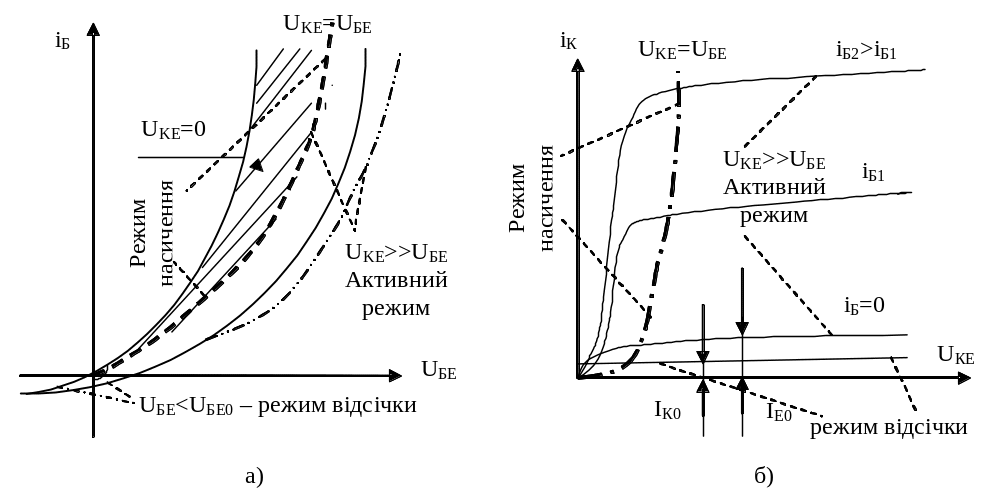
Рис. 5.2 – Вхідна (а) та вихідна (б) характеристики біполярних транзисторів для різних режимів роботи

,

.

; .

Режим відсічки: U_БЕ 0; _UКЕ >0 (n-p-n транзистор)

_{іК=ІКБ0; іЕ=UЕБ/RЕзв; іБ= ІКБ0+ UЕБ/RЕзв.}

Активний режим: U_БЕ > U_БЕпор>0; U_КЕ > U_БЕ>0_;

U_БЕ=mφ_Т·ln(-і_К/І_ЕS); і_К=βі_Б+І_КЕ0(1-е^(U_БЕ^-U_КЕ^)/mφ_T⁾.

Режим насичення: U_БЕ > U_БЕпор>0; U_КЕ≤U_БЕ

Умова насичення : і_Б≥і_К/β; β=α/(1-α);

;

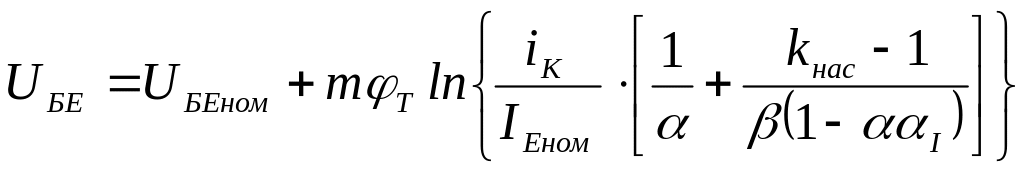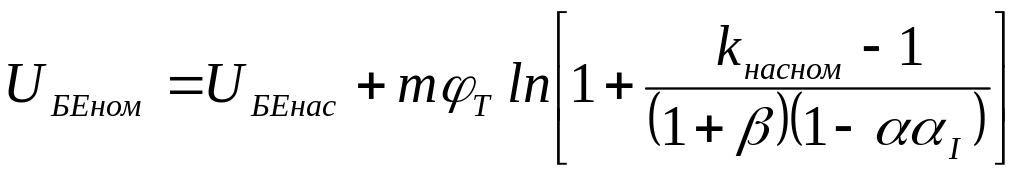; ; - інверсний коефіцієнт передавання струму.

Рівняння робочої точки на вихідній характеристиці U_КЕ=U_ж-і_КR_К

Насичення: І_Кнас≈І_Кз=Е_К/R_К за умови U_КЕ<< Е_К.

Відсічка: U_КЕ≈ Е_К.