4.1.1. Похибка від зміни сигналу протягом перетворення

Теоретично неможливо отримати результат вимірювання за нескінченно короткий інтервал часу, тому що при скінченній енергії була би нескінченно великою відібрана з вимірювального сигналу потужність. Як і в аналогових ЗВТ, цифрові характеризують імпульсною функцією, яка при аналого-цифровому перетворенні приймається скінченною в часі і вона власне визначає його тривалість. В багатьох випадках результат аналого-цифрового перетворення пропорційний до середнього значення сигналу. Для зменшення впливу зміни сигналу протягом аналого-цифрового перетворення на вході швидкодіючого АЦП використовують так званий пристрій вибірки та зберігання, що функціонує, наприклад, на принципі короткотривалого під’єднання вхідного сигналу до конденсатора, його швидкого заряду і подальшого від’єднання вхідного сигналу. Запам’ятоване в такий спосіб значення величини (вибірка) втримується на виході цього пристрою так довго, як це потрібно для наступного аналого-цифрового перетворення. Очевидно, що в АЦП з пристроєм вибірки-зберігання хоча протягом дуже короткого інтервалу часу – часу заряду конденсатора, усе ж відбувається усереднення сигналу. Результат перетворення усереднюючих АЦП (з часовим чи частотним перетворенням), відповідно до принципу їх роботи, дорівнює середньому значенню сигналу.

Тому загалом можна прийняти, що значення вибірки сигналу в момент часу t_i є її середнє значення протягом часу відбирання вибірки чи перетворення T_a/ц

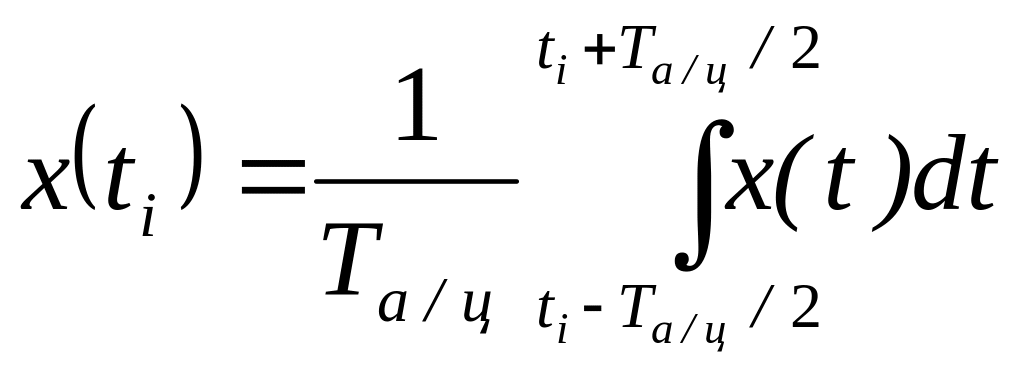. (4.3)

Похибка від такого усереднення залежить від часу усереднення T_a/ц і від характеру зміни сигналу. Так при лінійному наростанні сигналу вона дорівнює нулю. При аналого-цифровому перетворенні змінного сигналу амплітудою x_м і частотою  усереднення спричиняє зміну амплітуди тобто відносну амплітудну похибку

, (4.4)

де f_а/ц= (T_а/ц)^-1 – частота перетворення АЦП. Похибка від’ємна оскільки амплітуда усередненого сигналу є меншою за амплітуду вхідного.

Приклад. Якщо час перетворення АЦП T_а/ц=50 мкс, то при перетворенні сигналу з максимальною частотою f = 1 кГц, максимальна похибка від усереднення сигналу може бути значною. Тому слід обґрунтовано, враховуючи апріорну інформацію про властивості сигналу, вибирати швидкодію АЦП.

Квантування за рівнем вимірюваної величини Х полягає у визначенні квантованого і заокругленого в результаті квантування значення даної величини

х_кв=N_xq, (4.5)

де N_xq – квантовий (дозволений) рівень, до якого заокруглюється значення вимірюваної величини; N_x – числове значення; q – крок квантування (різниця між сусідніми рівнями квантування).

Як наслідок цього, цифровий результат містить похибку заокруглення, яку стосовно фізичних величин (а також внаслідок певних відмінностей заокруглення від загально прийнятих в математиці) називають похибкою квантування. Отже, похибка квантування – це різниця між заокругленим результатом вимірювання та справжнім значенням вимірюваної величини (рис. 4.3)

_кв = х_кв – Х = N_xq – X. (4.6)

Спосіб заокруглення до квантового рівня значною мірою визначається технічною реалізацією АЦП. Для різних значень вимірюваної величини похибка квантування змінюється періодично, у 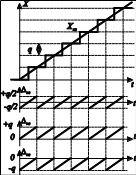вигляді зубців пили (рис. 4.3). Використовують заокруглення до ближчого рівня (рис. 4.3,а), більшого рівня (рис. 4.3,б) чи меншого рівня (рис. 4.3,в). При заокругленні до ближчого квантового рівня (рис. 4.3,а) похибка квантування не перевищує половини кроку квантування _кв   q / 2, а при заокругленні до більшого чи меншого рівнів вона може досягати розміру кванту з різним знаком.

О

Рис. 4.3. До похибки квантування

станній (молодший) розряд заокругленого результату вимірювання не обов’язково мусить змінюватися через десяткову одиницю, як це є зазвичай в математиці. На практиці молодший розряд в певних випадках може набувати лише парних значень (тобто результат вимірювання закінчується цифрами 0; 2; 4; 6; 8) або набувати значення через 5 (тобто закінчуватися цифрами 0 та 5).

Із збільшенням номінального значення ступенів квантування N_н та із зменшенням тривалості циклу дискретизації Т_ц складність і вартість ЦВП суттєво зростають. Тому кількість ступенів квантування N_н та тривалість циклу дискретизації слід вибирати за заданими значеннями похибки вимірювання і швидкодії. На сучасному етапі складність і вартість ЦВП може бути суттєво знижена використанням малогабаритних та порівняно недорогих інтегральних АЦП.

Кодування результату аналого-цифрового перетворення – це операція його представлення за допомогою сукупності (кодових) символів вибраного алфавіту (системи числення), що здійснюється за однозначними правилами. При цьому пере­важно використовується числове кодування і для цифрових вимірювань це є операція переводу числового значення даної величини N_x в іншу систему числення. Незалежно від використовуваної системи числення, результати перетворення АЦП переважно представляються бінарними символами, тобто лише двома різними рівнями.

Крім безпосереднього кодування результатів аналого-цифрового перетворення, у вимірювальній техніці кодування використовується також у пристроях відображення результатів, а також з метою отримання певного рівня завадостійкості при передачі результатів каналами зв’язку.

Кожен закодований результат зображується певною кількістю кодових символів або кодовою комбінацією, яка відповідає правилам використовуваного коду. При цьому існують різні системи кодування, які, однак, використовують одні і ті ж кодові символи.

Цифровим кодом називається сукупність правил, які встановлюють значення кожного елемента залежно від його місця в кодовій комбінації та її довжини. У вимірювальній техніці найчастіше використовується такі цифрові коди, як одиничний нормальний, одиничний позиційний, двійковий нормальний, ціла група двійково-десяткових кодів, код Грея (в АЦП з перетворенням просторових (кутове чи лінійне положення) параметрів), та інші, які зручні для реалізації різноманітними цифровими пристроями.

Одиничний нормальний (число-імпульсний) код – значення числа подається кількістю імпульсів.

Одиничний позиційний код – значення числа подається положенням одиниці серед нулів.

Таблиця 4.1 - Цифрові символи первинних цифрових кодів загального використання

Десят­ко­ве число	Одиничний нормальний код	Одиничний позиційний код	Двійковий нормальний код	Двійково-десятковий код
0	1	0000000000	00000	0000 0001
1	11	0000000001	00001	0000 0010
2	111	0000000010	00010	0000 0011
3	1111	0000000100	00011	0000 0100
4	11111	0000001000	00100	0000 0101
5	111111	0000010000	00101	0000 0110
6	1111111	0000100000	00110	0000 0111
7	11111111	0001000000	00111	0000 1000
8	111111111	0010000000	01000	0000 1001
9	1111111111	0100000000	01001	0000 1010
10	11111111111	1000000000	01010	0001 0000

Десятковий код (основою є число 10) – значення числа подається у десятковій системі числення цифрами від 0 до 9 з вагами, пропорційними 10 у відповідному степені, наприклад, 733 = 710² + 310¹ + 310⁰.

Двійковий нормальний код (основою є число 2) – значення числа подається у двійковій системі числення послідовністю n двійкових цифр а_n-1а_n-2 а₂а₁а₀, кожна з яких може мати лише значення а_і=0 та 1, наприклад, 10011101, при цьому вага цифри у числі дорівнює числу два у степені, яка визначається номером (позиції) розряду .

Наприклад, у випадку 8 розрядного двійкового числа 10011101 його десяткове значення

N_x = a₇2⁷ + a₆2⁶ + a₅2⁵ + a₄2⁴ + a₃2³ + a₂2² + a₁2¹ + a₀2⁰ =1·128+0·64+0·32+1·16+1·8+1·4+0·2+1·1=157.

Двійково-десятковий код – кожна цифра (розряд) десяткового числа подається двійковим кодом (використовується 4 двійкові розряди – тетрада, а кількість тетрад дорівнює кількості десяткових розрядів числа).

Крім двійкового нормального, використовуються також двійковий інверсний, доповняльний та інші види кодів. Двійково-десяткові коди у межах тетради можуть мати не тільки двійкові ваги 8421, а й інші, наприклад, 4221, 2421, 5211 тощо. Використовуються також коди Грея, Джонсона, вісімковий та шістнадцятковий.

Зміщений двійковий код утворюється введенням додаткового старшого розряду, запис в яких активного одиничного рівня означає додатне число, а запис нуля – від’ємне.

Доповняльний код буває двох типів – прямий та зворотний. Прямий з допов­нен­ням до двох має однакові зі зміщеним кодом стани вагових розрядів. Проте додатні числа кодуються нулем у старшому розряді, а від’ємні – одиницею. Нормалізовані додатні числа утворюються підсумовуванням вагових коефіцієнтів розрядів, а від’ємні – підсумовуванням вагових коефіцієнтів з мінус одиницею. Зворотний з доповненням до двох код має подвійне відтворення нуля. Для додатних чисел подання в доповнювальному та зворотному кодах збігається з поданням у прямому. Подання від’ємних чисел відповідає інверсному коду додатних чисел у прямому коді зі знаком.